基于三元闭包的不确定社交网络隐私保护算法∗

彭擎宇 文中华，2 原伟杰

（1.湘潭大学计算机学院网络信息安全学院 湘潭 411105）（2.海南热带海洋学院计算机科学与技术学院 三亚572022）（3.湖南工程学院计算机与通信学院 湘潭 411104）

1 引言

随着互联网技术的飞速发展，第五代移动通讯技术（简称5G 技术）的不断发展［1］，越来越多的人投入到社交网络中进行交流并共享信息。例如：2016 年Facebook 每月拥有14 亿用户，拥有9 亿每日活跃用户［2］。随着时间的增加社交网络中累计了大量的用户数据，大部分用户的身份信息，社会关系信息等敏感信息将被发布到网络中，这些信息都会成为攻击者的攻击目标，所以在发布社交网络数据时保证个人的匿名性是一个具有挑战性的研究问题。迄今为止提出的匿名化社会图的方法大概可分为3 大类：1）k度匿名保护模型，该模型将顶点分组为至少k个大小的超级顶点，使目标的隐私泄露的可能性<1/k，其中k是所需的匿名水平；2）通过随机添加、删除或切换边缘的形式向数据添加噪声的方法，从而使攻击者不能够依靠背景知识准确地识别原始图结构的方法；3）通过向原始图注入不确定性生成不确定图，改变图属性的方法。目前在计算机科学、工业科学、社会科学、自然科学、生物科学等众多研究领域都存在着不同程度的不确定性［3］。

根据以上三类不同的研究学者提出了不同的研究方法，例如：Fard 等提出的一种邻居随机的边扰动方法［4］；P.L.Lekshmy 等提出的加快隐私保护内核K均值聚类的混合保护方法［5］；Varsha提出的在保留隐私的情况下识别社交网络中的传播者［6］；Nguyen 等在提出一种不确定隐私保护方法通过方差最大化的方法来衡量隐私与效用之间的联系［7］；以上研究方法主要针对静态社会网络，而对处于动态变化中的社交网络适用性不好。另外，这些隐私保护方法在着重于加大图的隐私性保护程度的时候对图数据效用的破坏程度较高。

三元闭包原则是一个社交网络中的基本原则：在同一个社交网络中，如果两个人之间有一个共同的朋友，那么这两个人在未来成为朋友的可能性就会提升。根据三元闭包的基本原则，众多研究者把它作为社交网络中推荐算法和重要的链接生成算法的基础。Giuliana等在研究Twitter的社交网络的时候，使用了HIT 算法得到了朋友的推荐结果并且产生了不错的效果［8］。Peng 等通过引文网络中的引文链接的生成，证明了三元闭包方法是多种网络生成新链接的重要原则［9］。Bianconi等以社交网络节点数和聚集度为基础建立了简单的社交网络模型，该模型可以自然导致社区出现［10］。这些研究说明了三元闭包方法可以一定程度的预测社交网络生长结果。

针对上述问题，本文提出一种基于三元闭包的不确定图的社会网络隐私保护方法，主要贡献是：1）考虑到社交网络本身存在的动态性，本文使用了三元闭包方法生成潜在边，更好地反映真实的社交网络环境，有效地保护了社交网络隐私。2）对含有潜在边的社会网络图使用(k,ε)-模糊方法注入不确定性，在保持原图高效用的情况下对原图提供有效的保护。

2 相关定义

定义1：对于给定无向图G=(V,E)，其中V是顶点集，E是边集。我们使用Vp表示边集V中的所有无序顶点对，即Vp={(vi,vj} |1 ≤i≤j≤1}。

定义2：对于给定图G，如果存在映射p:Vp→[0,1]是每条边存在的概率函数，则G'=(V,p)是关于G的不确定图。

定义3：（潜在边）根据三元闭包原则：如果两个人有共同的朋友，这两个人将来成为朋友的概率就会增加。在原始社交网络中如果节点A与节点B具有共同的朋友C，则节点A与B间存在潜在边。

定义4：不确定图G’ 诱导了一个可能世界W(G') ，W∊W(G') 是 一 个 图W=(V,EW)，其 中EW⊆EC，则不确定图G’中的边的概率表明W的概率为

其中，EW为引入不确定性的顶点集合，p(e)为边存在的概率，且不确定图中不同的边的概率分布是相互独立的。

定义5：给定一个不确定图G'，假定攻击者知道他的目标顶点和一些顶点的性质P，令Ωp为P取值的域。当P 代表的是所有顶点的度的时，Ωp={0 ,…,n-1} 。则对每个vϵG'并且w∊Ωp，顶点vϵG并且具有属性P的概率为

其中Pr(W)由式（1）中给出，χv,w(W)是一个0-1 变量，它指示顶点v是否在可能的世界W中具有w的属性值。同样，图G中具有属性值w的顶点v在G’中像的概率Yw(v)为

定义6：(k,ε)-模糊处理（以后都称(k,ε)-模糊），如果P为顶点性质，k≥1 是所需要的模糊水平，ε≥0 是一个容许参数。当G’的顶点分布熵大于或者等于log2k时，不确定图G’就可以被称为关于属性P在v∊G的k-模糊，即：

定义7：如果对于v∊G'并且令e1,…,en-1是包含顶点v的n-1 个顶点对，那么对于每一个1 ≤i≤n-1，ei是一个随机的伯努利变量，dv是v的度所对应的随机变量，则有：

那么对于v的每一个可能的度w∊Ωp，都有：

如果式（5）中含有大量的加法，我们可以用高斯分布近似的表示dv，如下所示：

定义8：如果P 是图G 在顶点集合V 上的一个属性，P:V→Ωp，并且参数θ>0，对于任意属性值w∊Ωp，则有属性值w的θ-共性Cθ(w)和θ-唯一性Uθ(w)分别为

定义9：为了使不确定图G'能够更好地保持原始图G的特性，设置了一个[0 ,1] 截断的高斯分布。

3 相关算法

3.1 基于三元闭包的潜在边算法

对于一个社交网络图GY=(V,EY)，其中V为顶点集，EY为边集。我们对GY进行加边处理后可得到图G，如图1所示。

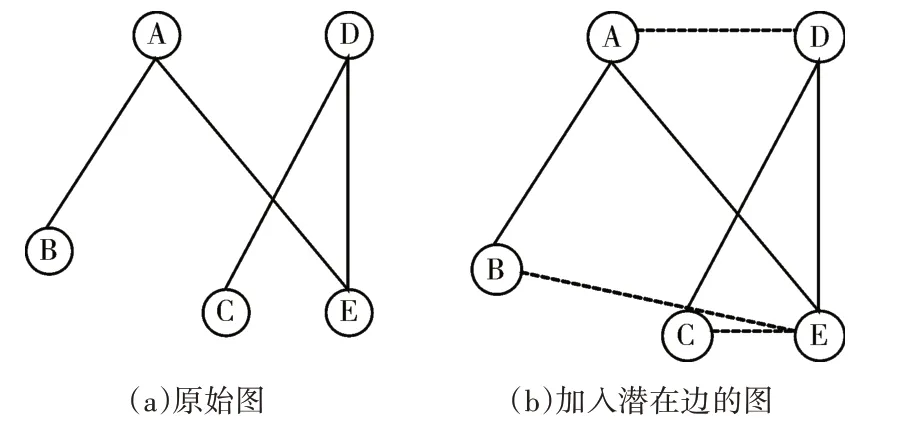
图1 原始图和加入潜在边的图

相关算法如下：

算法1：潜在边算法

输入：初始图GY=(V,EY)，节点集为V，边集为EY，需求添加的边数ex；

输出：加入潜在边的新图G=(V,E)，新边集E。

1：E←∅,i=0

2：WHILEi

3：RANDOMLY PICK A PAIR OF VERTICESu,v，AND (u,v)∉EY，dis(u,v)=2

4：EY←EY∪(u,v)

5：i=i+1

6：E←EY

7：RETURNG=(V,E)，E

原图经过处理后，通过加入潜在边可以使部分顶点的某些属性P发生改变，实现部分隐私保护的效果。例如，某些文献都认为攻击者知道目标顶点的某些性质P［12~15］，比如知道顶点的度、顶点及其邻域的度。

3.2 使用(k,ε)-模糊算法对图G 进行模糊处理

算法2 的目的是找到可以往图G中注入最小不确定性又可以符合条件的(k,ε)-模糊的不确定图，算法3是算法2的子算法，在给定不确定性的参数σ的条件下，找到图G的(k,ε)-模糊图。

算法2：(k,ε)-模糊算法

输入：G=(V,E)，顶点属性P，模糊等级k，容许参数ε，尺寸乘子c，以及白噪声水平q；

输出：G关于属性P是(k,ε)-模糊的不确定图G'F。

1：σι←0

2：σu←1

3：REPEAT

4：<ε',G'>←obfuse(G,σu,P,k,ε,c,q)

5：IFε'=∞THENσu←2σu

6：UNTILEε'≠∞

7：G'F←G'

8：WHILEσl+σ<σudo

9：σ←(σu+σl)/2

10：<ε',G'>←obfuse(G,σu,P,k,ε,c,q)

11：IFε'=∞THENσl←σ

12：ELSEG'F←G'；σu←σ

13：RETURNG'F

算法2 是图G关于顶点性质P的(k,ε)-模糊算法，旨在通过对不确定参数σ的调整，注入最小的不确定性，达到较高的实用性，实现所需要的模糊效果。

算法3：子算法obfuse算法

输入：G=(V,E),P,k,ε,c,q以及标准差σ；

输出：<ε',G'>，其中G’是一个在ε'<ε时的(k,ε')-模糊或在ε'=∞时(k,ε')-模糊不成立。

1：FOR ALLv∊VCOMPUTE THEσ-uniquenessUσ(P(v))

2：H←THE SET OF

|VERTICES WITH LARGESTUσ(P(v))

3：FOR ALL

4：ε'←∞

5：FORtTIMES DO

6：EC←E

7：REPEAT

8：RANDOMLY PICK A VERTEXu∊VHACCORDING TOQ

9：RANDOMLY PICK A VERTEXv∊VHACCORDING TOQ

10：if(u,v) ∊E THEN EC←EC{(u,v)}

11：ELSEEC←EC∪{(u,v)}

12：UNTILE |EC| =c|E|

13：FOR ALLe∊ECDO

14：COMPUTEσ(e)

15：DRAWwUNIFORMLY AT RANDOM FROM [0,1]

16：ifw

17：THEN DRAWreUNIFORMLY AT RANDOM FROM [0,1]

18：ELSE DRAWreFROM THE RANDOM DISTRIBUTIONRσ(e)

19：IFe∊ETHENp(e)←1-reELSEp(e)←re

20：ε''←|{v∊V:not k-obfuscated by G''=(V,p)| |V|

21：IFε''<ε'and ε''<εTHENε'←ε''；G'←G''

22：RETURN <ε',G'>

子算法obfuse算法在给定的标准差参数σ的条件下找出图G的(k,ε)-模糊图G'。首先，该算法计算了每个顶点v∊V的σ-唯一性级别Uσ(P(v))。然后，第14 行将根据顶点唯一性的不同，重新分配的所有顶点对e∊Ec的唯一性级别将按下式分配。

最后，通过给定边的不确定水平σ(e)，为每个顶点对e∊Ec选择一个随机扰动re（定义9），得到(k,ε)-模糊图G'。

4 实验结果

由于不同的隐私方法在评价隐私保护效果时方法有差别，本文将采用边熵来度量不同隐私保护算法的隐私性；采用文献［16］中提供的统计方法度量生成的不确定图的数据效用性。

4.1 隐私性度量

定义10：不确定社交网络图中，边的不确定程度越高，不确定方法对原始社交网络的保护越好。即边熵Ente的值越高图的隐私性越强。

其中，e∊G'，p(ei)该边存在的概率，Ente为不确定图的边熵。

4.2 数据效用性度量

定义11：我们用d1,…,dn来表示图GY中的度序列。如果对于函数F，有S=F(d1,…,dn)，则称S为基于度的统计量。

根据定义11：我们可推理如下统计量：

边的个数（Number of edges）：

节点的平均度（Average degree）：

度方差（Degree variance）：

当图G'是一个不确定图时，d1,…,dn将是随机变量。如果F是线性函数则我们能推出：

4.3 实验结果及隐私性对比分析

本次实验中我们选用了斯坦福大学公开的三个大型网络数据集，Facebook、Twitch和Github。

表1 为潜在边算法的实验结果，通过对原图加入潜在边，然后使用(k,ε)-模糊算法注入不确定性达到隐私保护的目的。从表1 中可看出随着潜在边的增加，得到的不确定图的边熵也在明显增加。

表1 潜在边算法的边熵变化

表2 是使用差分隐私法得到的实验结果，从表2 可以看出随着节点数量的增加，边熵也在明显的增加。但是在不同的隐私预算的情况下，边熵的变化并不明显。

表2 差分隐私法的边熵变化

根据表3 可以看出，随着加边数量的增加，潜在边算法的数据效用逐渐降低。而差分隐私算法的数据效用明显弱于潜在边算法。

表3 两种算法的数据效用比较图

我们从三张表可以看出，差分隐私算法虽然有较高高的隐私性，但是数据效用太低，常用的隐私网络不需要这么高的隐私性，而且差分隐私法对原始图的破坏程度较大，适用范围较为有限。而潜在边算法在保持较好的隐私性的同时，数据效用极好，在用于社交数据挖掘和分析的时候能起到更好的效果。另外我们可以通过调整加入的边ex的大小，和模糊程度k的大小来获得我们所需要的隐私保护程度与数据效用，对不同的真实社交网络达到不同的保护效果。同时，所加入的潜在边为对真实社交网络又有一定的预测性，所以在真实社交网络发生变化时也具有一定的隐私保护能力，具有一定的动态性。

5 结语

本文介绍了一种新的社交网络的隐私保护方法，该方法通过向原始网络中加入一些预测边，来适用社交网络的动态变化，然后对修改后的图注入不确定性形成不确定图，从而达到隐私保护的目的。该方法相对其他不确定的隐私保护方法，适用范围较广，可以在不同环境中动态调整隐私保护程度。后续工作是提升对动态社会网络的适用性，使所加入的潜在边能够更加精准地预测社交网络的动态变化情况。