基于聚类-LSTM 算法的低风速区风速预测∗
陈志昊
(贵州大学机械工程学院 贵阳 550000)
1 引言
随着沿海及西部地区高风速区风资源利用逐渐饱和,低风速区风能开发成为研究的重点[1]。高风速区风向与风速较为稳定,偏航等控制动作较少。低风速区的风况特点为风速较低且风向与风速变化较为频繁,若直接将高风速区的风机控制策略用于低风速区风机,风机偏航等动作控制会出现一定的滞后性,在风向与风速多变时不能及时动作[2]。
为在频繁变化的风况中,使风机的控制获得一定的提前性,需要对风速进行预测[3~4]。文献[5]提出一种基于模拟退火算法改进的深度信念网络短期风速预测算法,并使用自适应学习步长算法进行参数优化,相较于BP 等算法预测精度更高;文献[6]提出一种考虑样本熵的组合分解模式和支持向量回归相结合的预测模型,提高了短期风速预测的准确性;文献[7]提出一种结合集合经验模态分解与样本熵归类算法的长短期记忆组合预测,有效的提升预测精度。本文提出一种基于聚类与LSTM算法的风速预测算法,并针对训练方式提出两种模型,比较传统LSTM算法的训练时间与精度。
2 LSTM预测算法
长短期记忆算法(LSTM)是一种改进的循环神经网络(RNN)。在进行长期依赖学习时,LSTM 能较好地解决RNN 出现的梯度消失或梯度爆炸等问题,实现信息在整个网络中的长期循环[8]。
LSTM 的神经节结构是在RNN 模型上添加了遗忘门、输入门和输出门,通过三个门控制神经节中信息的保留与丢失,其结构如图1所示[9]。
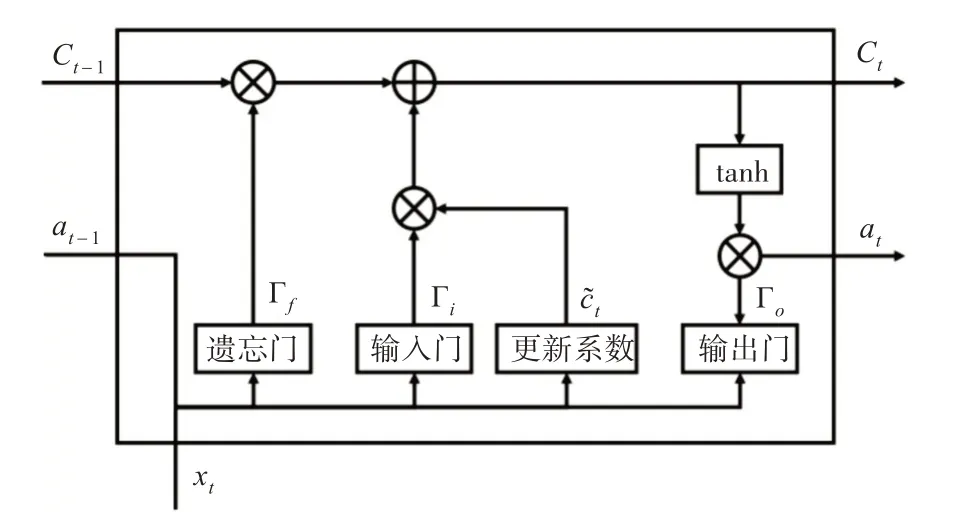
图1 LSTM神经节结构图
当上一神经节的输出at-1与本节的新数据xt输入当前神经节中,会同时进入三个门中。进入遗忘门的数据按式(1)计算出遗系数并对上一神经节传递来的数据Ct-1进行一定遗忘;进入输入门的数据通过式(2)和式(3)更新记忆;遗忘门与输入门输出数据按式(4)计算即获得本神经节的状态Ct;进入输出门的数据按式(5)计算,与本节状态通过式(6)获得本节输出at[10]。
式中,W和b分别为各门的权重与偏置。
LSTM的每一个神经节都会记录当前时序数据的信息,并将信息传递至下一神经节,保证整个时序数据的信息都被记录下[11]。因此,对于风速这一时序数据,使用LSTM 算法对时序数据进行训练时具有一定优势。
在使用LSTM 算法进行预测时,需要使用预测目标点Do前一段时间的时序数据D-t…D-2,D-1作为预测依据数据。t 为预测前数据长度,较长的前数据能为预测提供更多的依据数据。但由于LSTM不断记录时序数据信息的特点,过长的前数据会导致每次训练所累积的数据量过大,进而增大数据存储,同时影响训练时间。
为考量风速预测时前数据长度对预测精度的影响,使用贵州某地全天风速数据在Python上进行训练。该风速数据以1 分钟为采样周期。将前19小时的风速数据作为训练数据归一化后进行预测训练,记录不同前数据长度下的训练时间。并使用剩余风速数据进行预测,计算预测与真实数据间的均方差。结果如图2所示。

图2 前数据长度对预测的影响
从图2 可以看出,当前数据长度较小时,预测均方差较低,预测精度较高。当前数据长度超过60 时,预测均方差较大,预测精度明显降低。且可以看出前数据长度增大时,训练时间也随之增长。当前数据长度为30,即取预测目标前半个小时内的连续数据作为预测依据数据,能获得较好的预测精度,且训练时间较短。
3 基于聚类的LSTM预测算法
3.1 聚类算法
为了提高传统LSTM 算法的预测精度,需要先将原始数据进行处理。由于低风速区风速变化较频繁,考虑将时序风速数据进行分类,使每一类时序风速数据都具有相似变化情况[12]。
K-means 聚类算法是较为常用的分类算法,仅需设定类别数便可进行无监督分类。通过一步步循环,各类初始随机选择的中心会逐渐向目标中心转移,其余数据则不断聚集到距离最近的中心,进而完成数据分类[13~14]。
Calinski-Harabaz(CH)值可以用来表征数据分类的效果,其计算公式为
其中,BGSS为类间平方误差和,计算各类中心与数据总体中心距离的平方和,表征分类后各类间的分离程度;WGSS为类内平方误差和,计算每一类中各点与此类中心距离的平方和,表征各类内的紧密程度。CH值越大,则每一类特征越统一,各类间特征越不同,分类效果越好。
使用前数据长度为30 的时序风速数据进行聚类,选取不同类别数K,在聚类完成后计算CH 值,结果如图3所示。
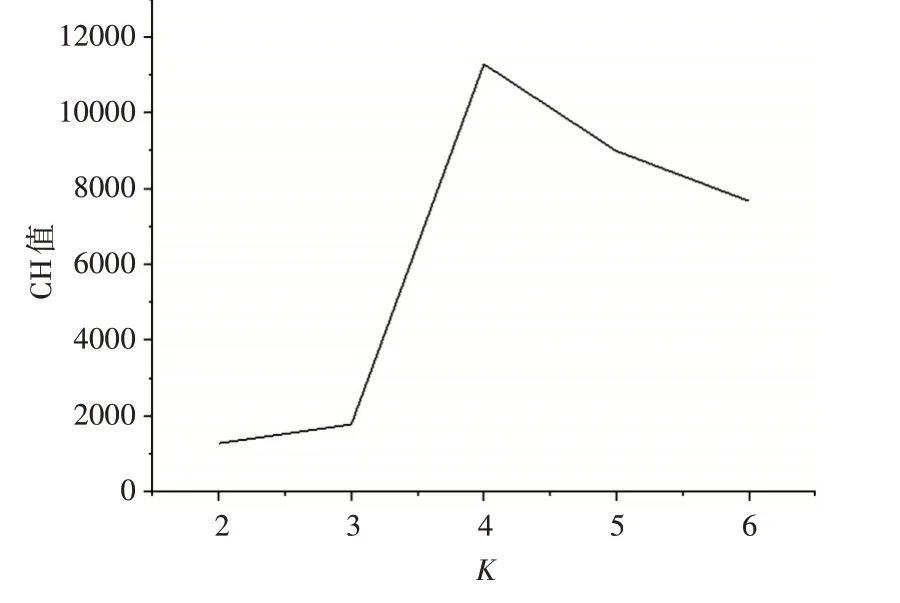
图3 选择不同类别数k下的聚类效果
可以看出,将原风速数据分成4 类的聚类效果最好。因此,选择使用分成4 类的时序风速数据进行预测。
3.2 同一模型训练
原始风速数据在聚类后,分成4 类不同的时序风速数据。将4 类数据放入LSTM 模型中进行训练,在一类输入完成后继续输入下一类数据,即LSTM 模型的训练数据为4 类时序风速数据同类顺次输入训练,原理如图4所示。
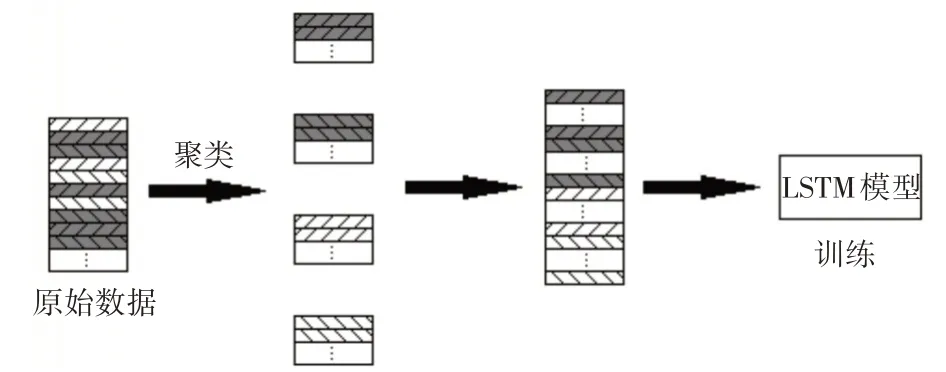
图4 同一模型训练原理图
3.3 分类模型训练
原始风速数据聚类后,将4 类数据分别放入不同的LSTM 模型中进行训练,每一类风速数据都唯一对应一个LSTM模型,原理如图5所示。
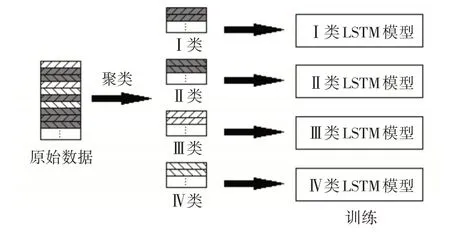
图5 分类模型训练原理图
在完成分类模型的训练后,不能简单地直接进行预测。由于每一类都有对应的LSTM 模型,在预测时需要先将每个数据归类到现有的4 类中,再使用对应的LSTM 模型进行预测。归类方式如下式所示[15]:
式中,d 为需要预测的数据,ck为各类中心。通过计算需要预测的数据与各类中心的距离,将此数据归类到距离最近的类别中。
4 预测结果与分析
使用传统LSTM 预测算法进行训练,并对后5个小时预测得到预测结果与原风速数据如图6 所示。
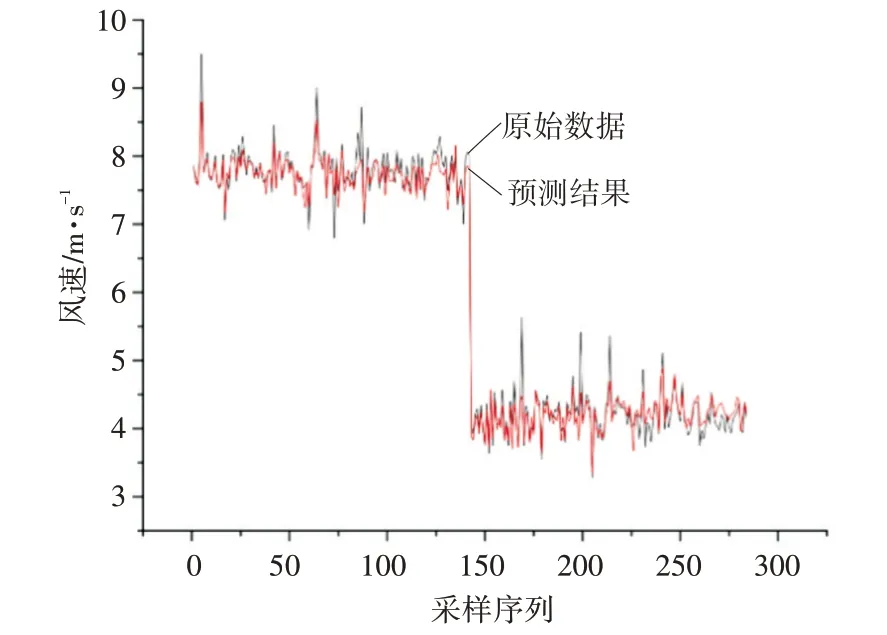
图6 传统LSTM模型预测结果与原风速
从图6 可以看出,预测结果虽能在一定程度上跟随风速的变化趋势,但与原风速数据有较大差距。即使前数据长度较长,使用传统LSTM 算法进行风速预测,预测结果仍不理想。
分别使用上述两种基于聚类-LSTM 的训练方式进行训练与预测,并计算预测结果与原风速数据间的均方差。两种训练方式的预测结果与原风速数据分别如图7、图8所示。

图7 同一模型预测结果与原风速数据
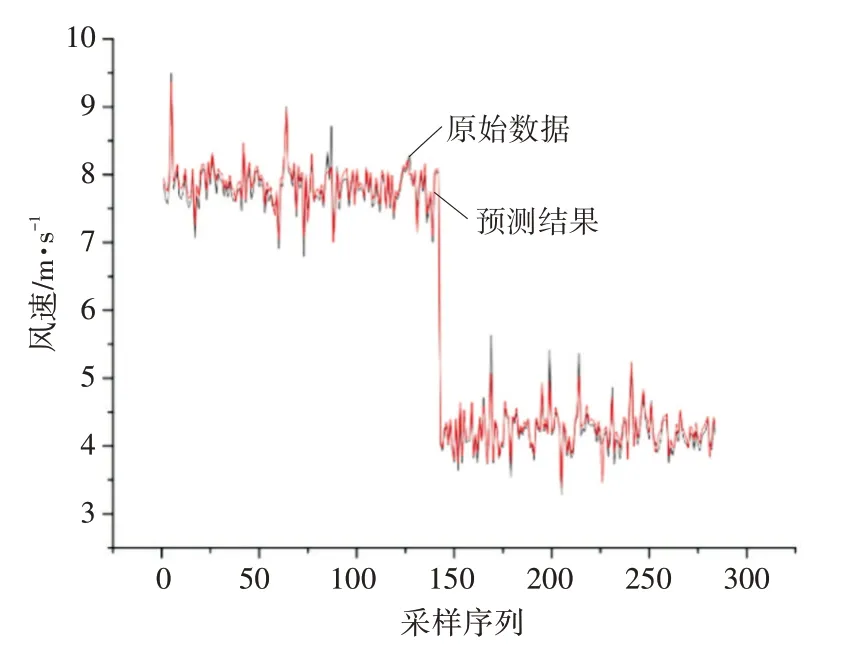
图8 分类模型预测结果与原风速数据
从图7 和图8 可以看出,预测精度相较于传统LSTM 预测算法有明显的提升,预测结果都较为贴近原风速数据。两种模型与传统算法的训练时间与均方差如表1所示。
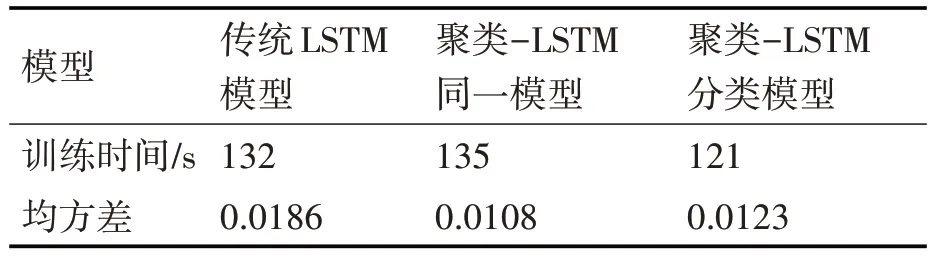
表1 两种组合算法模型与传统算法的训练时间与均方差
从表1 中可以看出,同一模型与分类模型的均方差都显著低于传统LSTM 算法。因此,先进行聚类分类数据处理后再使用LSTM 算法具有更好的预测精度。而相对于同一模型,分类模型的预测精度较低。从图8 中可以看出,在一些风速突变情况下,分类模型能预测变化趋势,但数值上无法很好的贴合原始数据。这可能是由于分类模型中,同样一批训练数据被分配到4 个模型中,每一类对应的LSTM模型仅使用本类的训练数据。相较于同一模型的训练数据,数据量上明显不足。但同一模型与传统LSTM 算法均使用一个模型进行训练,训练时间相近。分类模型使用四个模型进行训练,训练时间有小幅提升。
因此,当基础数据量较大时可以考虑选择使用分类模型进行风速预测,以在更少时间获得较好的预测精度。而当基础数据量较小时,应选择具有更佳预测精度的同一模型。
5 结语
本文提出一种基于聚类-LSTM 的风速预测算法,并提出两种不同的训练模型,与传统LSTM 算法进行对比,结果表明本算法精度有小幅度提升。同时,通过均方差与训练时间得出,基础数据量较小时可以选择同一模型进行训练,而数据量较大时则应选择分类模型。

