半自主自动配置基站算法研究∗

王 俊 杨晓飞 陈进平 冯北镇 王华宇

（江苏科技大学 镇江 212000）

1 引言

GPS 信号［1］属于电磁波，无法穿透钢筋混凝土结构。在这种环境（室内或地下）中很难通过GPS或全球导航卫星系统［2］（GNSS）来定位和导航目标。近年来，基于UWB 的室内定位系统逐渐流行起来。由于UWB 具有抗多径效应的能力，可以结合基于到达时间［3］（TOA）或到达时间差［4］（TDOA）的方法，它可以提供更准确的距离测量信息。通过三边定位法计算，基于UWB 的室内定位系统可以获得比其他更准确的位置信息，例如RSS［5］、信道脉冲响应［6］（CIR）、射频识别［7］（RFID）。许多学者对此进行了综合研究。然而，如何构建基于UWB 和周围环境的室内定位系统以及如何影响系统性能是他们研究的重点。例如，英国的UBisense［8］已成功建立了基于UWB、TDOA和到达角（AOA）的室内定位系统。在Microsoft 室内本地化竞赛中，基于UWB 的各种定位系统已经出现［9］。Guido Schroeder［10］研究了基于UWB 和TDOA 的定位系统。因为在视线良好（LOS）的环境下测距比非视距（NLOS）环境下更加准确［11］。如何检测和识别NLOS 一直是该领域学者关注的重点，这是为了减轻有多径效应引 起 的误差，例如Perz Crus［12］提出可 以 将在NLOS 环境下传播引起的误差视为一个随机变量，并推导出其概率密度函数（PDF）。

Horiba［13］已经通过测量误差的随机特征和改进的迭代最小残差法（IMR）来检测NLOS 的状况。Liu.F［14］提出了一种使用卡尔曼滤波器来整合UWB和IMU数据以提高定位精度的方法。Gao H［15］提出了一种紧密耦合的多传感器融合算法来有效地减少NLOS 和多径干扰，引入模糊校准以自适应地调整对接收到的UWB测量的依赖性。

UWB 的优势在于可以获得更高的定位精度。但是，为了获得目标位置信息，需要安装大量基站，这些基站提供参考位置信息以计算目标位置，多个基站应事先测量坐标，该过程相当耗时且费力［16］。大多数学者仍然通过手动操作分配坐标，如何提高分配效率是一项重要的技术。

2 基站半自主配置方法

在矿井或隧道的两侧可以以一定间隔部署基站。可用于目标定位和跟踪。如图1 所示，基站表示为BSI(i=1,2,3…)。

图1 隧道或矿井中基站的线性网络拓扑

2.1 半自主自动坐标配置策略

半自主自动配置可以通过程序计算大多数基站坐标。在网络中只有两种类型的基站，一种需要通过常规操作测量坐标，另一种需要通过本文算法进行计算。在图2 中，所有基站都固定在隧道的两侧。首先测量网段的前两个基站的坐标，基站的绝对位置信息通常是通过一系列物理方法获得的，例如激光测量或GPS仪器。对于这种网络拓扑，基站的半自主自动坐标计算始于建立一个序列型的虚拟三角形。

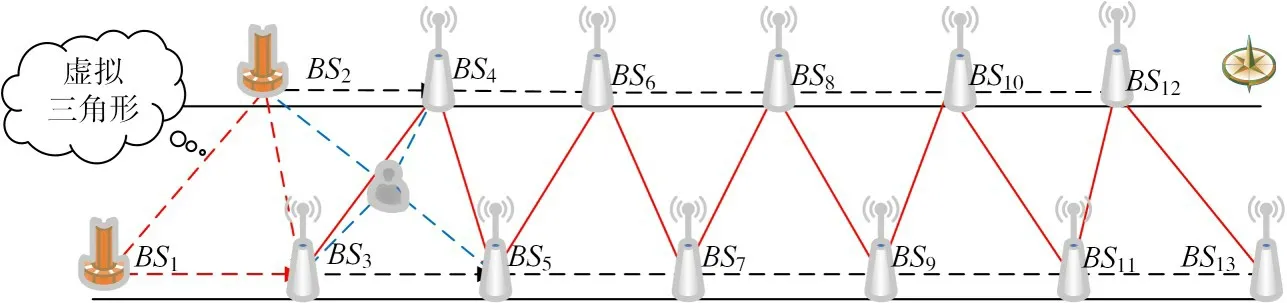
图2 建立虚拟三角形

2.2 虚拟三角形的未校准基站坐标估计算法

假设已经构建了一个虚拟三角形，该三角形具有BS1(x1,y1)，BS2(x2,y2)和BS3的三个顶点。有关如何计算顶点BS3坐标的过程如下：

1）假设BS1和BS2之间，BS1和BS3之间，BS2和BS3之间的距离分别设置为l1、l2和l3，它们可以被测量，如图3所示。

图3 坐标系转换过程

2）将极坐标系转换为笛卡尔坐标系，计算基站的坐标，如图4所示。

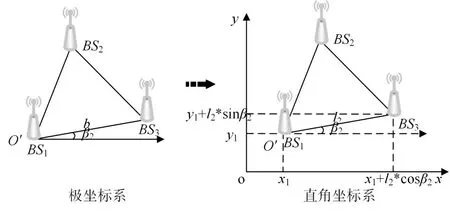
图4 计算虚拟三角形未知顶点的坐标变换

3）通过以上步骤，可以获得虚拟三角形所有顶点坐标。如图5 所示，它们是基站BS1、BS2和BS3。由于已经计算了BS3的坐标，因此可以将其视为新的预校准基站，并且将与原始基站BS2和下一个未知基站BS4形成新的虚拟三角形。然后构建下一个虚拟三角形。开始计算BS4的坐标，这种过程将重复进行，直到计算出所有基站的坐标信息为止。

图5 一段中的虚拟三角形转移过程

图6 标签位置计算过程

3 半自主自动配置技术对定位精度影响的分析算法

在UWB 信号传播和处理期间，将引入误差以引起测距误差。定位的误差累积将随着虚拟三角形传递而增加。基于UWB 的精度有望达到厘米级。一旦误差累积超出此范围，则半自主自动配置算法将被视作失败的。因此，本节将介绍分析半自主自动配置算法对定位精度影响的方法。

根据实际情况应将误差控制到最小，以降低其对定位精度的影响。考虑到误差的累积将随着虚拟三角形转移而增加，因此应讨论布置在一个网段中的基站数量。假设在该段中布置了N个基站，则第i个基站位置是(xi,yi)，需要定位的标签或目标的坐标为(x,y)。目标距离基站距离为li。可以基于测得的TOA(τi)建立方程。

然后，与目标估计位置相对应的误差向量为

其中是对应于目标实际位置的za值。可以使用加权最小二乘［17］（WLS）方法，并且可以使用TOA协方差矩阵Q代替误差的协方差矩阵。

za中的(x,y) 坐标是目标的近似估计位置。假设TOA测量彼此独立，则式（10）中的Q矩阵是对角矩阵，σ是测距误差。

由于za中的L 实际上是与(x,y)相关的量，所以使用Q 矩阵的近似来代替误差矢量的协方差矩阵会导致误差。为了更准确地估计位置，可以使用类似于Chan算法［18］的处理方法。当TOA的误差较小时，对应于TOA测量的N个分位数的误差量为

其中“·”表示Schur 乘积［19］，是目标基站与第i个基站之间的实际范围，而μ是TOA 测量误差，近似遵循正态分布。在式（14）使用TOA 测量结果建立误差向量的协方差矩阵。

其中Q是TOA的协方差矩阵。为了获得B矩阵，可以用测的l1代替l0i，并且za的第一个WLS 估计值是

使用za的值可以获得B的新矩阵。增加这步可以改进估计位置的精确度。

4 基站半自主自动配置算法的仿真与性能讨论

本文已经模拟了半自主自动配置算法，并且分析和讨论了其性能。网络部署如图7 所示，但仅采用一个部分说明。预先校准的基站位于(0,0)和(15,25.982)，其他基站均匀地放置在通道的两侧，间隔约为30m。所有基站之间可以无线通信，信号传输过程中产生的噪声可以被高斯白噪声N(0,0.1)代替。

图7 半自主自动配置技术的坐标系

图8和图9是通过手动和半自主自动配置算法配置基站对定位误差的影响的比较。

图8 X轴上的目标定位误差

图9 Y轴上的目标定位误差

如上所述，本文采用分段方法来确保基站半自主自动配置的准确性。将考虑多个基站分配到一个网段。考虑到UWB技术的定位精度为厘米级［20］，可以将配置精度控制在30cm 以内。通过模拟半自主自动配置算法，当仅向前计算操作时，图10 中第14 个基站和第15 个基站的误差在0.3m 左右波动。这意味着在一个网段中安排的最大基站数量为14最佳。

图10 定位误差超过异常值的最大基站数量

5 结语

本文提出了一种基站的半自主自动坐标配置技术。本文主要贡献是通过参考分割和虚拟三角形两个概念使基站配置过程成为半自主的。本文还讨论在一个网段中分配的基站数量。并且进行仿真以验证算法的性能。仿真结果表明该算法是可行的。