核零空间算法在字符识别中的应用∗

韩 笑 毕 波 唐锦萍 曹 莉

（1.东北石油大学数学与统计学院 大庆 163318）（2.海南医学院公共卫生与全健康国际学院 海口 571199）（3.黑龙江大学数据科学与技术学院 哈尔滨 150080）

1 引言

在当今大数据时代，在很多领域都面临着需要对大量数据进行整理、分类以及异常判别的问题，但是如果利用人力来解决这些问题，无疑非常耗时也耗力，因此利用数据的某些特点来进行分批分类整理以及判别异常无疑是一种更加便捷且高效的方式。

模式识别作为一门新兴的学科，与人工智能和信息科学等学科的发展相辅相成［1~3］。如今，模式识别发展越来越成熟，应用也越来越广泛，遍及机器人、遥感数据分析、生物医学工程等多个领域［4~9］。而字符识别是模式识别中的一个应用，通过训练模型可以教会计算机如何识别字符［10］。通过进行字符识别，不仅可以帮助我们对字符进行整理分类，而且还可以帮助我们从海量的数据中有效检测异常字符。

常用的字符识别方法主要用于利用字符对样本进行整理分类，常用的方法主要基于统计分析、神经网络和聚类分析，如支持向量机（SVM）、误差反向传播（Back Propagation，BP）算法、Bagging 算法等［11~15］。而对字符进行异常识别的方法相对较少，考虑到每个字符的维度是特别多的，而核零空间算法作为一种异常检测算法，并且考虑到它对于处理高维数据，以及提取数据非线性特征的优势，因此将其用于字符异常识别是合理的。

本文充分利用核零空间算法进行异常检测的优势，将其应用于字符异常识别，仿真实验结果表明，利用核零空间算法对字符进行异常识别，性能表现良好。

2 字符识别的发展

字符识别的发展是一个漫长的过程，20 世纪70 年代才由中科院自动化所的戴汝为院士牵头进行手写体字符识别，并在1974 年将所研究的手写体数字识别系统应用到邮政信件的自动分拣中。70 年代末开始进行汉字识别的研究，到1986 年汉字识别的研究进入一个实质性阶段，取得了较大的成果［16］。

传统的用来进行字符识别的方法大多还是集中于对字符识别进行分类，不同的字母对应一个不同的类别，因此常用来进行大量数据的整理、分类等领域。但若要检测字符数据集中的异常字符，核零空间算法则是一种合适的识别异常字符的方法。

3 核零空间算法的算法描述

核零空间算法是一种基于最大化Fisher 准则的一分类算法，Fisher 线性分类器由R.A.Fisher 在1936 年提出，之后在该分类器的基础上，Foley 和Sammon 基于最大化Fisher 准则提出了Foley-sammon 变换［17］，但之后，Foley 和Sammon 发现当样本数远远小于它的维数时，会出现类内散度矩阵奇异的情况，这时，会导致后续无法计算。基于该问题，许多研究者想到利用PCA 方法来进行降维来得到最终结果。之后，Chen 等［18］和Yu and Yang［19］基于最大化类间散度，最小化类内散度的原则，希望将类内散度矩阵利用某种变换将其投影为0，从而有效解决类内散度矩阵奇异的问题，因此提出了零变换，再结合FST 变换，得到NFST 变换。随后，在2008 年，Y.Lin，G.Gu，H.Liu，and J.Shen 又从数据本身出发，考虑到数据不仅具有线性特征而且具有非线性特征，因此基于数据的非线性，提出了核零空间变换，先将数据映射到高维空间中，再进行零空间变换［20］。此方法的应用，有效提取出了数据的非线性特征，并且表现良好。

3.1 Fisher准则

假设φ为LDA算法的投影矩阵，则

Fisher准则公式为

设总样本X={X1,X2,…,Xn}，N为总样本个数，n为总类别数，ni为第i类样本的个数，分别为第i类样本Xi的平均值，xij为第i类第j个样本，则分别可以将类内散度矩阵SW与类间散度矩阵Sb定义如下：

基于最大化Fisher准则，则上式可表示为

其中φ可表示为SbSW-1的前P 个最大特征值对应的特征向量所组成的投影矩阵，即φ={φ1,φ2,…,φp}，其中，φp为投影矩阵的第p个投影向量。

但是，在样本数远远小于样本的维数时，很容易造成Sw为奇异矩阵，这时很可能会导致投影向量无法求解的问题，即小样本问题。

3.2 NFST变换

为了解决上述小样本问题，我们引入了零空间变换，先提取Sw的零特征值对应的特征向量构成零空间，然后再在此基础上提取Sb的前p个最大特征值对应的特征向量。具体过程如下：

令：

引入了总散度矩阵St，令：

若存在零投影方向矩阵φ={φ1,φ2,…,φp}，使得 公 式φT SWφ=0成 立，则 此 时，φT Sbφ>0与φT Stφ>0等价。

令Zt和Zb分别为St和Sb的零空间，分别表示为

则非零向量矩阵φ属于Zt⊥∩Zw的子空间中，其中，Zt⊥和Zb⊥分别表示Zt和Zw的正交空间。

设θ1,θ2,…,θm为Zt⊥子空间的正交基，则在该子空间中的任一向量φ都可以表为

其中B为γ在正交基θ下的系数矩阵。

对于公式φT SWφ=0 ，其实际上与Swφ=0 等价，又由于φ∊Zt⊥∩Zw，则：

且此时BT(θT Swθ)B=0 与(θT Swθ)B=0 等价，因此我们便可以求得零方向投影矩阵φ。

3.3 KNFST变换

虽然利用NFST 变换成功解决了小样本问题，但是它却仅仅考虑了样本的线性特征，忽略了一些隐形的非线性特征，这很容易造成最终的结果不准确，因此就引入了后来的核零空间算法。具体描述如下：

设经过非线性映射后的特征空间为F，非线性映射后的样本为φ(X)，其中φ(X)={φ(X1),φ(X2),…,φ(Xn)}，n为类别数。

设在F空间中，ni为第i类样本的个数，φ(xij)为第i类第j个样本，为第i类样本φ(Xi)的均值，N为总的样本个数，则此时有：

第i类的类内均值：

总均值：

类内方差矩阵为

类间方差矩阵为

总方差矩阵Sφt为

由于进行了非线性映射以后才计算零投影方向矩阵的计算，因此需要对非线性映射后的核矩阵进行零投影方向的计算，其中核矩阵是由不同类不同样本间的内积构成的，即有：

核函数：

其中，i,k=1,2,…,n,j=1,2,…,ni,l=1,2,…,nk。

核函数矩阵为

核类内方差矩阵为

核类间方差矩阵为

核总方差矩阵为

则此时的条件为

非零向量矩阵φ位于Kt⊥∩Kw的子空间中。

设θ1,θ2,…,θm为Kt⊥子空间的正交基，则在该子空间中的任一向量φ都可以表示成：

对于公式φT KWφ=0，其实际上与Kwφ=0 等价，又由于φ∊Zt⊥∩Zw，则：

且此时BT(θT Kwθ)B=0 与(θT Kwθ)B=0 等价，因此我们便可以求得零方向投影矩阵φ。

本文中首次将核零空间算法用于UCI 数据集中的字符识别数据集，首先需要将所有的训练样本利用某个核函数进行非线性映射得到核矩阵，之后再计算核矩阵的零投影方向矩阵，将核矩阵按照该零投影方向，将整个训练集映射为零空间内的一个正常点，之后，将每个测试样本都通过该零投影方向进行映射得到零空间中的一个点，最后计算零空间中每个测试样本到正常点的距离，并且将此距离与事先设定的异常阈值进行对比，若超出该阈值则判断为异常样本。并且核零空间算法作为一种一分类算法，相较于其他分类算法，它仅需要使用正常类样本作为训练集，计算出零空间的投影即可，而其它分类算法则需要同时利用正常类与异常类样本一起作为训练集进行计算，这无疑会增加很多计算的工作量。并且通过与其他一分类算法的性能进行比较，可以发现，将该算法用于该字符识别数据集中，性能表现较好。

4 实验及分析

我们选取UCI 数据集中的字符识别数据集中的合成数据集［21］，该数据集是由不同形式的A-Z26个字符组成的，原来每个字符的维度为16 维，具体特征主要包括：图片的水平尺寸x-box、图片的垂直尺寸y-box、像素的宽度width、像素的高度high、像素的总数cnpix、图片水平尺寸的平均像素值x-bar、图片垂直尺寸的平均像素值y-bar、水平尺寸均方差x2bar、垂直尺寸均方差y2bar、水平均值与垂直均值的相关性xybar、x2y的均值x2ybr、xy2的均值xy2br、从左到右边缘计数的均值x-ege、x-ege 与y 的相关性、从底到顶的边缘计数的均值y-ege、y-ege 与x 的相关性。为了进行异常点检测，我们选取其中3 个字符，共有1600 个字符样本作为总的数据集，其中正常样本有1500 个，异常样本有100 个，并且为了验证算法在高维空间上的有效性，将其维度进行任意组合，例如可以将1，2 维组合，4，5，6 维组合等，这里我们将1，2 维；2，3 维；3，4 维；4，5 维；5，6 维；6，7 维；7，8 维；8，9 维；9，10维；10，11 维；11，12 维；12，13 维；13，14 维；14，15维；15，16 维；1，8 维进行组合，得到新增的16 个新特征，从而将整个数据集变成一个32维的数据集。

4.1 数据预处理

1）缺失值处理：经检测，该数据集没有缺失值。

2）数据归一化处理

线性函数归一化：将数据转换为［0，1］之间的数。

z-score 归一化：将数据转换为服从于均值为0，标准差为1的标准正态分布的数据。

3）核函数确定

考虑到字符数据的非线性特征，因此在利用核零空间算法对字符数据进行计算时，必须先选择合适的核函数，将数据进行非线性映射到高维空间中，再进行零变换，因此选择合适的核函数是必要的。常见的核函数有：线性核函数、多项式核函数、高斯核函数、幂指数核函数、拉普拉斯核函数等。

线性核函数：

多项式核函数：

高斯核函数：

幂指数核函数：

拉普拉斯核函数：

4.2 实验及结论

由于考虑到不同归一化处理以及不同核函数下的测试结果是不同的，因此，我们分别尝试对数据在不同的归一化处理下，选择不同的核函数进行ROC曲线测试的结果进行分析。

首先对数据进行线性函数归一化，令所有核函数里面的相关参数c=0 与σ=1，多项式核函数分别取d=2，d=10，d=50，d=100，然后得到不同核函数下的ROC曲线如图1~图2。

图1 线性归一化后不同核函数下ROC曲线图

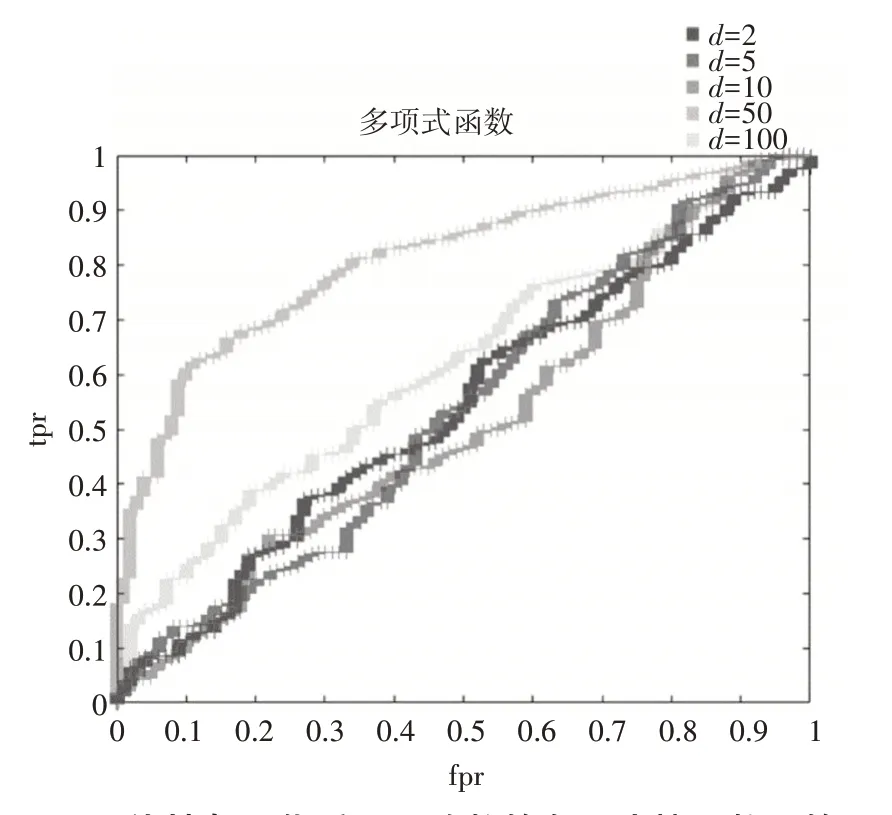
图2 线性归一化后不同阶数的多项式核函数下的ROC曲线图

通过观察图像我们可以发现，高斯核函数、幂指数与拉普拉斯核函数下的ROC 曲线呈现缓慢增长的趋势，并且在该数据集上表现良好，除此之外也可以通过调节它们的核参数得到其他不同的结果。但是线性核函数与低次多项式核函数则表现出近乎直线的增长趋势，并且性能表现较差。

仔细观察多项式核函数，尽管我们发现随着次数增长，图像越来越平滑，但是我们发现在d=50时，图像表现较为平滑，而在d=100 时，图像又呈现出直线的趋势，因此可以推测，在多项式核函数下，性能表现最优的d的取值位于［10，100］之间。

为了进一步更加直观地观察我们将核零空间算法用于字符异常识别的有效性，选择F1-score作为评测指标，得到不同异常阈值（均值与最佳值）下的结果，其中均值指的是所有测试样本到正常点的距离的平均值，最佳值指的是使得F1-score分数不等于1 时的最大值所对应的距离值，具体结果如下。

线性函数归一化不同核函数下的不同异常阈值的F1-score结果见表1。

表1 线性函数归一化不同核函数下的不同异常阈值的F1-score结果

观察表格我们发现，当取均值作为异常阈值检测时并不是一个很好的选择，因为它的F1-score普遍低于取最佳值作为异常阈值下的F1-score。但不管取均值作为异常阈值还是最佳值作为异常阈值，在高斯核函数下的F1-score分数都比其他核函数下的值要大，这说明在线性归一化处理下的数据集，采用高斯核函数映射，性能表现最佳，而线性核函数下的值则最小，性能最差。除此之外，我们还发现，在幂指数函数与拉普拉斯函数下的性能表现差距不大，只有作为均值作为异常阈值时，才拉开差距。而对于多项式核函数来说，在d的值较小时，F1-score 是不断增大的，但是当，d≥50 时，F1-score 变化不明显，仅仅有很小的增加，再结合ROC 曲线，我们可以知道，虽然在d=100 与d=50时的最佳值的F1-score相同，但是，通过观察图像，可以发现，d=100 没有d=50 时的性能表现好。因此，判断一个模型的好坏要结合准确率与图像进行综合分析。

之后，我们又得出了在z-score 归一化处理下的不同核函数的ROC曲线图如图3~图4，同样令所有核函数里面的γ=1 与σ=1，多项式核函数分别取d=2，d=10，d=50，d=100。

图3 z-score归一化后不同核函数下ROC曲线图

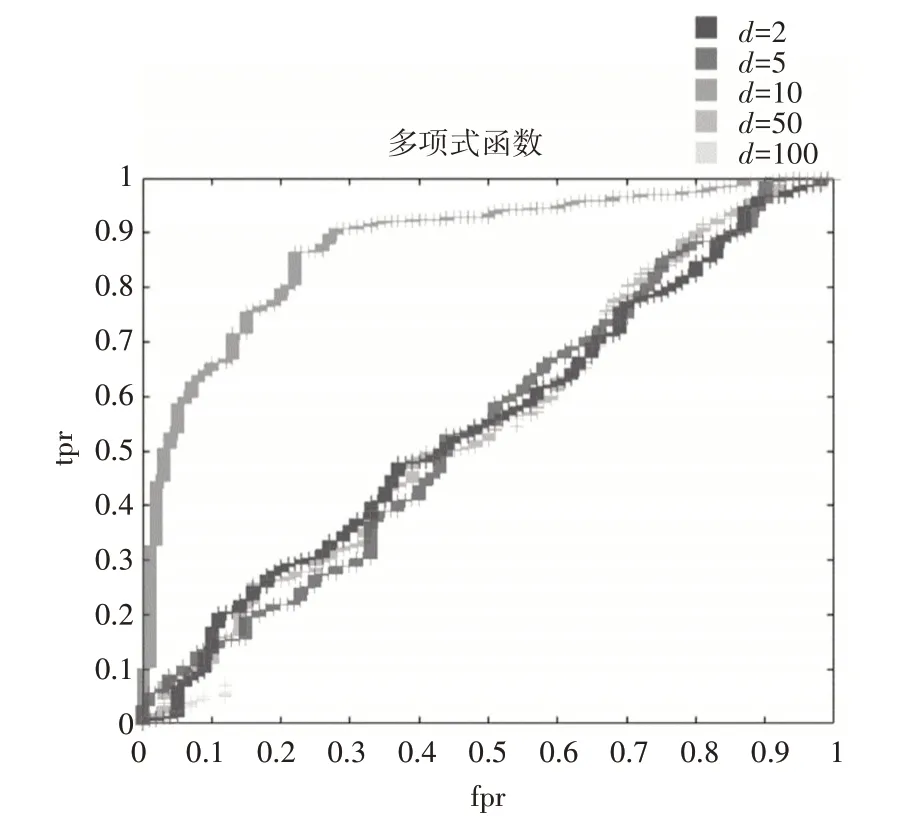
图4 z-score归一化后不同阶数的多项式核函数下的ROC曲线图

通过观察图像，我们发现被z-score 归一化处理后的数据集，在高斯核函数的映射下，在最初阶段F1-score出现了迅速增长，之后缓慢趋近于1，而在幂指数核函数与拉普拉斯核函数下，从一开始就是处于缓慢增长的态势，图像表现较为平滑。而线性核函数则使得ROC 曲线呈现出直线趋于1 的态势，这可能与线性函数本身的特点相关。而多项式函数在次数d为低次时，性能表现与线性核函数差不多，但是当d=10 时，图像也表现出与前面几种径向基核函数差不多的性能，但是随着次数的增加，当d=50 时，图像又近乎于直线趋于1，而在d=100 时，则出现了很多缺失值，实际上这是没有意义的，因为通过前面对d=2,5,10,50 下的考察我们已经发现，性能表现由坏变好之后趋于稳定，这说明，对于多项式核函数来说，在该数据集下，性能表现最好的d的取值，可能位于10左右。

z-score 函数归一化不同核函数下的不同异常阈值的F1-score结果见表2。

表2 z-score函数归一化不同核函数下的不同异常阈值的F1-score结果

观察表格，我们同样得出，经过z-score 归一化处理后的数据，在高斯核映射下利用最佳值作为异常阈值进行判别时得到的F1-score表现最佳，但是该映射下利用均值作为异常阈值时则表现最差，因此，在一个表现良好的核函数下，不一定任何异常阈值下的性能表现都是最好的。在幂指数核与拉普拉斯核函数下无论取均值作为异常阈值还是最佳值作为异常阈值，F1-score 分数都相同，再观察图像发现两者的性能表现几乎相同。而线性核函数在取均值作为异常阈值时，F1-score 分数是除了高斯核函数以外的最低，除此之外，它取最佳值作为异常阈值时，F1-score 分数与多项式核函数下的当d=100 时相同，取值最低。综合来看，线性核函数映射下的性能表现最差。在多项式核函数下，无论取均值作为异常阈值还是取最佳值作为异常阈值，性能表现在d≥10 后已趋于稳定，均值保持在0.9 附近，最佳值也稳定在0.9 附近，因此在实际应用中可以考虑选取d=10。

除此之外，为了更好地体现该算法的有效性，我们还将其他一分类算法用于该数据集，并与之进行性能比对，如表3。

表3 一分类算法性能比较

从表3 可以看出：对于one-class svm 算法、SVDD 算法与孤立森林算法，无论使用线性函数归一化还是z-score 归一化后的数据，它们三者的算法性能在两种情况下的表现都差不多，并且纵向对比之下，在one-class svm 算法上的表现相对来说较好，但是在SVDD 算法上的表现却极差，这可能与数据样本的分布不是球状有关。除此之外，这三种算法与核零空间算法相比，无论是使用线性函数归一化还是z-score 归一化，三种算法与之对应的最好的性能分别为one-class svm 算法的0.8636 与0.8643，但都位于0.9 以下，而核零空间算法在不同核函数下的最差的性能也分别为0.8989 与0.8989，接近0.9，因此，相比之下，核零空间算法在字符识别数据集中的表现更好。显然，将核零空间算法用于字符识别数据集是合理的。

因此，在利用核零空间算法进行异常检测时，对数据进行正确的归一化处理，并且选择一个合适的核函数以及选择一个不同核函数下的较为准确的异常阈值作为判断依据是值得我们仔细考量的。

5 结语

本文在当今时代对字符识别的处理大多集中在对数据集的整理与分类，很少用于异常识别的背景下，通过利用核零空间算法作为一种异常检测算法，在处理高维数据集，以及提取数据非线性特征上的优势，将其用于字符异常识别中，通过仿真实验表明，将核零空间算法用于字符识别是有效的。但考虑到，合适的异常阈值的选择往往特别依赖于数据集的选定，不同的数据集的最佳的异常阈值是不同的，因此在未来，如何在不限定数据集的情况下选择一个通用的异常阈值或者计算异常阈值的通用公式仍然是一个值得研究的课题。