平面向量考点探析

赵 妍

(黑龙江省大庆市第二十三中学)

在现行高中数学教材中,平面向量不仅仅以数学知识的“身份”出现,更是以解题方法的“角色”出现在各种问题的求解中.基于此,高考对向量的命题原则是“知识与方法并举”,那么高考命题中对平面向量的考查主要涉及哪些考点呢? 让我们一起来看看吧!

1 用向量证明垂直关系

向量是数与形的“结合体”.向量的“形”主要体现在它有方向.证明两条直线垂直就是证明两条直线所在的方向向量互相垂直,需要用到向量的数量积运算.由于平面向量在高考中一般以小题的形式出现,因此本考点常常以选择题的形式出现.

例1 (1)若O为△ABC所在平面内一点,且满足,则△ABC的形状为( ).

A.等腰直角三角形

B.直角三角形

C.等腰三角形

D.等边三角形

(2)若 平 面 四 边 形ABCD满 足,则该四边形一定是( ).

A.平行四边形 B.菱形

C.矩形 D.正方形

菱形,故选B.

这类问题主要考查平面向量的数量积运算法则,将题中所给出向量进行等价变形与运算,得到两个向量的数量积为0,从而判断它们有垂直关系.

2 用向量求夹角

A.0° B.30° C.60° D.90°

图1

图2

因为A是线段PE的中点,PE长为2a,所以

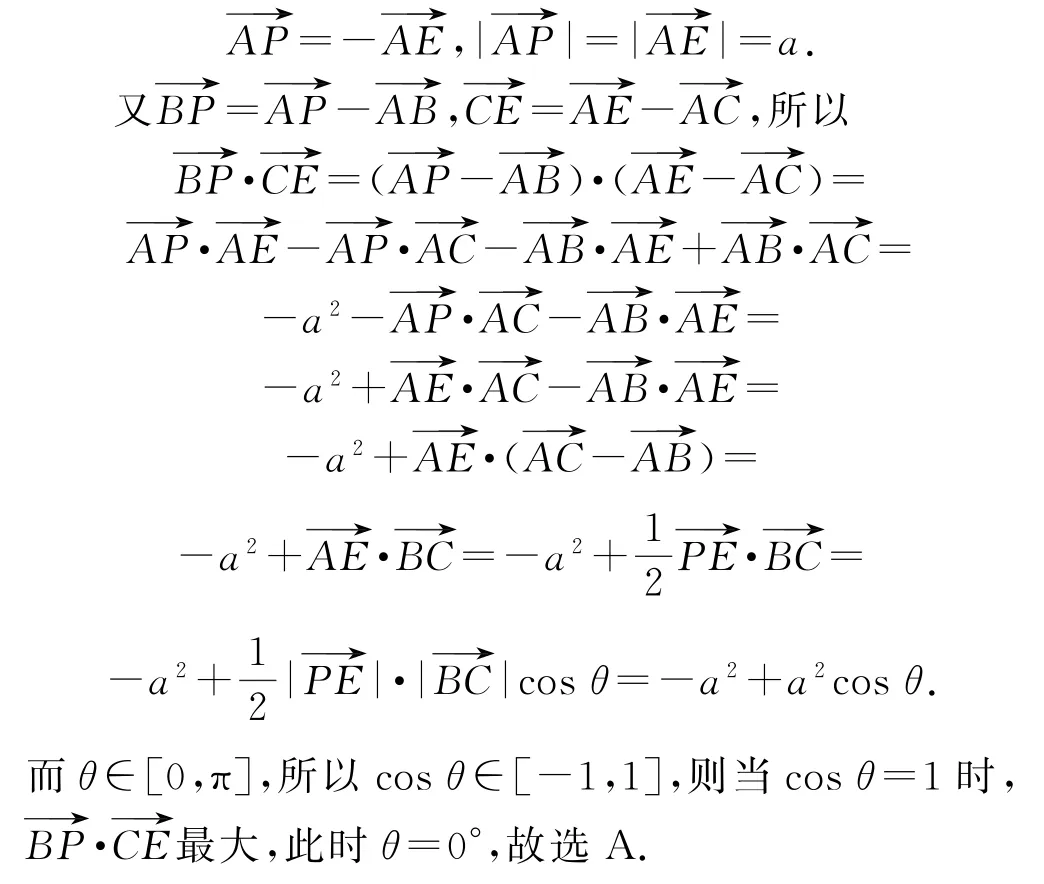
(2)以点A为坐标原点,AB,AD所在直线分别为x轴、y轴建立如图3 所示的平面直角坐标系.设BC＝3AB＝3,则点B(1,0),C(1,3),D(0,3),所以

图3

本例第(1)问采用的是基底转化法,其步骤是:1)选取基底;2)用基底表示相关向量;3)利用向量的线性运算或数量积找到相应关系;4)得出结果.本例第(2)问采用的是坐标运算法,其步骤是:1)建立适当的平面直角坐标系;2)把相关向量坐标化;3)通过向量的坐标运算找到相应关系.

3 用向量解决线段长度问题

求平面几何中的长度问题主要有两种方法:一是根据图形特点选择基底,对向量的数量积进行转化,再用公式|a|2＝a2求解;二是建立平面直角坐标系,确定相应向量的坐标,代入如下公式求解:若a＝(x,y),则

例3 已知E,F两点分别是四边形ABCD的边AD,BC的 中 点,且AB＝3,CD＝2,∠ABC＝45°,∠BCD＝75°,则线段EF的长为_________.

如图4所示,作AH//CD,交BC于点H,则∠BHA＝∠BCD＝75°,所以

图4

则

所以

本题的题干没有出现向量的有关信息,看似是一道纯粹的平面几何问题,但能应用平面向量法求解,体现了平面向量应用的广泛性.

高考对平面向量的考查以与几何问题结合为主,主要考查平面向量的基本运算和应用.因此,我们在复习平面向量相关内容时不仅要抓基础知识,更要掌握平面向量的综合应用.

(完)