例谈三角形中线长最小值问题的求解方法

胡厚松

(重庆市巫山县第二中学)

在知识点交会处设置问题,考查学生对多个知识点的灵活、综合运用能力,这是近年高考试题命制的一个突出特点.基于此,关注三角形中线长最小值问题的常用解法,有利于帮助我们厘清解题思维,提升相关数学知识点在解题中的灵活、综合运用能力,进而提升直观想象、数学运算以及逻辑推理等方面的核心素养.

解三角形是新课标高考数学必考知识,而且此类问题的考查经常与其他知识紧密联系起来,侧重考查学生灵活运用所学知识分析、解决问题的能力,同时能够较好地考查学生数形结合、运算求解以及逻辑推理等能力.本文以多解探究的形式对三角形中线长最小值问题进行剖析,旨在帮助同学们逐步提高处理此类问题的能力.

题目 已知等腰△ABC中,AB＝AC,且△ABC的面积为2,则边AC上的中线BD的最小值为____.

思路1 设出等腰△ABC的腰长和底边长,则利用余弦定理可得到BD2的表达式;另外,根据△ABC的面积为2,可得到腰长和底边长满足的关系式.据此综合分析,并灵活运用基本不等式即可顺利求解目标问题.

解法1 如图1 所示,作AE⊥BC于点E,设AB＝AC＝2m,BC＝n,则AD＝CD＝m,BE＝.

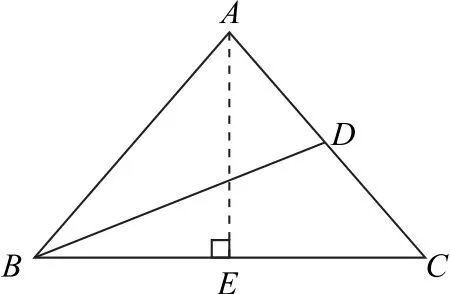
图1

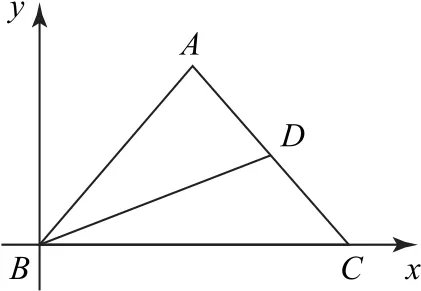
图2

在△ABD中,由 余 弦 定 理 得BD2＝5m2－4m2cosA.在△ABC中,由 余 弦 定 理 得cosA＝.于是,可得

解法2 同解法1作辅助线并设元,则在△ABD中,由余弦定理得

在△BCD中,由余弦定理得

又注意到∠ADB＋∠BDC＝180°,所以cos∠BDC＝－cos∠ADB,从而由①＋②可得4m2＋n2＝2m2＋2BD2,化简得.下同解法1.

1)解法1 灵活运用余弦定理的出发点是△ABD和△ABC具有公共角,而解法2灵活运用余弦定理的出发点是∠ADB和∠BDC的余弦值互为相反数.

2)借助基本不等式,巧求最小值的关键在于先消去“m2”,再活用基本不等式的变形结论“若a＞0,b＞0,则有,当且仅当a＝b时,等号成立”巧求最小值.

思路2 根据三角形第二面积公式可知△ABC的面积可与sinA紧密联系起来,而且根据余弦定理可知BD2可与cosA紧密联系起来,据此可考虑灵活运用正弦函数、余弦函数的有界性解题.

解法3 设AB＝AC＝2m,BC＝n,则AD＝m.因为△ABC的面积为2,所以,化简得msinA＝1.于是,在△ABD中,由余弦定理得

变形得BD2sinA＋4cosA＝5.易知存在角φ,使得

该解法的关键是先消去“m2”,再利用角A的正弦、余弦灵活表示BD2的表达式,然后借助辅助角公式以及正弦函数值的有界性构建不等式,最后通过化简不等式使问题获解.

思路3 由于本题涉及三角形的中线,所以可考虑三角形的中线向量公式,并对该式子两边取平方可得到BD2的表达式,然后借助余弦定理、基本不等式使问题顺利获解.

该解法与解法1和解法2类似,不同点在于先以平面向量的线性表示作为解题切入点,再灵活运用余弦定理和基本不等式求解,突出体现了对所学知识的综合运用能力.

思路4 由于本题涉及等腰三角形,显然图形具有一定的特殊性,又因为目标是求中线长的最小值,所以考虑采用坐标法求解.该解法适当建系并灵活设出点A的坐标,有利于结合图形特征迅速获得BD2的表达式,然后利用基本不等式即可巧妙使问题获解.

牛刀小试 已知△ABC的内角A,B,C所对的边分别为a,b,c,且满足

(a－c)(sinA＋sinC)－sinB•(a－b)＝0.

(1)求C;

本文分析了三角形中线长最小值问题的几种常用解题思路,有效沟通了解三角形、基本不等式、三角函数、平面向量、解析几何等知识的紧密联系,拓宽了学生的解题思维及视野,强化了学生对相关数学思想方法和知识的灵活、综合运用能力.

(完)