也谈正弦定理的证明与应用

魏 巍

(山东省济宁孔子高级中学)

数学处处呈现出和谐美,如解三角形经常用到的正弦定理:在△ABC中,若角A,B,C所对的边分别为a,b,c,则,三角形的三边长与三边所对角的正弦值成正比.那么这个定理究竟有哪些证法呢? 又有哪些应用呢?

1 正弦定理的证明方法

对于直角三角形来说,此定理显然成立,下面我们以△ABC是锐角三角形为例对该定理进行证明,当△ABC是钝角三角形时也可用这些方法证明,此处不再赘述.

1.1 转化为直角三角形问题

初中数学只研究解直角三角形,那么正弦定理的证明,能否转化为解直角三角形问题呢? 答案是肯定的,而且有两种方法.

证法1 作锐角三角形一边上的高,就可把原三角形变成两个直角三角形.

如图1所示,作CD⊥AB,垂足为D,则线段CD是边AB上的高,在Rt△CAD中,CD＝bsinA;在Rt△CBD中,CD＝asinB,则asinB＝bsinA,即

图1

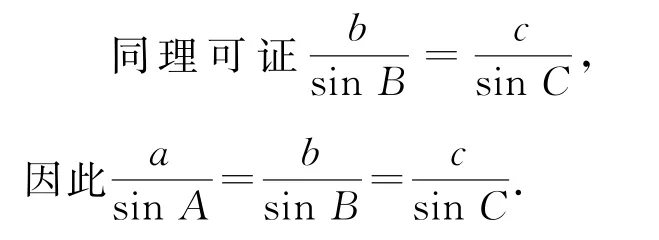
证法2 利用三角形的外接圆,同样可以把斜三角形转化为直角三角形.如图2所示,CD是锐角△ABC的外接圆直 径,连 接DB.设R为△ABC的外接圆半径,根据同弧所对的圆周角相等以及直径所对的圆周角是直角可得A＝D,∠DBC＝90°,CD＝2R,所以sinA＝

图2

1.2 利用三角形面积的三种表示

证法3 若△ABC为锐角三角形,则由证法1可知

这种证明方法简洁明了,体现了数学的简洁美.

1.3 利用坐标法

证法4 以C为原点、射线CA为x轴的正半轴建立如图3所示的平面直角坐标系,且使点B落在第一象限,则AC边上的高即为点B的纵坐标.根据三角函数的定义,知点B的纵坐标为h＝asinC,所以△ABC的面积为

图3

同理可得

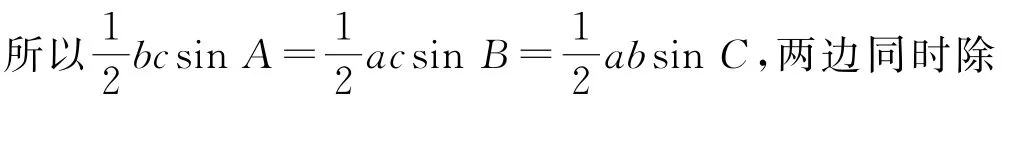
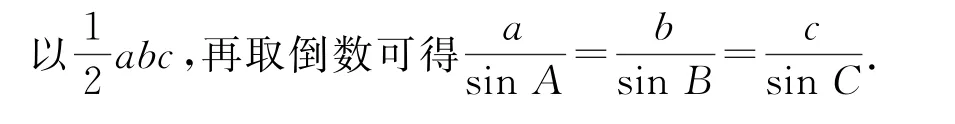
当然,正弦定理的证法还有很多,如教材上是利用平面向量的数量积来证明的,这里不再赘述.其实无论哪种证法,归根到底就是通过数形结合加以转化,转化成不同的知识和方法来证明.

2 正弦定理的应用

正弦定理体现了三角形中边与角之间的和谐关系,利用这个关系可以解决许多问题.

2.1 求解三角形中的最值问题

求解三角形中的最值问题的关键是写出所求量的三角函数表达式,而涉及边的问题往往需要利用正弦定理将边的问题转化为角的问题.

例1 如图4 所示,在Rt△ABC中,已 知∠A＝60°,∠C＝90°,AC＝4,则△ABC的内接正△DEF边长的最小值为_________.

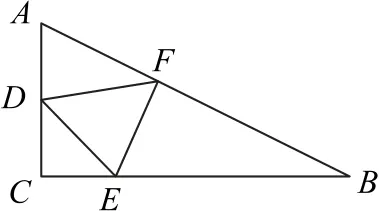
图4

因 为∠A＝60°,∠C＝90°,AC＝4,所 以BC＝ACtan60°＝,AB＝2AC＝8.

设正△DEF的 边 长 为a,∠DEC＝θ,在Rt△DEC中,DC＝asinθ,CE＝acosθ.因为∠DEF＝60°,所以

在△FEB中,由正弦定理得

所以

此题考查正弦定理以及三角函数恒等变换公式的应用,考查数形结合思想,解题的关键是在△FEB中借助正弦定理表示出BE,从而可表示出BC,再利用三角函数恒等变换公式化简变形可求出△DEF边长的最小值.

2.2 证明三角形中关于边的恒等式

对于三角形中关于边的恒等关系,往往可以用正弦定理转化为角的三角函数之间的关系,这是破解这类题的方向.

例2 在△ABC中,A为定角,且b＋c≤2a,求证:

证明 所证等式可变形为

在证明三角形中的边的关系式时,往往既要用到正弦定理又要用到余弦定理,有时还要用到三角恒等变换公式,本例中用到了二倍角公式、积化和差公式.

正弦定理能实现边与角的互化,在解答相关问题时,正弦定理可将目标式转化为统一角的关系式或边的关系式,从而为下一步解决问题创造条件.

(完)