探究“解三角形”章节的“教材题”

张 瑞

(山东省济南市章丘中学)

从历年高考试题中往往可以见到许多“教材题”的影子,所以我们有必要关注“教材题”.在研究“教材题”时,我们要注意与之相关的变式题,因为通过变式分析、研究有利于充分感悟、体验“教材题”的基础性和典型性.

1 根据三角形的三边长,求最大角

例1 (北师大版教材数学必修5第51页练习第2题)△ABC的三边之比为3∶5∶7,求这个三角形的最大角.

设角A,B,C所对的边分别为a,b,c,且a＝3k,b＝5k,c＝7k,其中常数k＞0,显然内角C最大.因为,而0°＜C＜180°,所以C＝120°,故△ABC的最大角为120°.

通过求解本题可知:如果一个三角形的三边长之比为3∶5∶7,那么这个三角形的最大角为120°,据此可设计相关的变式题.

变式1 已知A,B,C三地不在一条直线上,且A,B两地的距离为6km,B,C两地的距离为10km,A,C两地的距离为14 km,则△ABC的最大角为_______.

易知角B最大,由,从而可得B＝120°,故△ABC的最大角为120°.

变式2 (北师大版教材数学必修5 第56 页习题A 组第3题)如图1所示,在△ABC中,已知B＝45°,D是BC边上的一点,AD＝5,AC＝7,DC＝3,求AB的长.

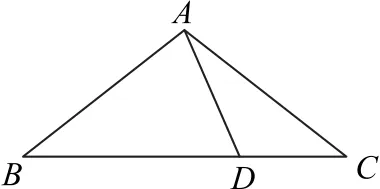
图1

在△ACD中,由余弦定理得

从 而 可 得∠ADC＝120°,∠ADB＝60°.于 是,在

2 根据三角形内角的关系,求三边长

例2 (北师大版教材数学必修5第57页习题B组第3题)在△ABC中,三边长为连续的正整数,且最大角是最小角的2倍,求此三角形的三边长.

通过求解本题可知:如果一个三角形的最大角是最小角的2倍,且三边长为连续的正整数,那么这个三角形的三边长分别为4,5,6.

变式 在△ABC中,角A,B,C所对的边分别为a,b,c,已知a＝4,b＝5,c＝6,求证:C＝2A.

证明 在△ABC中,由余弦定理得

又因为

所以cosC＝cos2A.

3 根据平面图形,求解圆内接四边形的面积

例3 (北师大版教材数学必修5第57页习题B组第2题)如图2所示,圆内接四边形ABCD的边长分别 为AB＝2,BC＝6,CD＝DA＝4,求 四 边 形ABCD的面积.

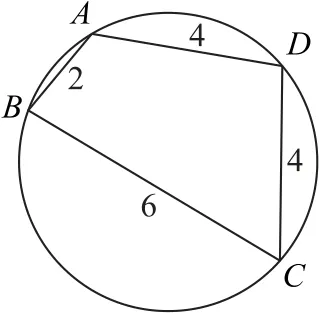
图2

连接BD,则在△ABD中,由余弦定理得

在△BCD中,由余弦定理得

通过本题的求解,我们应关注两点:一是求解不规则平面图形的面积可以考虑采用“分割与组合思想”;二是变换三角形,多次灵活运用余弦定理,可巧求角.

变式 某棚户区改造建筑用地平面示意图如图3 所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB＝AD＝4万米,BC＝6万米,CD＝2万米.

(1)请计算原棚户区建筑用地ABCD的面积及圆面半径R的值;

(2)因地理条件的限制,边界AD,DC不能变更,而边界AB,BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC上设计一点P,使得棚户区改造的新建筑用地APCD的面积最大,并求最大值.(1)连接AC,在△ABC与△ACD中,由余弦定理得

(2)设AP＝x,CP＝y,则由余弦定理得

又x2＋y2－xy≥2xy－xy＝xy,所以xy≤28.于是,有

当且仅当x＝y,即点P为圆弧ABC的中点时,等号成立,故当点P为圆弧ABC的中点时,棚户区改造的新建筑用地APCD的面积最大,最大值为平方万米.

关注对“教材题”的变式探究不但有利于巩固所学知识、方法,而且有利于深刻感悟“教材题”的基础性与典型性.

(完)