数学问题解答
2023年7月号问题解答
(解答由问题提供人给出)
2731在△ABC中,求证:
(陕西省咸阳师范学院教育科学学院 安振平 712000)
证明对△ABC的三内角A,B,C,由三角公式
sin(A+B)=sinAcosB+cosAsinB,
并应用柯西不等式,得
sin2(A+B)
=(sinAcosB+sinBcosA)2
≤(sin2A+sin2B)(cos2B+cos2A),

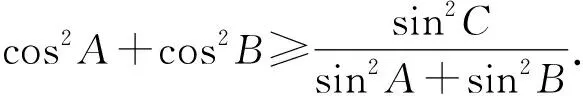
变形,得
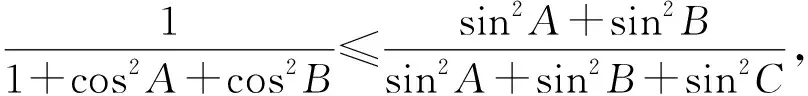

同理
将这三个不等式相加,便得


2732在△ABC中,角A,B,C的对边分别为a,b,c,AI,BI分别平分∠BAC,∠ABC,且∠ACB=60°,∠ABC=2∠BAC,求证:CI2=a2+c2-b2.

(山西省临县一中 李有贵 033200)
证明由∠ABC=2∠BAC得
因为a≠c,所以b2=a(a+c).
由∠ACB=60°得c2=a2+b2-ab.

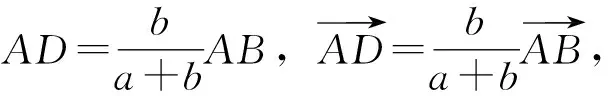

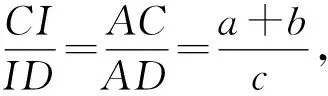
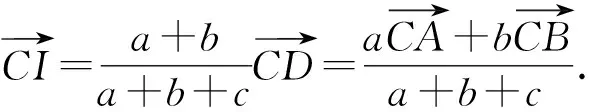

所以(a2+c2-b2)-CI2
=0,
即CI2=a2+c2-b2.
2733设a,b,c>0,且a+b+c=1,证明:
(1+a)(1+b)(1+c)
(广东省中山纪念中学 邓启龙 528454)
证明设x=a+b,y=b+c,z=c+a.
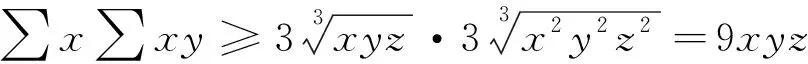
∑x∑xy=∏(x+y)+xyz

所以
∏(1+a)=∏[(a+b)+(a+c)]

(江苏省兴化市教师发展中心教研室 张俊 225700)
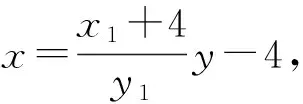
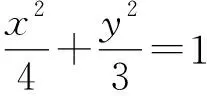
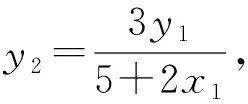
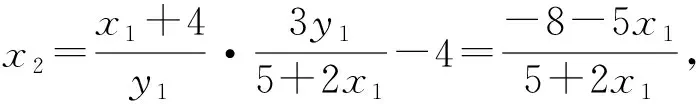
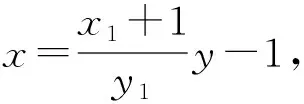
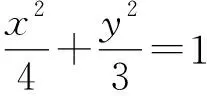
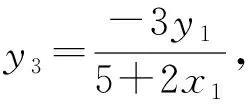

所以x2=x3,y2=-y3,
所以若C(x3,y3),则B(x3,-y3),
(x3-1)y4=-y3(x4-1),
即x3y4+x4y3=y3+y4,
=4y4-4y3,
则(x3-4)y4=(x4-4)y3,

所以直线CD过定点(4,0).
2735设△ABC的三条边,三个旁切圆半径,三条高线,面积和半周长分别为a,b,c,ra,rb,rc,ha,hb,hc,Δ,p,则
(天津港职工培训中心 黄兆麟 300456)
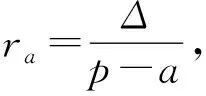

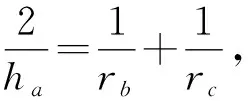
以上三个等式相加整理即得
由不等式(1)的完全对称性,
不妨设a≥b≥c,则有3a≥2p且3c≤2p,

那么此时设不等式(1)的左右之差为M,
则利用(2)就有
即不等式(1)成立.
2023年8月号问题
(来稿请注明出处——编者)
2736已知:如图,在△ABC中,∠ACB=90°,2AC=BC,点D1在CB的延长线上,点D2在BC的延长线上,BD1=CD2,过点C作垂直于AB的直线,垂足为M,与AD1交于点E1,与D2A的延长线交于点E2.求证:
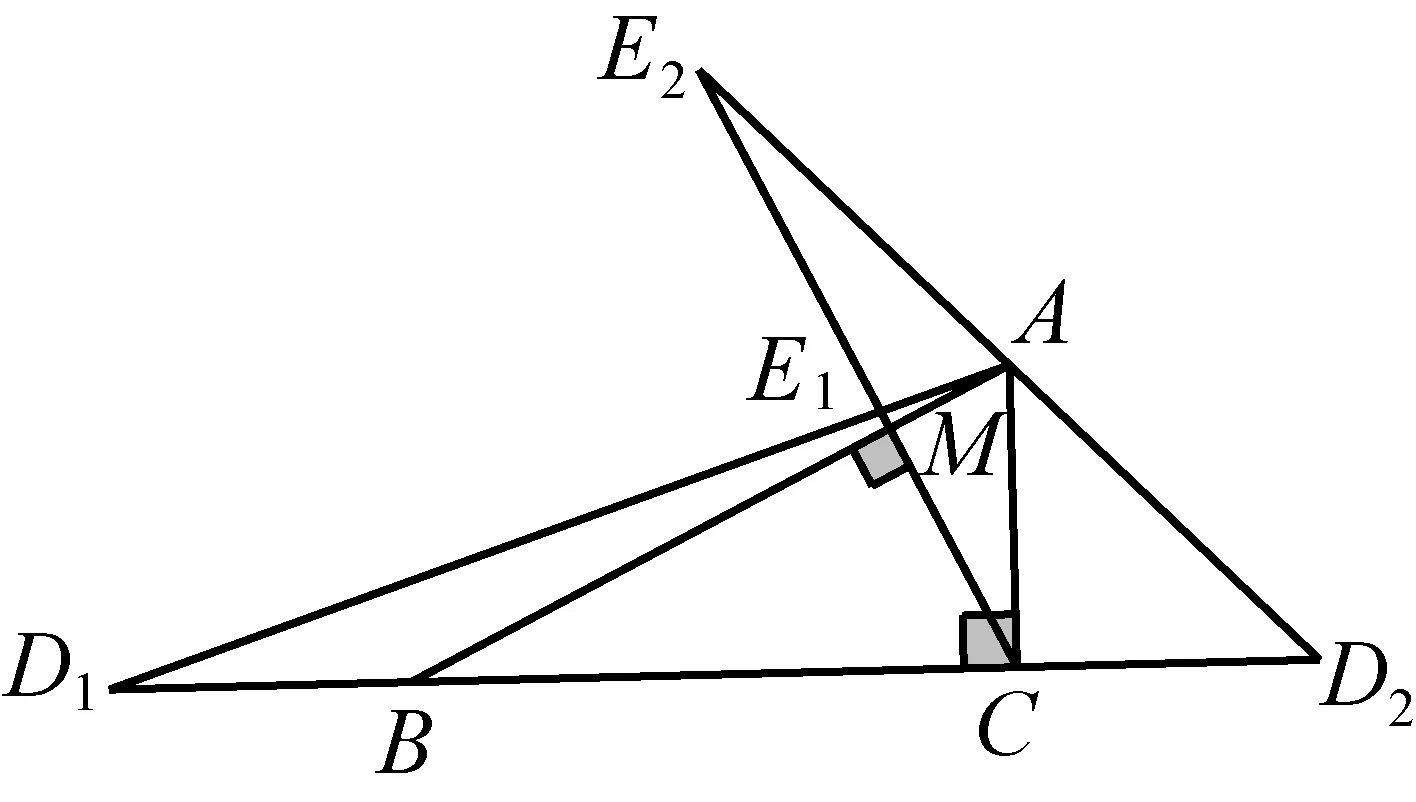
图
(北京师范大学附属实验中学 白玉娟 100032;北京市朝阳区郎各庄村21号 郭璋 100121)
2737设ai≥1,证明:
当且仅当n个ai中至少有n-1个为1时,等号成立.
(深圳市龙华区教育科学研究院附属外国语学校 钟文体 518109)


(湖北省南漳县建设工程质量监督站 刘光清 441500)
2739已知实数a,b,c满足a (安徽省南陵县城东实验学校 邹守文 242400) (浙江省慈溪实验中学 华漫天 315300)