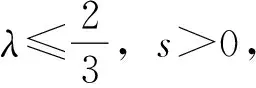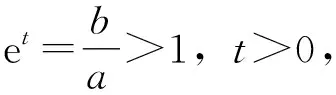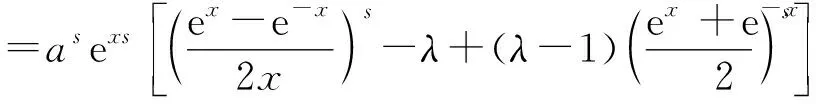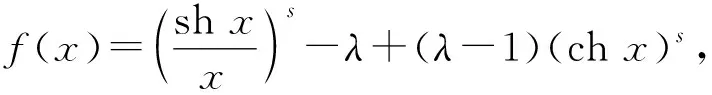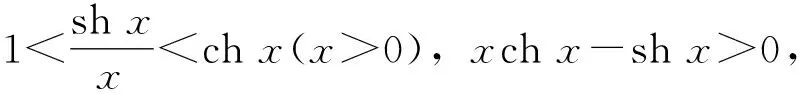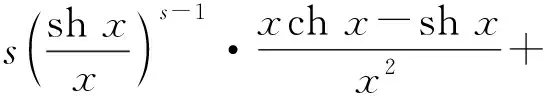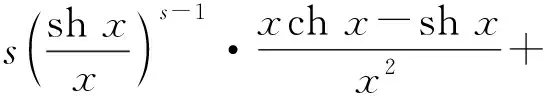关于对数平均的一个不等式的推广
李鸿昌 徐章韬
(1.北京师范大学贵阳附属中学 550081;2. 华中师范大学数学与统计学学院 430079)
1 引言
定义两个正数a和b的广义对数平均(Stolarsky平均)[1]为:
1975年,Stolarsky.K.B[2]证明了:当a≠b时,Lr(a,b)是r的严格递增函数.
经过计算,可得:
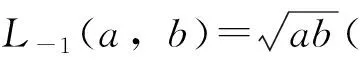
由Lr(a,b)的单调性和性质1,得到:
性质2当b>a>0时,Lr(a,b)有不等式链
L-∞(a,b)<… 即 则上式即 G (1) 1972年,B.C.Carlson[4]对G,L,A的关系进行了探究,得到 (2) 2001年,J.Sandor[5]对G,I,A的关系进行研究,得到 (3) 受(3)式的启示,姜卫东[6]研究了G,L,A之间的类似关系,得到 (4) 文[6]将(4)式进行推广,得到如下的一般结论. L2<λG2+(1-λ)A2. L2>λG2+(1-λ)A2. 笔者在研读文[6]时,发现定理1中λ的范围还可以修订,而定理2是错误的,应改为: 定理2′设λ≥1,则L2>λG2+(1-λ)A2. 笔者继续探索G,L,A之间的关系,然后将(2)、(4)式进行推广,且得到了更一般的结论. 证明由(1)式知 (5) 即 引理得证. 经过探索,笔者将(2)、(4)式进行推广,得到: 定理3设n>1,n∈N*,则 受到定理2′的启示,笔者继续探索,发现定理3中的指数n只要是大于0的实数都成立,于是将定理3推广得到: Ls<λGs+(1-λ)As. (2)设λ≥1,s>0,则Ls>λGs+(1-λ)As. 证明不妨设b>a,令t=lnb-lna, Ls-λGs-(1-λ)As s(λ-1)(chx)s-1·shx s(λ-1)(chx)s-1·shx 设 g(x)=xchx-shx+(λ-1)x2shx,x>0, 则 g′(x)=chx+xshx-chx+(λ-1)(2xshx+x2chx) =x[(2λ-1)shx+(λ-1)xchx]. 又λ-1<0,所以(λ-1)xchx<(λ-1)shx, 又shx>sh0=0,因此 g′(x) =(3λ-2)xshx≤0. 从而g(x)在(0,+∞)上单调递减,所以g(x) 显然,ch0=1. 由洛必达法则,知 所以f(x) 对于(2),当λ≥1时, 又shx>sh0=0,λ-1≥0,所以 s(λ-1)(chx)s-1·shx 从而f(x)在(0,+∞)上单调递增,所以f(x)>f(0)=0,故Ls>λGs+(1-λ)As. 评析经过恒等变形,把对数平均不等式问题巧妙地转化成了双曲函数不等式问题,形式简单、漂亮. 构造函数f(x),求导后利用引理进行放缩,再结合λ的范围,可得到f(x)的单调性,从而不等式得证. 定理的证明方法新颖,证明过程简洁、明了.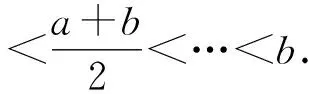
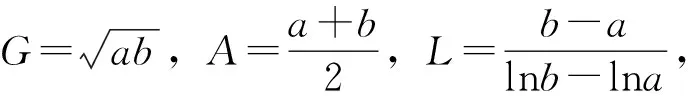
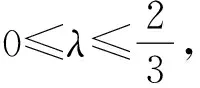
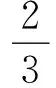
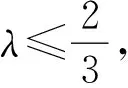
2 一个引理
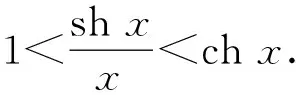
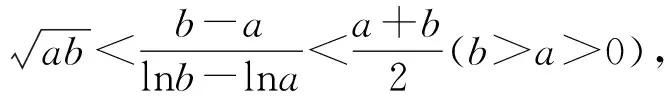
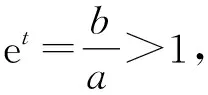
3 主要结果及证明