借助数学抽象 培养关键能力①——以“数轴上的动点问题”为例

潘竹树 李 祎

(1.福建省泉州市第九中学 362000；2.福建师范大学数学与统计学院 350108)

按照《义务教育数学课程标准(2022年版)》，抽象能力主要是指通过对现实世界中数量关系与空间形式的抽象，得到数学的研究对象，形成数学概念、性质、法则和方法的能力[1].史宁中教授指出：数学的眼光就是抽象，抽象包括数量与数量关系的抽象，图形与图形关系的抽象[2].本文以初一年级数轴上的动点问题为例，对照数学抽象能力分析水平框架，分析学生抽象能力培养方面存在问题及其原因，在此基础上结合实例分析如何提升学生的抽象水平，从而实现从会解一个题，到会解一类题，以培养学生的数学关键能力.

1 依据理论框架，开展教学诊断，挖掘抽象价值

1.1 数学抽象能力分析框架

数学抽象的表现是学生数学抽象能力测评的重要依据，数学抽象能力虽然不能被直接观测，但可以通过学生在具体任务中的实际表现加以推测.有关初中生数学抽象能力的测评依据与水平划分，尽管在《义务教育数学课程标准(2022年版)》中并未具体给出，但由于初高中的数学抽象具有本质的一致性和特征的相似性，因此我们可以参考和借鉴包括高中学段在内的现有研究成果，对初中生的数学抽象能力进行水平划分和测评研究.

数学抽象能力作为数学关键能力之一，涵盖数量关系与空间图形两个横向维度，可以划分为归纳与释义、关联与构建、拓展与普适三个纵向水平[3].据此，我们根据以下数学抽象能力分析框架，以作为判断初中生数学抽象能力水平的参考.

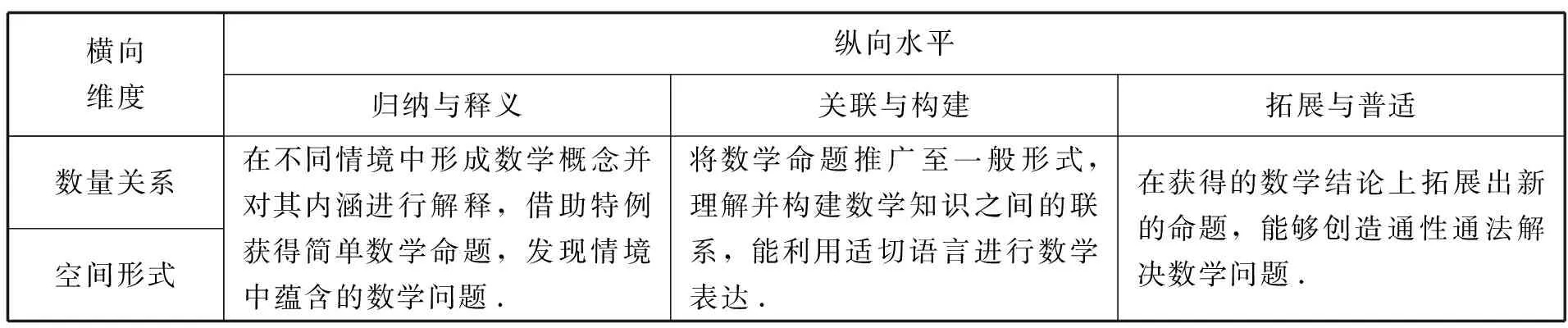
横向维度纵向水平归纳与释义关联与构建拓展与普适数量关系空间形式在不同情境中形成数学概念并对其内涵进行解释,借助特例获得简单数学命题,发现情境中蕴含的数学问题.将数学命题推广至一般形式,理解并构建数学知识之间的联系,能利用适切语言进行数学表达.在获得的数学结论上拓展出新的命题,能够创造通性通法解决数学问题.

1.2 一节同课异构课的教学诊断

日前，笔者在听初一的两节“同课异构”的数学课时，两位教师让学生做了如下同一道练习题.

如图1，数轴上点A、B分别表示-2和6，动点P以1个单位/秒的速度从点A出发向负半轴方向移动；同时，动点Q以2个单位/秒的速度从点B出发向负半轴方向运动.在A处有一个挡板，点Q碰到挡板后，立刻按原速返回.设点A运动时间为t，求当t取何值时，A、P两点间的距离与A、Q两点间的距离相等.

问题1归纳与释义方面，无法对P、Q两点间的距离及其内涵进行解释.

问题2关联与构建方面，无法用含参数的代数式表示动点P、Q的一般形式，无法构建“两点间的距离”与“数轴上的两动点间的距离”之间的联系.

问题3拓展与普适方面，无法从“一般数轴上点的移动”拓展到“变向”问题，无法创造通性通法解决实际问题.

1.3 数轴上动点问题的抽象价值

教学过程中，教师引导学生抽象起点过高、过程不充分和缺乏层次性，是导致学生抽象能力存在问题的主要原因.

数轴上动点问题的抽象，有两重抽象性：数量到数量关系的抽象，图形到图形关系的抽象.

抽象一：从“数”到“字母”的抽象，从“字母”到“单项式”的抽象，从“字母”到“多项式”的抽象.

抽象二：从“数”到“数轴上的点”的抽象，从“数轴上的点”到“点到原点的距离”的抽象，从“点到原点的距离”到“两点间距离”的抽象.

两重抽象之间还存在关联：“数轴上的点”可以用“字母”表示，“点与原点间的距离”可以用代数式表示，“两点间的距离”可以用代数式表示.

2 还原抽象原型，铺设抽象台阶，培养抽象能力

由于数轴上的动点的抽象具有复杂性、层次性和拓展性，在大单元教学理念的指导下，通过几个不同专题，还原数学抽象原型，细化抽象过程，从直观感知到理性思维，这是提升学生抽象水平的重要方式.

2.1 还原回到绝对值的意义，抽象两点间距离的本质

学生通过学习数轴，把小学阶段的“数”，抽象为初中阶段数轴上的“点”，实现从“数”到“形”的飞跃，数轴是培养学生抽象能力的良好载体.

出现问题1的主要原因，在于教学中教师认为数轴上“两点间的距离”很简单，“忽略”了知识的形成过程，没有让学生经历完整的知识形成过程，教学上的“跳跃”给学生造成抽象基础不稳固，而解决这个问题需要回到“绝对值的意义”这一概念.

如图2，我们把数轴上表示数a的点A与原点的距离叫做数a的绝对值，记作|a|.借助绝对值的定义，可理解AO=|a-0|，这里写成|a-0|，为学生理解两点间距离做铺垫.

图2

若数轴上表示数a的点A、数b的点B位于原点两侧、左侧和右侧，通过这三种不同情况的探究，让学生亲历抽象过程，得到A、B两点间的距离AB=|a-b|，当a≥b时，AB=a-b.

数轴上两点间的距离建立在绝对值意义的基础上，有利于学生从认知结构的“根部”建构所学知识，并通过分类讨论点A、B三种不同位置情况，形成对数量与数量关系的抽象、图形与图形关系的抽象.

2.2 还原回到动点从原点开始移动，抽象到动点从原点以外其它点开始移动

出现问题2，主要有以下两个方面原因：其一，移动的点不是从原点出发，给学生的抽象带来障碍；其二，学生抽象水平停留在“数”的阶段，不理解如何用含“字母”的代数式表示数轴上的点.

解决这个问题，需还原数轴上点的移动，从简单到复杂，逐步帮助学生抽象出如何用字母表示移动的点.

2.2.1 还原从原点出发的移动

学生经历知识生成的过程，积累从具体到抽象的基本活动经验，能够更好地理解知识的含义，提升数学抽象能力和抽象水平.

如图3，当从原点O出发的点向正半轴方向移动5个单位后到达点A，点A可以表示为0+5=5；同理，当从原点O出发的点向负半轴方向移动b个单位后到达点B，点B可以表示为0-b=-b.

图3

2.2.2 拓展到动点从原点以外其它点开始移动

如图4，点C表示1，如果点C向负半轴方向移动n个单位到点B，则点B表示为1-n；如果点C以2个单位/秒的速度向正半轴方向移动到点A，移动t秒后点A表示为1+2t.

图4

层次一：从原点开始运动，过渡到从原点以外其它点开始运动，起始位置产生变化；

层次二：用字母表示点C向负半轴方向移动到点B所表示的数，结合了运动的方向与距离；

层次三：除了结合运动方向外，还结合路程公式s=vt，抽象层次进一步提升，对学生的抽象能力要求更高.

2.3 还原到“临界点”为动点的出发点，抽象“反弹”类型的一般情况

出现问题3的主要原因，在于移动时遇到挡板“反弹”，学生无法用代数式表示“反弹”后的动点，“反弹”后动点的位置与运动的“方向”、“速度”、“时间”相关，对学生的抽象能力提出了更高层次的要求.

2.3.1 还原到动点从原点返回

如图5，动点Q从表示6的点B以2个单位/秒的速度向负半轴方向移动，在原点O处有一个挡板，当动点Q碰到挡板后立即按原速返回，则动点Q出发t(t>3)秒后在数轴上的位置怎么用含t的代数式表示？

图5

2.3.2 拓展到动点从原点以外的其它点返回

如图6，动点Q从数轴上表示6的点B以2个单位/秒的速度向负半轴方向移动，在表示-2的点A处有一个挡板，当动点Q碰到挡板后立即按原速返回，则动点Q出发t(t>4)秒后在数轴上的位置怎么用含t的代数式表示？

图6

3 变式拓展问题，提升抽象层次，培养抽象能力

学生的抽象水平在归纳与释义、关联与构建、拓展与普适等三个方面得到逐级提升之后，这样学生就可以轻松解决如上的“反弹”问题，在此基础上进一步拓展，在大单元教学理念的引领下，还可以进一步解决“变速”等问题.

3.1 提升抽象水平后，轻松解决“反弹”问题

当学生抽象水平提升后，学生能够轻松解决本文开头的问题.

当4≤t≤6时，因为AP=-2-(-2-t)=t，点Q表示为-2+2(t-4)=2t-10，AQ=2t-10-(-2)=2t-8，所以t=2t-8，t=8.

3.2 变式拓展问题，进一步提升抽象层次

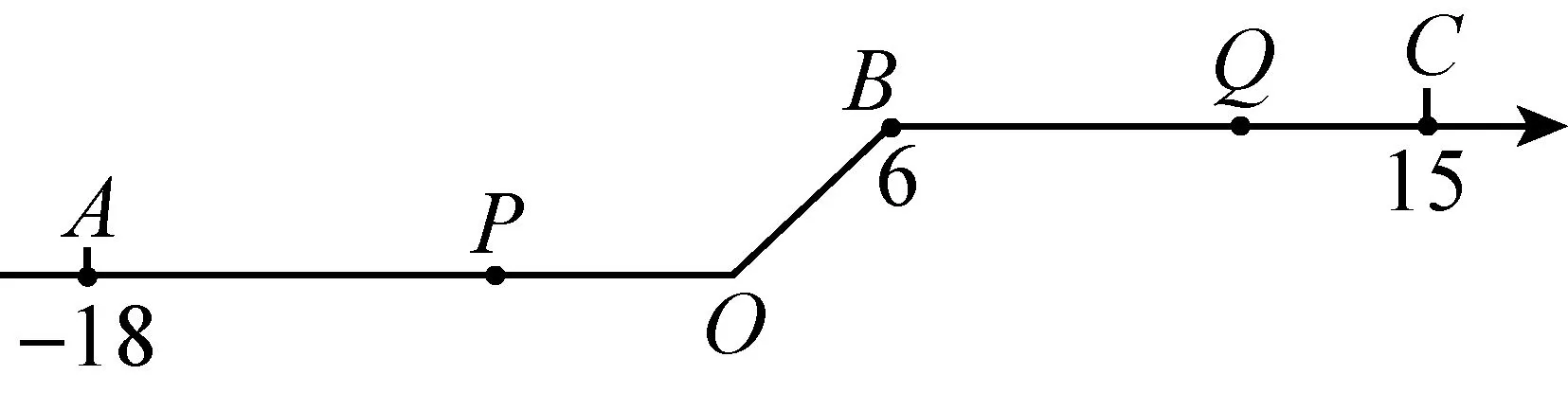
图7

假设在“折坡数轴”上，上坡时的移动速度变为水平路线上移动速度的一半，下坡时的移动速度变为水平路线上移动速度的2倍.动点P从点A处沿“折坡数轴”以2个单位/秒的速度向正半轴方向运动，运动到点O后，再上坡移动，当移动到点B时，立即掉头返回(掉头时间不计)；在点P出发的同时，动点Q从点C处沿“折坡数轴”以1个单位/秒的速度向负半轴方向运动，运动到点B后，再下坡移动到点O，然后再沿OA方向移动.当点P重新回到点A时所有运动结束，设点P运动时间为t，在移动过程中，

(1)点P在第几秒时回到点A；

解析：(1)18÷2+6÷1+6÷4+18÷2=25.5(秒).

(2)①当0

②当9≤t<12时，点P、Q都在线段OB上，点P表示为0+(t-9)=t-9，点Q表示为6-2(t-9)=24-2t，由t-9=24-2t，得t=11，此时P、Q相遇；

(i)当9≤t<11时，点P、Q都在线段OB上，且还未相遇，点P表示为t-9，点Q表示为24-2t，因为PQ=(24-2t)-(t-9)=33-3t，PO=t-9-0=t-9，所以33-3t=2(t-9)，t=10.2.

(ii)当11≤t<12时，点P、Q都在线段OB上，且已相遇，点P表示t-9，点Q表示24-2t，因为PQ=(t-9)-(24-2t)=3t-33，PO=t-9，所以3t-33=2(t-9)，t=15，不在11≤t<12范围内，不符合题意，应舍去.

③当12≤t<15时，点P尚未到达点B，点P、Q分别在线段OB、OA上，点P表示t-9，点Q表示0-(t-12)=12-t，因为PQ=(t-9)-(12-t)=2t-21，PO=t-9，所以2t-21=2(t-9)，方程无解，这种情况不成立.

④当15≤t<16.5时，点P从点B返回，点P、Q分别在线段OB、OA上，点P表示为6-4(t-15)=66-4t，点Q表示为12-t，因为PQ=(66-4t)-(12-t)=54-3t，PO=66-4t，所以54-3t=2(66-4t)，t=15.6.

⑤当16.5≤t<21时，点P、Q都在线段OA上，点P表示为0-2(t-16.5)=33-2t，点Q表示为12-t，因为PQ=(33-2t)-(12-t)=21-t，PO=0-(33-2t)=2t-33，所以21-t=2(2t-33)，t=17.4.

⑥当21≤t≤25.5时，点P、Q都在线段OA上，点P表示为0-2(t-16.5)=33-2t，点Q表示为12-t，因为PQ=(12-t)-(33-2t)=t-21，PO=0-(33-2t)=2t-33，所以t-21=2(2t-33)，t=15，不合题意舍去.

4 借助数学抽象培养关键能力的若干思考

4.1 回归抽象起点，重视抽象过程

数学抽象是相对的，高级抽象是在低级抽象基础上进行的[4].教学中，教师不能只关注复杂的抽象过程，而应回归简单的抽象，不应轻易跳过初步感知、建立模型、一般化和符号化的抽象过程，要夯实抽象的基础.在挑战难度较大的抽象问题时，回归抽象起点很有必要，好像一群在森林中迷路的人，回到出发点，有利于下一次重新确定行进方向，以摆脱困境.

数学教学应让学生经历完整的抽象过程、参与完整的抽象活动——感知与识别、分类与概括、想象与建构、定义与表征、系统化与结构化[5].在数学抽象的过程中，基本知识、基本技能相对容易获得，学生最欠缺、最需要的是基本思想的指导和基本活动经验的积累.在数学教学中，注重文字语言、图形语言与符号语言的转换，这是提高学生抽象水平的重要手段；注重引导学生仔细观察、直观感知、思辨确认，让学生更深入地理解抽象对象，这是提高学生抽象水平的关键；在抽象过程中加强学生间的交流，让学生在交流中取长补短，注重学生思维的碰撞，这样可以强化抽象能力的培养.

4.2 注重整体设计，提升抽象层次

《义务教育数学课程标准(2022年版)》在教学建议中指出：单元整体教学设计要整体分析数学内容本质和学生认知规律，合理整合教学内容，确定单元教学目标，并落实到教学活动各个环节，整体设计，分步实施[1].设计出体现数学的整体性、逻辑的连贯性、思想的一致性、方法的普适性、思维的系统性的系列化数学活动，引导学生通过对现实问题的数学抽象获得数学研究对象，构建研究数学对象的基本路径.

数学抽象活动的基本步骤为：分离属性与建构模型——概括与一般化——定义与符号化——系统化[6]．在有关数学抽象活动的教学中，教师同样要有大单元理念的指导，弄清知识的来龙去脉，理清本单元知识间的联系，厘清与其他章节的关系.教学中先布好局，对关键教学点进行必要的拓展，开展必要的项目式专题学习，有层次地串联知识，让学生拥有全局眼光、开阔视野，帮助学生建构系统知识体系，在循序渐进地逐级发展学生的抽象能力的同时，避免学生知识的碎片化，避免教学中出现亡羊补牢，以及头痛医头、脚痛医脚的现象.

4.3 重视抽象评价，优化抽象活动

《义务教育数学课程标准(2022年版)》在评价建议中指出，在关注“四基”“四能”达成的同时，要特别关注核心素养的相应表现.不仅要关注学生知识技能的掌握，还要关注学生对基本思想的把握、基本活动经验的积累，全面考核和评价学生核心素养的形成和发展[1].教学中，要细化每一项关键能力的评价指标，便于教师评估学生的学习表现，再根据学生的表现，调整教学，优化过程，更有针对性地培养学生的关键能力.

在有关数学抽象活动的教学中，课前教师要对相关教学内容进行分析，根据教学内容的抽象性进行教学设计，力求让学生制定策略，明确路径，经历完整的抽象过程；课中要对学生的抽象意识和抽象思维进行评估，做出及时调整，以更好地指导学生进行抽象活动，积累抽象活动经验；课后要根据学生的作业情况所反馈的信息做出评估，要制定并逐步完善评估标准，通过考试等手段长期跟踪学生的抽象能力发展水平，分析、比较与评估学生的数学抽象能力，根据学生学情并在理论指导下开展数学抽象活动.

4.4 研究抽象本体，关注人的发展

课程目标以学生发展为本，以核心素养为导向，进一步强调使学生获得“四基”，发展“四能”，形成正确的情感、态度和价值观[1].数学抽象素养是数学核心素养的重要组成部分，它不仅能帮助人们运用所学知识技能从具体情境中抽象出一般规律和结构，用数学符号、术语予以表征，而且数学抽象还是满足个体自身发展需要的必备能力及思维品质[7].

数学抽象是人必备的能力，通过抽象，进一步认识事物的特征，揭示事物的本质，把握事物之间的联系.数学抽象是学习的需要，在学习中通过抽象的过程，学习基本知识、基本技能，感悟基本思想，积累基本活动经验，深刻理解数学概念、命题以及知识结构与体系.数学抽象能够培养人的思维，教会人们抽取对象的数量关系和图形特征，辨析异同点，甄别有效信息，剔除干扰因素，抽象得到对象的本质属性，达到知行与思维的统一.

数学抽象能力的培养不是一朝一夕就能实现的，需要教师长期关注抽象素材，教学中细化抽象过程，实践中指导抽象方法，活动中积累抽象经验.抽象能力是学好数学最基本的能力之一，也是培养学生数学关键能力的重要抓手，需要教师从初一起始年级就开始渗透抽象思想，让学生感悟抽象过程，掌握抽象方法.