学科德育视角下的“祖暅原理”设计与教学实践①

沈金兴

(浙江省桐乡市凤鸣高级中学 314500)

1 高中数学学科德育

《普通高中数学课程标准(2017年版2020年修订)》(下简称新课标)的基本理念是“学生发展为本，立德树人，提升素养”，并明确将“数学教育承载着落实立德树人根本任务、发展素质教育的功能”作为数学课程的性质之一，因此数学也需发挥其学科德育功效.

数学学科德育就是指数学教师在数学教学中进行德育渗透，实现数学学科的育人价值[1].要在数学课堂上渗透学科德育，需挖掘教材中所蕴藏着的育人素材，而行之有效的途径之一就是融入数学文化，并以数学史为载体，潜移默化地发挥数学学科的德育功能.

人教社2019年出版的《普通高中教科书数学A版》(下简称新教材)是根据新课标理念编写的，其中有些栏目增添了许多值得挖掘的育人素材，比如选学内容中的“阅读与思考”“探究与发现”“文献阅读与数学写作”等.鉴于此，笔者对人教A版必修第二册选学内容“探究与发现”中的“祖暅原理与柱体、锥体的体积”进行了一次课堂实践，充分挖掘了教材中的育人元素，并将数学学科德育要素润物细无声地融入其中.

2 教学设计与实践

2.1 教学定位

学情分析：新教材中的选学内容“祖暅原理与柱体、锥体的体积”，安排在8.3节“简单几何体的表面积与体积”之后的“探究与发现”栏目中，此时学生的认知基础就是柱、锥、台、球的体积公式，脑中还没有形成理论体系，故立体感差，空间想象力弱是学生学习的逻辑起点.

教学内容分析：“祖暅原理”作为原理通俗易懂，在1990年版的人教社教材是作为公理来处理的，故只需说明原理正确即可.那么这个原理是在什么情况下发现的？怎么发现的？该原理发现后有什么用？等等，这些应该是本节课所要解决的问题.

查阅文献[2]，发现该原理正好能完整地呈现中国古代数学家的研究工作，体现了我国古代数学的辉煌成就，其中还蕴涵着很多育人素材，是一次给学生增加文化自信，提升民族自豪感的极佳机会.因此笔者将教学内容定位为：以探究祖暅原理为契机，来一次重走中国古代数学家的发现之旅，寓德育于课堂，进行一场爱国主义教育，从而实现从数学到文化、从文化到育人的教学目标.

2.2 教学过程

2.2.1 承上启下，提升思维

师：同学们，到目前为止，我们已知道了哪些体积公式？

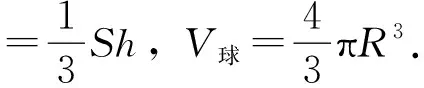
师：知道这些体积公式是怎么得来的吗？

生1：不清楚，记得读小学时，好像数学老师往容器里倒水后做实验得出的.

生2：初中数学老师好像是通过剪拼图形得来的.

师：很好，大家还有点印象，但这些都是直观感知.其实，我们前面学的体积公式也是直接告知的，你们觉得这样严谨吗？是否还应该再做点什么？

生(齐答)：应该要用理论进行推导.

师：说得好.高中阶段应该要进行理性思考，以提升思维能力.今天我们上一节选学内容中“探究与发现”的课：“祖暅原理”，来一次重走古代数学家的发现之旅.

设计意图高中生再学体积公式，应该从小学、初中时的直观认知上升到具有理论高度的思辨认证，这是一次思维层面质的飞跃，从而启发学生思考.所以，这样的设计既承上启下，又能激发学生的探究欲.

2.2.2 阿基米德的缺憾

师：图1是古希腊数学家阿基米德墓碑上的图案：圆柱容球.图上的3∶2是什么意思呢？

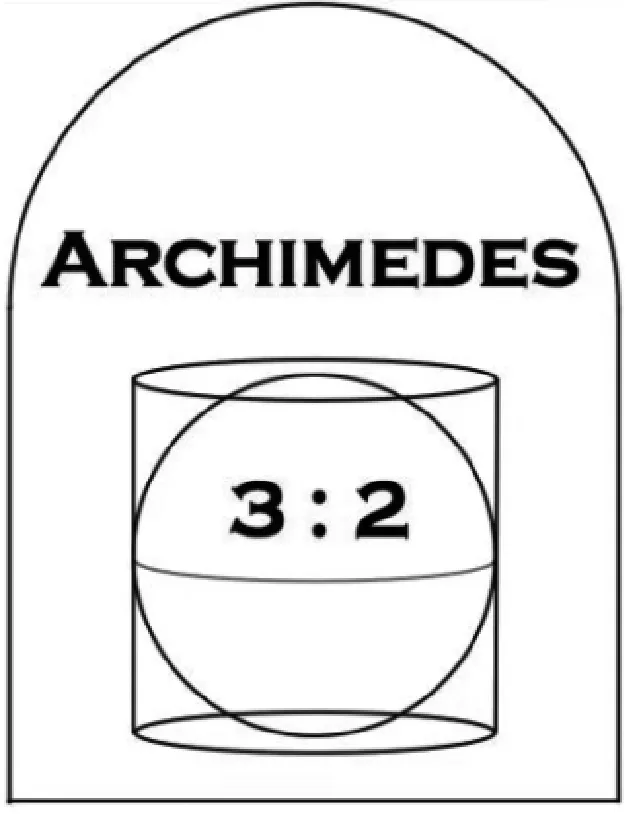
图1

生3：应该是指圆柱与球的体积之比是3∶2.

生4：圆柱与球的表面积之比也是3∶2.

师：都没错，阿基米德已经知道了圆柱、球等的体积与表面积公式，因此他引以为豪，将此作为了自己墓碑的图案.大家想想，一个该有多么热爱数学的人才会用数学图案来代替他的墓志铭啊！不过比较遗憾的是，阿基米德采用了物理中的力学方法来推导，而非纯几何的方法.在这方面，中国古代数学家作出了巨大贡献，他们前赴后继地研究球的体积公式，特别是在此过程中发现了更一般化的理论：祖暅原理.

设计意图从国外古代数学家阿基米德墓碑说起，既有趣味性又突出了数学家的痴迷，同时又开宗明义地引出了我国古代数学家的成就.

2.2.3 刘徽的遗憾

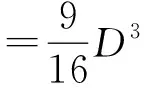
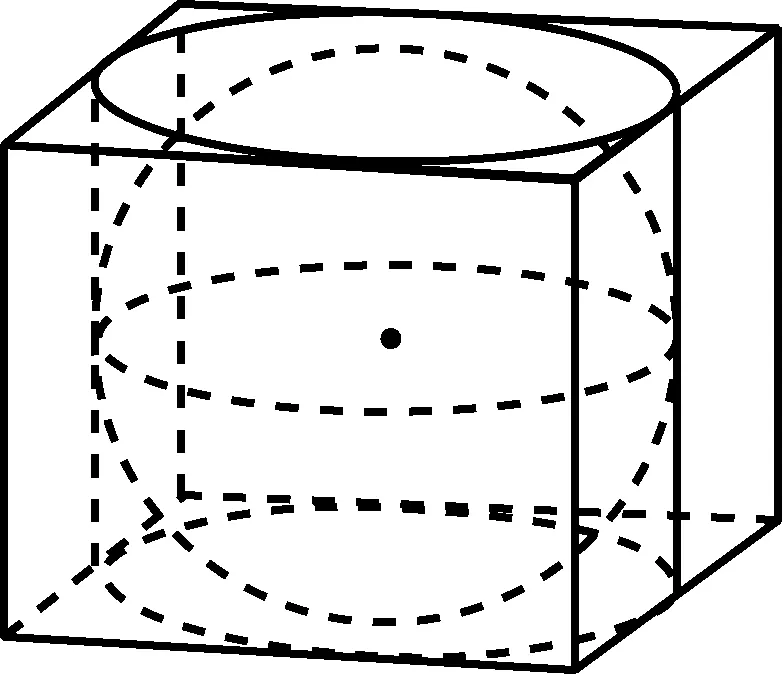
图2

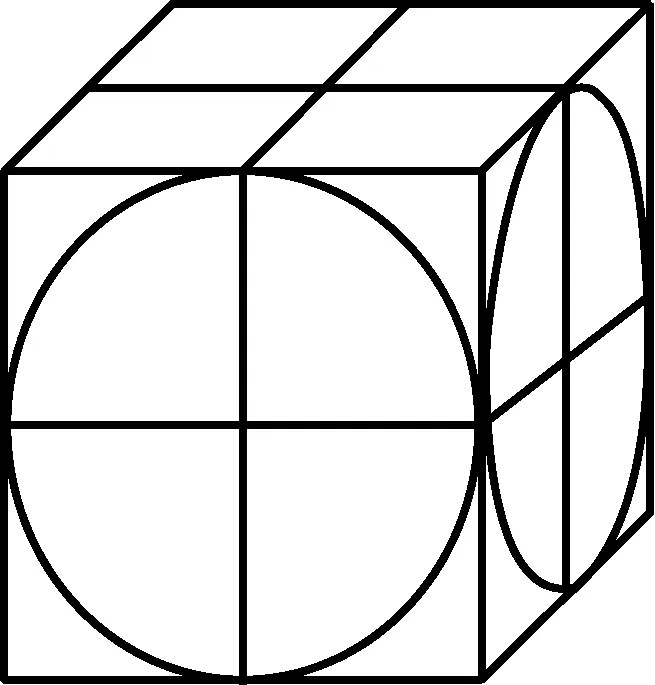
图3

生5：有点像两个水管的相交部分.

师：这位同学很有想象力嘛.为了能直观感受，见图片与视频(展示图4，图5，并播放用3D打印牟合方盖时的设计视频).

图5

师：请同学们观看实物(每组有2个牟合方盖让学生互相传递看，教师展示大的实物)，上下像两把对合的方伞，“牟”指相等的意思，故刘徽称之为“牟合方盖”(下简称合盖).其实，合盖内还有一个内切球，如图6.如果取图5的八分之一，并用平行于底面的截面去截，会得到什么图形？

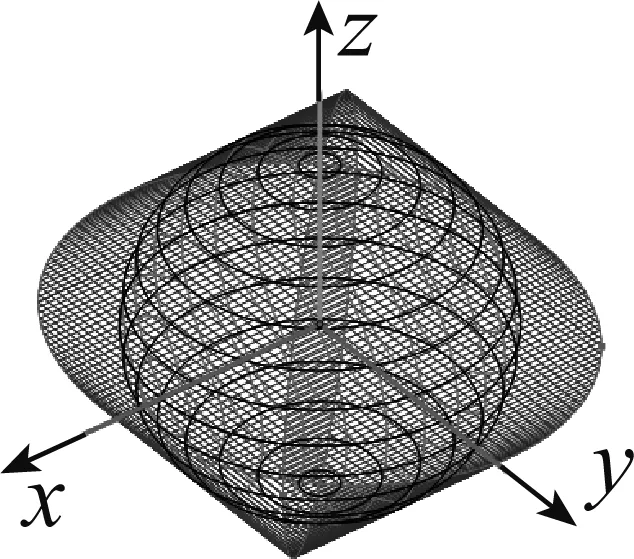
图6

生6：截面应该是一个正方形和四分之一圆.

师：是的，如图7.刘徽用了截面原理：如果两个等高的立体，用平行于底面的平面截得的截面积之比是定值，则这两个立体的体积之比也等于该定值.请同学们计算一下球与合盖体积之比.

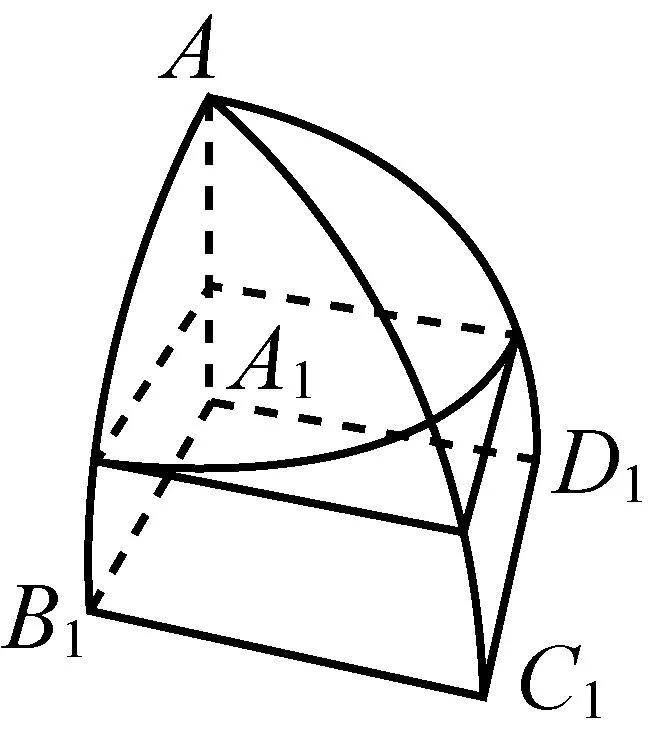
图7

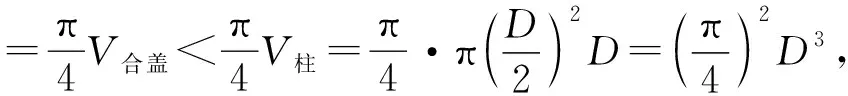
生8：有道理，但合盖的体积怎么求呢？

师：是的，刘徽也遇到了同样的难题.因为他被正方体内、合盖之外的太复杂的立体图形给难住了.于是留下了一句话：“敢不阙疑，以俟能言者”，意思就是我解决不了这个疑难问题，只能留着，希望以后更有能力的人解决它.这表明了刘徽敢于承认自己的不足，谦虚谨慎的高尚治学态度，并寄托于后辈学者的宽广胸怀.

设计意图通过详细呈现刘徽在推导球体积公式过程中所做的研究工作，让学生了解到中国古代数学家的创造力与实事求是、一丝不苟的严谨态度.

2.2.4 祖冲之的期望

师：200多年后，祖冲之诞生了.他继承了刘徽的研究工作，沿着刘徽思路继续求合盖体积.祖冲之把图3的八分之一拿出来，如图8，并称A-A1B1C1D1为“内棋”(图7)，然后将剩下的部分称为“外棋”.如果能算出“外棋”体积，那么合盖体积就能求出.

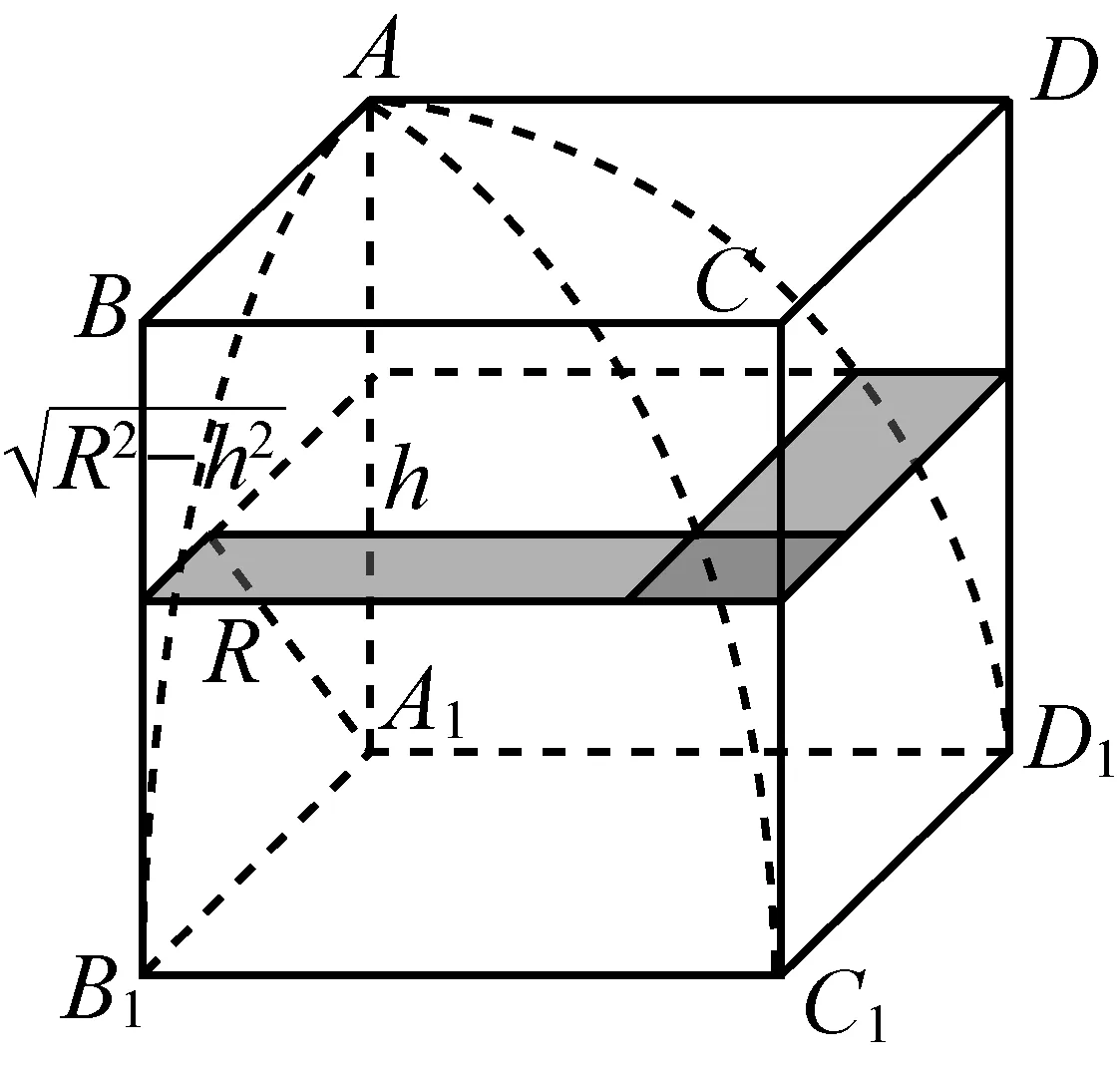
图8

生9：的确如此，可是“外棋”的体积也很难求呀！

师：是的，所以祖冲之又把“外棋”分成了三个部分，如图9.可惜到了这一步，祖冲之也遇到了困难，做不下去了.但他希望自己的儿子祖暅能子承父业，完成他的未竟事业.

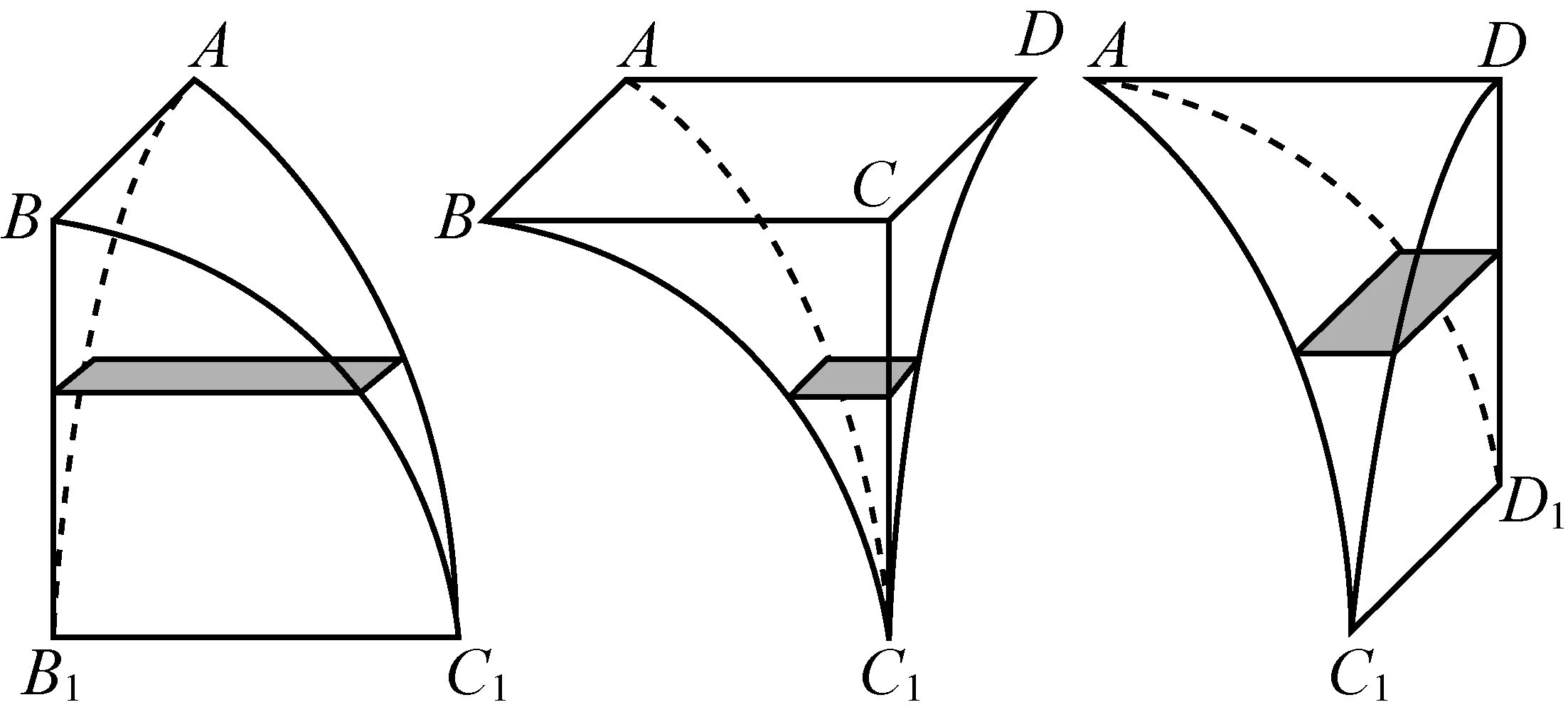
图9

设计意图祖冲之继承了刘徽的研究工作，虽未最终解决，但他把“外棋”分成3部分，为后续研究迈出了一大步，并期望儿子祖暅能有所突破.由此让学生明白，在科学研究的道路上，从来没有捷径可言，都是通过代代相传，历经千辛万苦才有可能成功的道理.

2.2.5 祖暅的突破

师：祖暅沿着父亲祖冲之的足迹继续研究.他想，刘徽与他父亲之所以研究不下去是由于“内棋”或“外棋”都不太好算，那能否进行转化呢？即将它们的体积化为比较好算的几何体的体积呢？于是祖暅联想到了刘徽曾经采用的截面原理.同学们，你能把该原理中的比值进行特殊化吗？

生10：当然是比值为1时最特殊了.

师：不错，根据截面原理，如果比值为1，那么两个几何体的体积就相等了.为此，祖暅做了大量的实验.现在我们不妨也来做两个实验.(教师分别演示了一摞书，见图10；倾斜容器里的水，见图11)

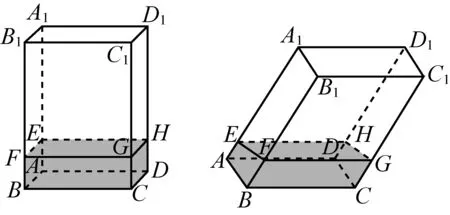
图11

生11：这不是很明显的嘛，实验前后的体积是不变的.

师：是的，结论显然成立，道理也浅显易懂，祖暅将它概括为：“幂势既同，则积不容异”，这就是“祖暅原理”.用现代语言描述：夹在两个平行平面之间的两个几何体，被平行于两平面的任意平面所截，若截得的两个截面面积总相等，则这两个几何体的体积相等.祖暅提出的这个原理，比西方数学家早了一千多年，欧洲直到17世纪才有数学家提出相同结论.

生12(很惊讶)：我国古代数学家这么厉害，崇拜了！

师：的确，我国古代的数学成就很高的.下面看看祖暅是如何解决球的体积问题.

先看图3，设球半径为R，则外切正方体棱长为2R，其八分之一小正方体棱长也是R.再看图8，在离底面A1B1C1D1任意高h处作平行于底面的平面，截内棋为1个正方形.显然，这个正方形面积为R2-h2；与此同时，截外棋得2个长方形和1个小正方形，即图8中的阴影部分，其面积和为：R2-(R2-h2)=h2，也就是图9中3个阴影部分面积和.因此，祖暅构造了一个底面边长与高均为R的倒立阳马(古人将底面为正方形，有一棱垂直于底面的四棱锥称为阳马)，如图12，再在距顶点C1为h处作一截面，显然截面面积为h2，正好等于外棋在同一高处的截面积，根据祖暅原理有：V外棋=V阳马.

图12

师：很好，有了祖暅原理，就解决了祖冲之面对外棋没法做下去的难题.由此可见，祖暅原理是在推导球体积公式的过程中发现的，但它前后却经历了200多年，从刘徽到祖冲之再到祖暅，正是一代代数学家坚持不懈地薪火相传才终获成功.

设计意图祖暅原理的发现并非一帆风顺，它是三代数学家面对困难永不放弃，坚持到底才有所获.课堂上重走这样的一次发现之旅，不仅让学生体会到中国古代数学的杰出成就，增强了民族自豪感，而且还可让学生懂得任何知识都来之不易，如今的我们也要继承这种刻苦钻研精神.

2.2.6 祖暅原理的应用

师：知道了我国古代数学家推导球体积公式的经历后还要明白，比球体积公式更重要的是发现了祖暅原理.因为有了该原理，可将几何体进行转化.如柱体积公式的推导，图13.

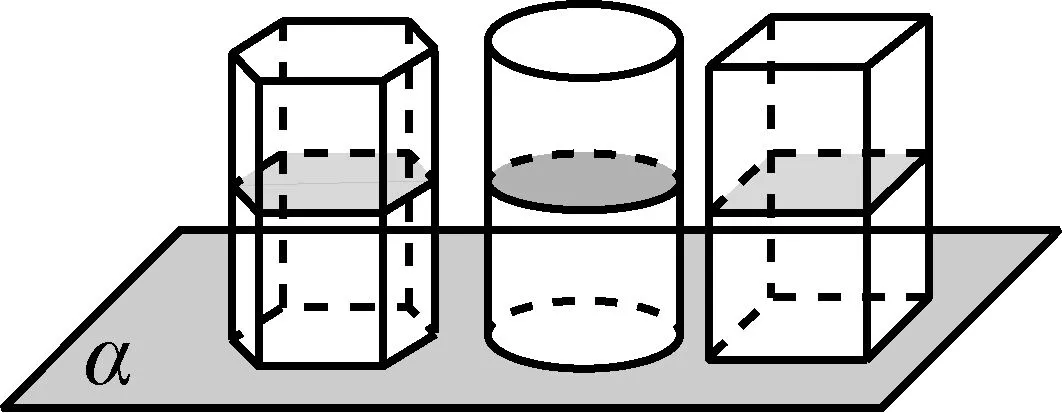
图13

生14：因为截面处处相等，所以V棱柱=V圆柱=V长方体=S底h，即V柱=Sh.

师：很好，再看图14，15，又可得出什么？

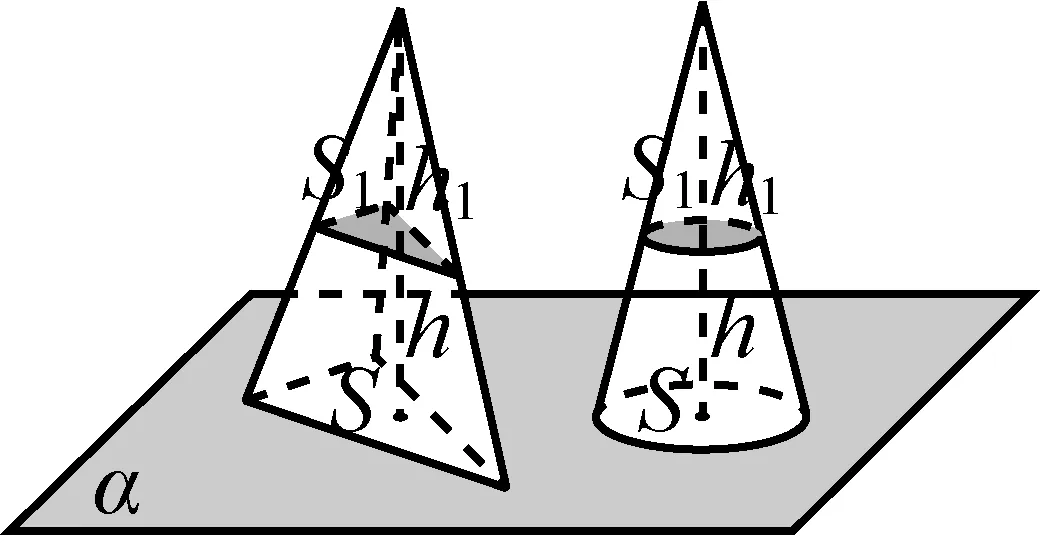
图14

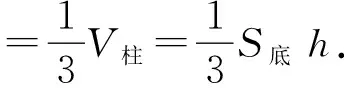
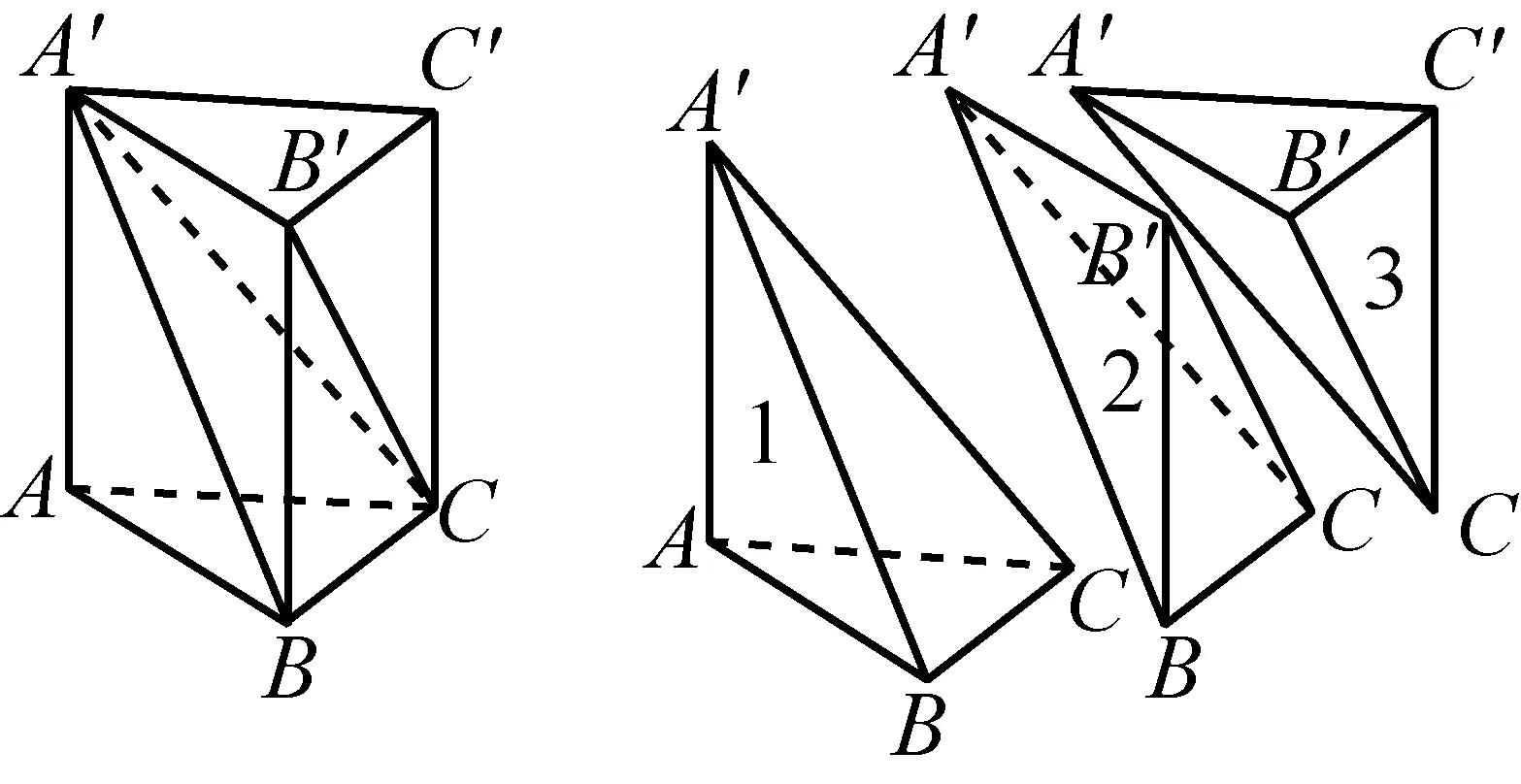
图15

师：非常好，有了祖暅原理，柱体、锥体的体积公式很容易得到.事实上，应用该原理还可反过来很方便地推导球体积公式，见图16.

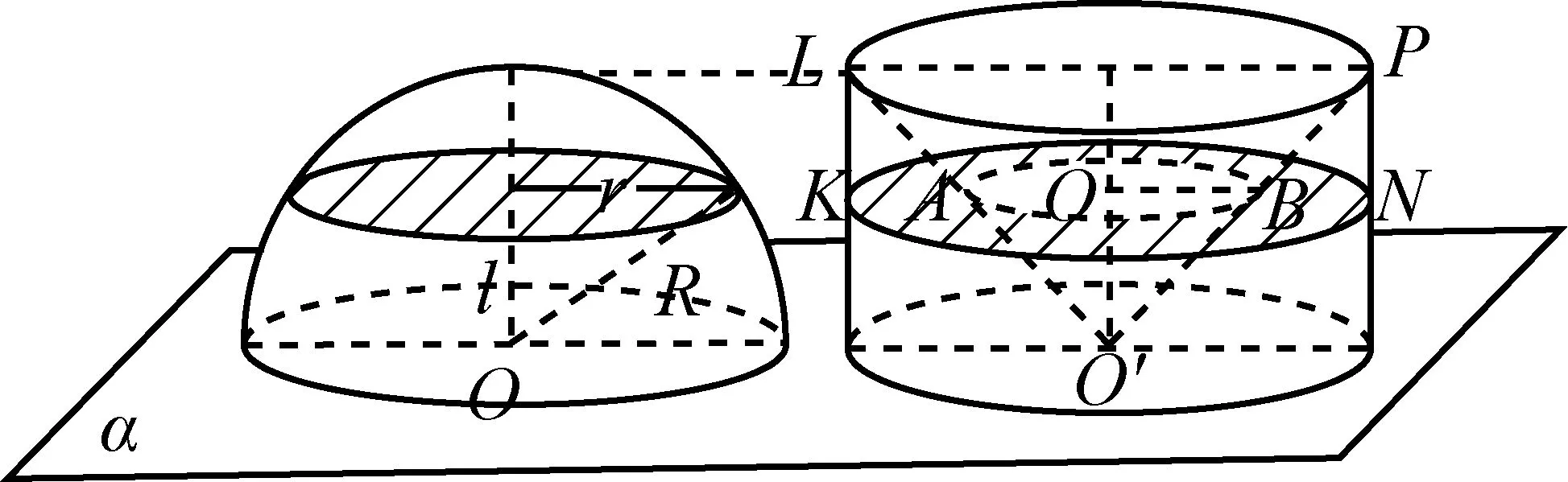
图16

设计意图应用“祖暅原理”可方便地推出柱体、锥体的体积公式，甚至反过来还能很容易地推出球体积公式，从而让学生体会到“祖暅原理”的好处，也进一步明白了中国古代数学的辉煌，增强了文化自信.

2.2.7 刘徽的启发

师：同学们，用祖暅原理推出球体积公式后，还能继续推导球的表面积公式.前面提到的数学家刘徽，为中国古代数学作出了很多贡献，比如在《九章算术注》中记载了他计算π近似值时首创的“割圆术”.

生17：初中老师讲过“割圆术”，把圆内接正多边形边数不断扩大，从而使正多边形的周长接近圆周长.

师：说得没错，见图17.刘徽将圆从正六边形割为正十二边形、正二十四边形，……，并说：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣！”这是非常伟大的创举，通过“化曲为直”和无穷小思想，得出了比较精确的圆周率值，可见刘徽在他那个时代就已经有了极限思想的萌芽.今天借鉴刘徽的方法来推导球表面积公式.

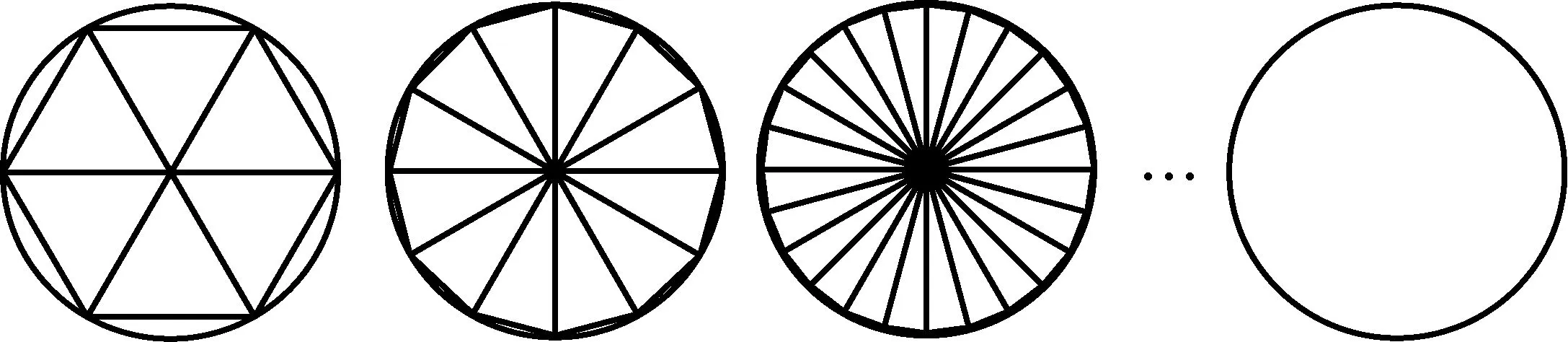
图17

生18：受刘徽“割圆术”的启发，可以将球的曲面化为平面，即“化曲为平”，分割得越细越接近于球的表面.

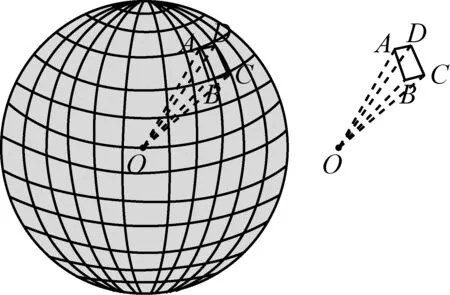
图18

生19：不妨给它取名为“割球术”！

师：这个名字取得好！看来大家对我国古代数学的成就已有所体会了.事实上，我们现在课堂上所学的每一个知识点，都是古代数学家前赴后继研究得出的结果，期间要经过几百年甚至上千年的艰辛历程，因此大家要珍惜这样的学习机会，努力将前人的智慧结晶学到，这正是大家在教室里进行学习的价值所在.

设计意图重新回到起点，从刘徽的二维“割圆术”升级到三维“割球术”，让学生明白“祖暅原理”的重要性，以加深理解中国古代数学家的伟大之处，培养了爱国主义，同时也让同学们懂得了在课堂学习的意义.

3 教学反思与启示

这是一节能完整体现学科育人的数学课，也是新教材“探究与发现”选学栏目中比较适合开发学科德育的内容之一.为了能综合分析课中所蕴含的育人元素，在教学反思时借鉴了栗小妮博士提出的数学学科德育分类框架[3]，从理性、人文、人格、责任四个方面进行分析.

3.1 数学学科德育要素分析

(1)理性精神的塑造

上课伊始，引导学生达成共识：高中阶段需要从理论上对公式进行推导，以体现数学学科的理性精神.于是在接下来的每个环节，都是从思维逻辑上严谨推导，而大量的图片或演示也只是为了帮助学生能较好地直观理解，所以整节课都充满着理性思考，培养了学生要辩证地分析问题和做事要有理有据的品德.

(2)人文精神的彰显

无论从刚开始提到的古希腊数学家阿基米德对数学的痴迷，还是中国古代数学家刘徽、祖冲之、祖暅一代代的薪火相传，孜孜不倦地研究，都可以让学生感受到人类追求真理过程中所遇到的困难和越挫越勇、勇往直前的精神.这种人文精神可培养学生坚韧不拔、刻苦钻研的探索意识以及面对挫折不要轻易放弃的学习态度.

(3)道德人格的熏陶

像刘徽这么一位对数学作出巨大贡献的中国古代伟大数学家，都能实事求是，非常谦虚地承认自己的不足，并希望后人超过自己的情怀，是值得每个人学习的.在这样的道德人格熏陶下，希望学生学会不以自我为中心，要善于向他人学习，以培养多从他人角度去思考问题的人生观与世界观.

(4)社会责任的培育

刘徽为了证明《九章算术》中的球体积公式而构造“牟合方盖”，再到发现其公式的错误后继续深入研究，直到穷尽一生也无法解决的经历，体现了数学家所具有的社会责任感和对数学研究认真负责的态度.同样，200年后的祖冲之、祖暅父子亦如此，他们耗尽一生心血也不放弃的使命感，可激发学生的爱国情感，能培养学生敢于担当、勇于承担的优秀品质.

3.2 选学内容的教学启示——学科德育的文化途径

通过对新教材“探究与发现”选学内容的开发设计与实践尝试，探索出让数学学科育人在课堂上落地的较好途径是融入数学文化.由此可得启示：将新教材中的选学内容加工开发成渗透学科德育的探究课，并从数学中的文化与文化中的数学两条途径来实施.

(1)数学中的文化途径

任何一个数学知识，在经过了萌芽、诞生、发展与完善的过程后才最后成熟的，而这也是古今中外数学家在一代又一代持之以恒的研究中取得成功的过程，期间的筚路蓝缕正是数学学科德育很好的育人素材.当然，数学中的主要文化载体是数学史，因此，一线教师需要对新教材中“探究与发现”“阅读与思考”等选学内容多查阅些数学史料，把背后隐藏着的育人元素通过重构设计落实到课堂.

(2)文化中的数学途径

学科文化源远流长博大精深，其涉及的范围甚广，包括社会生活、民族特征、科技进步、历史发展等方方面面，其中蕴涵的数学元素不胜枚举.数学家华罗庚说：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之迷，日用之繁，无处不用数学.”正因如此，新课标理念提出了跨学科整合，而新教材中一些选学内容与例习题都涉及到了各学科知识，一线教师可从文化中的数学途径多挖掘一些育人素材后落地课堂.

4 结语

数学课上渗透学科德育的育人要素，从而将立德树人落实在课堂教学上是新课标理念之一.笔者对“祖暅原理”这节选学内容进行了基于学科德育的设计，重走了一次发现“祖暅原理”的历史轨迹，以数学中的文化为实施途径，将育人要素这条主线贯穿始终，取得了不错的效果.当然，如何将新教材中的选学内容开展教学，学科德育究竟怎样融入较好，采用什么路径、策略实施有利于学生理解接受等也是见仁见智.笔者的这次实践探索，也是抛砖引玉，冀盼有更多一线教师进行开发尝试.