浅谈古代数学家刘徽的贡献及其思想

◎李秀艳

（唐山市路北区鹤祥实验小学 河北 唐山 063020）

早在古代时期，中国数学发展水平已经在世界上名列前茅，尤其是魏晋南北朝时期的刘徽，作为该时期杰出的数学家，他总结了大量的数学理论概念，为我国的数学思想和方法做出杰出贡献，并为中国传统数学理论发展奠定了坚实基础。其中，刘徽在《九章算术注》中总结了体积公理、十进分数理论、正负数定义及有关运算法则、方程的定义及其应用、刘徽原理以及割圆术等，这些数学方面的成就在中国古代历史中占据着重要的地位[1]。

一、古代数学家刘徽的贡献概述

我国古代数学家刘徽被称为中国历史上最伟大的数学家之一，并在世界数学历史上占有一定地位，其编写的《海岛算经》和《九章算术注》是我国历史上重要的数学著作。

诞生于东汉的《九章算术注》中主要注解了246个问题，比如几何图形面积计算、正负数运算、分数四则运算以及解联立方程等。这些成就远远领先于其他国家的数学水平，但是由于很多问题的解法非常原始，很多证明过程缺失。对此，刘徽进行了补充证明，有效的证明过程进一步展现出刘徽的创造力。同时，刘徽是世界上提出十进小数理论的人，同时对无理数立方根进行了有效表示。刘徽通过相应的转化能够对分数的平均值进行计算，其中关于代数方面的成就非常明显，刘徽正式提出加减运算法则和正负数概念，同时对线性方程组的计算方法进行完善。刘徽几何方面的成就也不容忽视，比如“割圆术”，能够通过圆周内正多边形的外切以及内接来对圆的周长和面积进行计算，并通过割圆术计算出圆周率的结果π =3.14。刘徽在《海岛算经》当中着重研究了“重差术”，并花费大量的精力对9个测量问题进行选编，从而创造出具有代表性、复杂性和创造性的题目。刘徽的数学思想非常敏捷，创新和应用的方法比较灵活，并积极倡导利用直观性和推理性解答数学题[2]。

二、刘徽的数学思想探究

（一）古代数学家刘徽的极限思想分析

世界上最早将极限思想应用到数学中的是我国数学家刘徽，比如刘徽在“阳马术、开放术、孤田术、割圆术”中都应用了极限思想。其中在方田章的23题中，刘徽利用割圆术对其圆田术进行注释，从而对圆周率以及圆的面积进行有效推算。同时，将正六边形的边数接到圆内来解析，其中，当正3×2n边形中的n为无限大时，圆的面积用其无限大时面积的极限来定义。基于该思想，刘徽通过圆内接正192边形来求圆的面积，最终获得的圆周率公式为

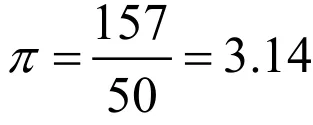
同时，刘徽通过圆内接正3072边形来求圆的面积，最终得到的圆周率公式为

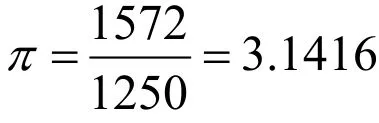
同时，刘徽在凌锥体积和弓形面积的解析中引用了“割圆术”。由此可见，刘徽经常引用极限思想来处理数学问题，并且应用非常广泛，对极限拥有很深的理解和认识[3]。

（二）刘徽的数形结合思想分析

刘徽曾自己单独开发了一种独特的数学方法，并通过系统发展衍生出“以盈补虚法”，同时又叫“出入相补原理”。该数学法和数学原理对古代的数形结合思想进行总结，以现代化数学思想和数学语言来解释，即将平面图形从一个地方移动到另外一个地方，则整个图形的面积不会发生变化。如果将一个图形划分为不同的小块，则这些划分完的小块的面积总和与原来的平面图形面积相同。由此可见，图形在移动前后的面积相同，且该原理和思想同时适用于立体图形。在“方田”的26题注中，刘徽通过变换等腰三角形，以矩形田的形式通过方田术来得到其最终的面积。从《九章算术注》中发现，刘徽的“出入相补原理”贯穿其中，由此证明刘徽的抽象逻辑思维能力和概括能力非常高，能够对实际问题的原理进行概括和解析，直观简明地展示一般原理的特征，有效联系不同的算法，最终获取更多的算法。

（三）刘徽的无限思想和辩证思想分析

首先，刘徽充分发挥自己的创造性，成功以数学方式证明无限过程的正确性，并通过阳马术注对相关的技巧进行展示。其中解释：“半之弥少，其余弥细，至细曰微，微则无形，由是言之，安取余哉？”通过无限分割，最终获得无形的东西。同时，在“割圆术”当中，刘徽通过将正多边形接入到圆内，通过圆内边数的增加，能够让多边形无限接近于圆。而刘徽的无厚可积观念以及不可分量构成几何图形占据了一定的地位，能够对一些体积和面积问题进行解析。其次，针对刘徽辩证思想的分析，其主要观点是具体问题要进行具体的分析和解决，不能够拘于一法来解决数学问题，比如《九章算术注》均输章节中的26题中刘徽认为存在两种解答方法，如何选择解答方法，刘徽的观点是“可随率益也”。

（四）刘徽的转化思想和逻辑推理思想分析

在实际运算过程中，刘徽通过转化思想来有效简化运算过程，比如在约分中，刘徽认识到“分之为数，繁则难用”，所以要进行约分，结果不会发生变化，刘徽对此表示：“设有四分之二者，繁而言之，亦可分为八分之四，约而言之，则二分之一也。”同时，刘徽对分数中的同值转换进行讲述。

刘徽对数学推理逻辑性比较重视，对《九章算术》中相关的数学概念进行定义和解释，并对不同问题之间所存在的逻辑关系进行分析。比如在“勾股”章节中明确表示勾股定理提出，主要是基于“将以施于诸率，故先具此术，以见其源也”。刘徽以严谨的逻辑论证了数学法则[4]。

三、结语

综上所述，数学家刘徽被称为中国历史上最伟大的数学家之一，其编写的《海岛算经》和《九章算术注》远远领先于其他国家的数学水平，创造出具有代表性、复杂性和创造性的题目，并积极倡导直观性和推理性解答数学题。在“阳马术、开放术、孤田术、割圆术”中都应用极限思想，经常用极限思想处理数学问题，对极限拥有深刻的理解和认识，单独开发了一种独特的数学方法，对古代的数形结合思想进行总结。刘徽的抽象逻辑思维能力和概括能力非常高，对实际问题的原理进行概括和解析，充分发挥自己的创造性，提倡具体问题要具体的分析和解决，不拘于一法来解决数学问题，通过转化思想来有效简化运算过程，从而有效论证相关的数学法则，为数学学科发展奠定坚实的基础。