一元二次方程的常见解题技巧分析

秦怡雯

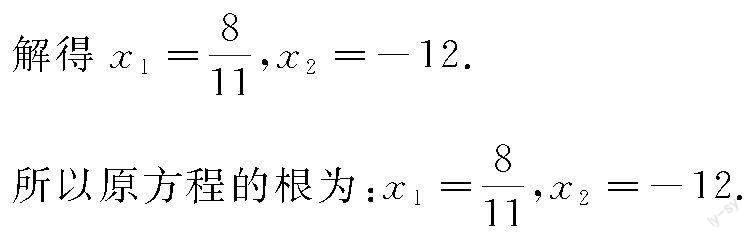
【摘要】一元二次方程的考查形式多种多样，相关的问题也都十分灵活.常规的一元二次方程求解方法有：配方法、公式法、因式分解法等.因此，在解决此问题过程中，要灵活掌握基本方法，以不同试题进行分析，优化解题思路.

【关键词】一元二次方程；配方法、公式法

一元二次方程是中学数学的一个重要内容，是历年中考考核的重点.它既有独立考查试题，也有广泛渗透到其他方面的综合考查.涉及的面非常广，是教学的基础也是重点.因此，掌握快速、精准地解题技巧显得尤為重要.

1 公式法

公式法是利用求根公式直接求解，把一元二次方程的各系数代入求根公式，直接求出方程的解.公式法是解一元二次方程的一般方法，又叫万能方法，对于任意一个一元二次方程，只要有解，就一定能用求根公式解出来[1].求根公式是用配方法解一元二次方程的结果，用它直接解方程可以避免繁杂的配方过程.解题思路大致为：①把方程化为一般形式；②确定a、b、c的值，计算b2－4ac的值；③当b2－4ac≥0时，把a、b、c及b2－4ac的值代入一元二次方程的求根公式，求得方程的根；当b2－4ac<0时，方程没有实数根.如以下例题所示.

例1 解一元二次函数方程：2x2－3x+1=0.

解 由2x2－3x+1=0

可知a=2，b=－3，c=1.

所以Δ=b2－4ac=9-4×2×1=1>0，

2 因式分解法

因式分解法适合解特殊的一元二次方程，例如缺少常数项的或者形如x2+（p+q）x+pq=0的一元二次方程适用因式分解，用因式分解法解一元二次方程首先要进行因式分解，使方程化为两个一次式的乘积等于0的形式，再使这两个一次式分别等于0，从而实现降次.解题思路大致为：①将方程的右边化为0，把左边因式分解成两个一次式的积；②令每个一次式都等于0，转化为两个一元一次方程；③解出这两个一元一次方程，它们的解即为原方程的解[2].具体解题思路和步骤如以下例题所示.

例2 解一元二次函数方程：4（3x+1）2=25（x－2）2.

分析 该例题首先将方程的右边化为0，移项将左边因式分解成两个一次式的积，令每个一次式都等于0，转化为两个一元一次方程，解出这两个一元一次方程，它们的解即为原方程的解.

解 4（3x+1）2=25（x－2）2，

移项得：4（3x+1）2-25（x－2）2=0，

［2（3x+1）］2-［5（x－2）］2=0，

［2（3x+1）+5（x－2）］·［2（3x+1）-5（x－2）］=0，（11x-8）（x+12）=0，

所以11x-8=0或x+12=0，

3 配方法

配方法适用于解任意的一元二次方程，其是把一般形式的一元二次方程：ax2+bx+c=0 （a≥0）左端配成一个含有未知数的完全平方式，右端是一个非负常数，进而可用直接开平方法来求解.解题的大致思路为：①移项、二次项系数化成1；②配方，开平方进行运算即可.具体解题思路和步骤如以下例题所示.

例3 解一元二次函数方程：2x2－4x－m=0（m≥2）.

分析 该例题首先根据已知条件m>-2即可.移常数项，两边配上一次项系数一半的平方，转化成（x+m）2=n的形式，由x>0，可知方程有实数根，最后开平方进行运算即可解出一元二次方程.

解 2x2－4x=m，

所以方程有实数根.

例4 解一元二次函数方程：x2+2x－4=0.

分析 该例题首先移常数项，两边配上一次项系数一半的平方，转化成（x+m）2=n的形式，最后开平方根进行运算即可解出一元二次方程.

解 x2+2x－4=0，

x2+2x+（1）2=4+（1）2，

（x+1）2=5，

4 结语

根据上述不同的求解一元二次方程问题的例题分析，可以得到公式法、因式分解法以及配方法求一元二次方程的方法.针对不同类型问题，采取相对应的解题方法进行解答.在解题过程中，同学们应加强对问题条件的分析应用，借助已知条件和相关性质去灵活解答，以此提高解题的效率，让同学们在考试中得心应手，同时也希望同学们谨记各部分的注意事项，记住各种方法的适用范围，以便在考试中能够灵活运用，避免出现错误.

参考文献：

［1］唐寿.浅谈初中数学一元二次方程的解法及其应用[J].基础教育论坛， 2019（20）：40-41

［2］李晴.初中数学“融错”教学智慧分享策略的研究——以“一元二次方程的解法复习”为例[J].上海中学数学， 2021（9）：35-37.