圆类综合题的构建剖析与探究总结

方国贝

【摘要】圆类综合题在中考中十分常见，也是圆类知识考查的重要方式.探究剖析时需要立足考题开展考点分析，结合所学知识进行逐步剖析，在此基础上总结方法，形成策略.本文结合2022年江苏省各市的中考题开展圆类综合题的解法探究，与读者交流学习.

【关键词】圆；三角函数；面积割补

圆是特殊的几何图形，也是初中阶段需要重点掌握的图形，与圆相关的综合问题在中考中十分常见，命题形式多样，解析突破需充分利用圆的性质，结合关联知识逐步剖析，下面来深入探究圆类综合题.

1 圆与三角函数

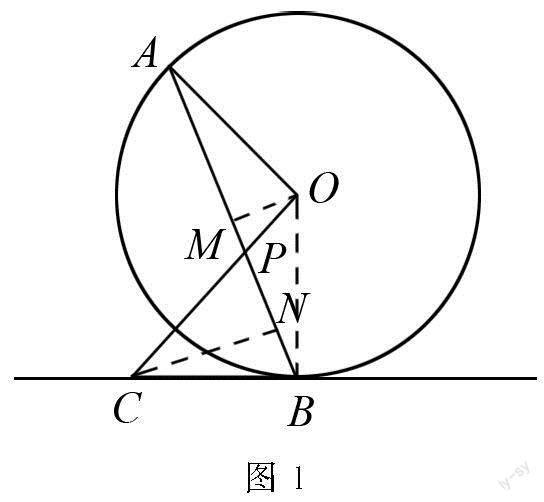
例1  （2022年扬州市中考卷第25题）如图1所示，AB为⊙O的弦，OC⊥OA交AB于点P，交过点B的直线于点C，且CB=CP.

（1）试判断直线BC与⊙O的位置关系，并说明理由；

解析 （1）简答，直线BC与⊙O为相切关系.

（2）分别作OM⊥AB，交AB于点M，再作CN⊥AB，交AB于点N，如图1所示.

分析可知AM=BM，

因CP=CB，AO⊥CO，可推得∠A=∠PCN=∠BCN.

评析 上述考题的第（2）问将圆与三角函数相结合，解析时构建直角三角形，利用三角形的边角关系来求线段长.锐角的三角函数是初中较为特殊的知识，需依托直角三角形来转化，其破解策略需要学生灵活掌握，既能转化三角函数值条件，也可利用直角三角形的三边关系求值.

2 圆与图形割补

例2 （2022年宿迁市中考卷第25题）如图2，在△ABC中，∠ABC=45°，AB=AC，以AB为直径的⊙O与边BC交于点D.

（1）判断直线AC与⊙O的位置关系，并说明理由；

（2）若AB=4，求图中阴影部分的面积.

解析 （1）略；

（2）记BC与⊙O的交点为M，连接OM，如图2所示，

S阴影=S△ABC- S△BOM-S扇形AOM，

分析可知∠AOM=2∠ABC=90°，∠BOM=90°，

⊙O的半径OA=2.

所以S阴影= 8－2－π=6－π.

评析 上述考题的第（2）问求阴影部分图形的面积，开展图形面积割补是突破的关键，即将阴影图形视为是三角形与扇形的分割与组合.面积割补法是求解不规则图形面积问题的有效方法，解析时需灵活分割图形，将其拆解为规则图形，然后基于图形关系构建面积关系.

3 圆与网格探究

例3 如图3所示的网格中，已知小正方形的边长均为1，对应的顶点A、B、C、D、M均为格点.

操作探究 在探究课上，同学在图3的网格中，使用无刻度的直尺画了两条互相垂直的线段AB和CD，两线的交点为P，并给出部分推理过程，请进行补充：

解 在网格中取格点E，作出两个直角三角形，分别是△ABC和△CDE.

在Rt△CDE中，   ，

所以tan∠BAC=tan∠DCE.

所以∠BAC=∠DCE.

由于∠ACP+∠DCE=∠ACB=90°，

則∠ACP +∠BAC=90°，可推知∠APC=90°，则AB⊥CD.

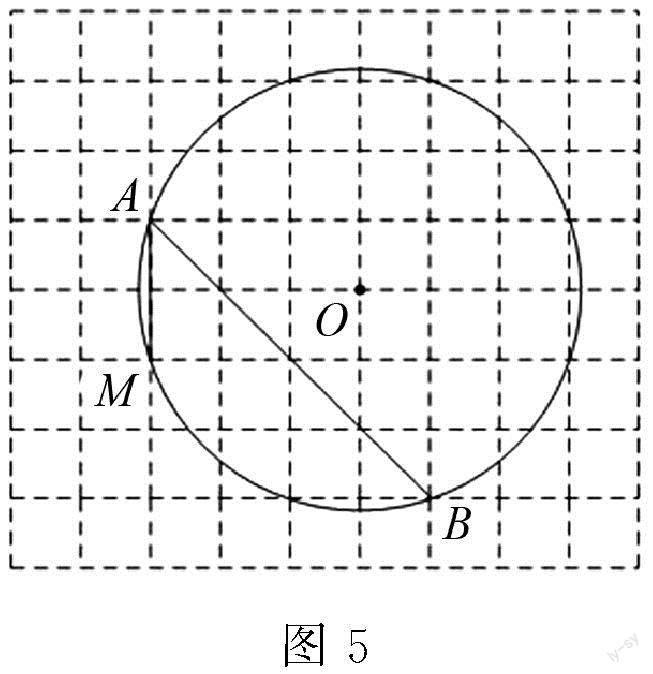
（2）拓展应用 如图5所示，以格点O为圆心作圆，请仅用无刻度的直尺，在弦AB上作出点P，使AM2=AP·AB，请写出详细的作法，并加以证明.

（1）略；

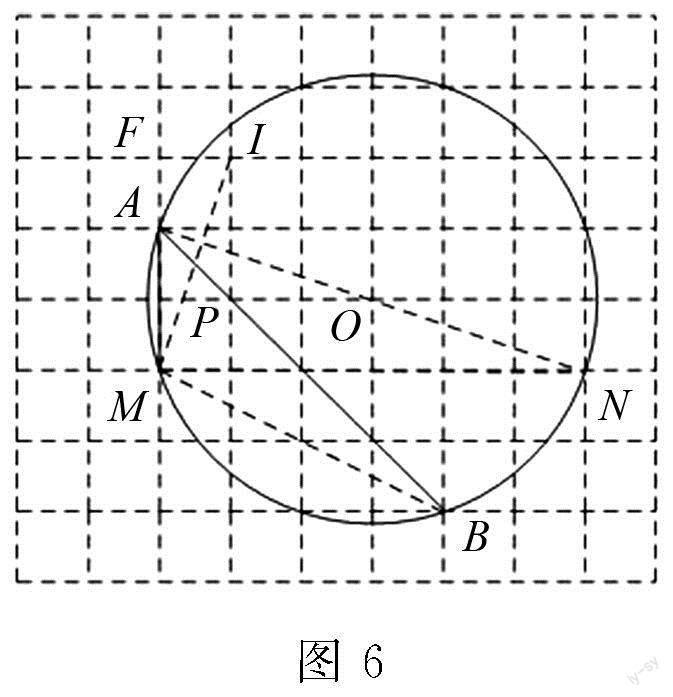
（2）取格点I，连接MI，与AB交于点P，如图6所示，则点P为所求点，证明如下.

作直径AN，再连接BM和MN，如图6，

整理可得AM2=AP·AB.

4 结语

总之，上述所探究的三大圆类综合题，分别从三角函数、图形割补、网格综合角度进行命题构建，剖析关联、生成模型、结合所涉及知识分步突破是解题的关键.圆类综合题的探究剖析，需要关注问题特征、知识考点、解析过程，从类型问题中总结破题方法，形成解题策略.