垂径定理在解圆内三角形问题中的应用

冒奕敏

【摘要】垂直于弦的直径平分弦，并且平分弦所对的两条弧.垂径定理是初中数学几何中解圆与三角形问题中经常运用到的一条定理，既考查了学生的抽象思维，也考查了学生的数形结合能力，要求学生能够在圆的半径、弦心距、弦的一半中选择正确的线段，构造出直角三角形，然后结合勾股定理，求出所需的线段长度.本文列举三道例题，介绍垂径定理在解圆与三角形结合的线段长问题中几种常见的考查方式，并给出分析思路和解题过程，希望可以帮助学生们对垂径定理的应用有更深的了解，对抽象思维和数形结合方法有更全面的认识.

【关键词】圆；三角形；垂径定理

在运用垂径定理计算圆与三角形的问题中，计算或证明圆心到弦的垂线段、弓高、半径或弦长时，通常需作出圆心到弦的垂线段，垂足就是弦的中点，再利用半径、弦心距和弦长的一半，构造出直角三角形，结合勾股定理进行求解.

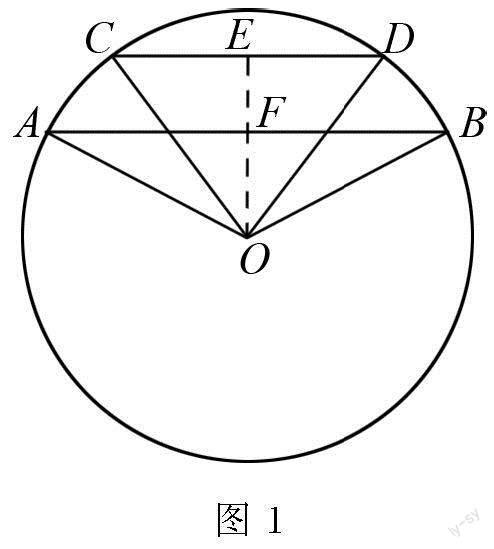
例1 已知圆O的半径长为26，圆内有AB和CD两条弦，AB∥CD，且AB的长为48，CD的长为20，求弦AB与弦CD之间的距离为多少？

解题思路 本题要求计算的是两弦之间的距离，证明圆心到弦的垂线段、弓高、半径或弦长时，首先要根据题目已知条件和所求问题，作出正确的辅助线，通常作圆心到弦的垂线段，以半径、弦的一半、弦心距为三边构造一个直角三角形，再利用勾股定理即可进行求解.注意，本题需要考虑弦AB、CD在圆心的同侧还是异侧.

解 因为弦AB与CD相对于圆心的位置有两种可能，所以需要分类讨论.

第一种情况，当两弦在圆心的同侧时，如图1所示.

过点O作OE⊥CD于点E，交AB于点F，

因为AB∥CD，

所以EF⊥AB，

则线段EF的长等于弦AB与CD之间的距离.

CD=20，

所以DE=12CD=10，

由题目可知OD=26，

在Rt△OED中，由勾股定理有

在Rt△OFB中，由勾股定理有

所以EF=OE-OF=14.

第二种情况，当两弦在圆心的异侧时，如图2所示.

过点O作OE⊥CD于点E，延长EO交AB于点F，

因为CD∥AB，

所以EF⊥AB，

则线段EF的长等于弦AB与CD之间的距离.

在Rt△OED中，由勾股定理有

在Rt△OFB中，由勾股定理有

则EF=OE+OF=34.

故弦AB与弦CD之间的距离为14或34.

例2  如图3，线段OD为圆O的半径，AE为圆O的直径，AB是圆O的弦，且长度为16，OD垂直AB交AB于點C，CD的长等于4，求线段CE的长为多少？

解 如图3，连接BE，设圆O的半径为x，

有OC=OD-CD=x-4，

因为OD⊥AB，

在Rt△AOC中，根据勾股定理有

AO2=AC2+OC2，

即x2=82+（x-4）2，

解得x=10，

则OC=x-4=6，

因为AC=BC，AO=OE.

所以BE=2OC=12，

因为AE为直径，

所以∠ABE=90°，

在Rt△CBE中，

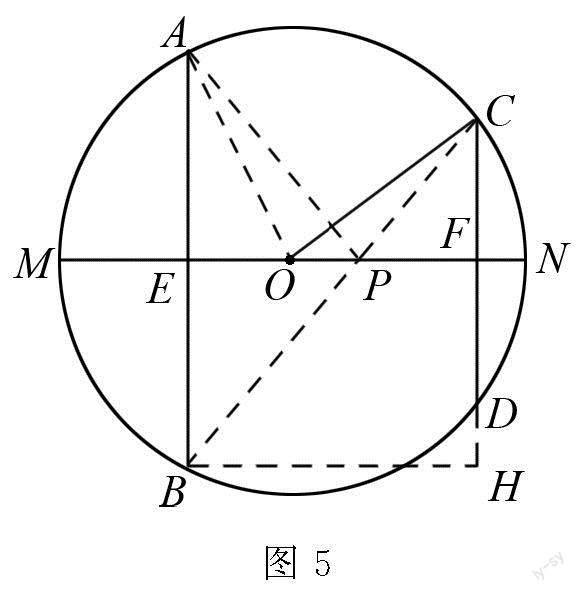
例3 如图4所示，圆O的直径为20，线段AB和CD分别为圆的两条弦，其中AB的长为16，CD的长为12.MN为圆的直径，AB与MN相互垂直，相交于点E，CD与MN相互垂直，相交于点F，点P为线段EF上的任意一点，求线段PA与PC长度之和的最小值为多少？

解题思路 求圆中的线段的最短长度，或者两点之间的最短距离问题，需要运用到转化的思想.因为圆是一种典型的轴对称图形，以直径为对称轴，圆上任意一点的对称点都落在圆上，因此作出其中一点关于直径的对称点，把分散的线段转化到同一条直线上，即根据“两点之间线段最短”的原理把最短距离转化为弦长，就可以求得这两条线段之和的最短长度.

解 如图5所示，连接BC，交MN于点P，连接AP，过点B作MN的平行线交CD的延长线于点H.

根据垂径定理可知AP=BP，

所以PA+PC=BP+PC，

因此，当点B、P、C三点共线时，线段PA与PC的长度之和取得最小值，

因为MN是圆O的直径，AB⊥MN，CD⊥MN，

所以AE=BE=8，CF=DF=6.

易知四边形EBHF为矩形，

所以FH=EB=8，

CH=CF+FH=14，

连接OA，OA=10，

连接OC，同理得OF=8，

所以BH=EF=OE+OF=14，