“互联网+”背景下数学建模教学设计研究

摘要：本文将围绕传统数学建模课程教学方式存在的不足展开分析，阐述“互联网+”背景下数学建模教学设计路径，以帮助教师适应互联网时代下数学教学的变革，以学生为主体，制作高质量的教学内容，组织有意义的课堂提问环节，使学生容易理解相对抽象的知识点，培养学生的建模意识，提高其计算能力，最终形成数学核心素养。

关键词：中职院校；数学建模；互联网时代

一、引言

数学建模是将实际问题与数学模型结合，并通过对数学模型的求解解决实际问题的思考方式。良好的数学建模教學可以帮助学生养成数学核心素养，并运用数学解决实际问题。但根据实际调查显示，部分学校在数学建模课程教学方式上仍有待提升。

二、传统数学建模课程教学方式分析

尽管我国目前尚没有固定的方法用于数学建模解决实际问题，但解决问题时建立的数学模型的过程却基本一致，包括模型准备、假设、建立、求解与修改。数学建模本身属于一门实践性极强的课程，主要运用数学知识以及计算机设备，探究问题的形成原因，能够帮助学生运用已经掌握的知识解决生产、生活中的问题。但许多学校在开展数学建模教学过程中仍存在以下问题。

一是学生的课堂表现积极性不强，缺少对数学建模的学习兴趣，教师与学生之间的互动和交流不够频繁。许多教师仍采用单向的黑板教学，过于注重学生的知识理论吸收，并要求学生认真记录模型的求解方法。这种教学模式相对枯燥，既不利于学生完成自我展示，也难以调动学生的学习热情。

二是数学建模与学生现有知识的关联度较低。在难度设置上，数学建模应尽可能采取通俗的例子，加深与学生日常生活的联系，并以生活化问题、社科类问题、专业背景应用问题为主。同时，教师本身也要加强信息技术的运用，采用互联网手段更好地收集教学资源。

三、“互联网+”背景下数学建模教学设计路径分析

（一）设置好建模问题

问题本身是数学教学实施的核心载体，通常来说，发现问题远比解决问题更重要，因此，在数学建模教学过程中，教师应优先确定主题，不可单纯通过编写应用题、讲解应用题，由学生模仿解题套路来实现数学教学，而是要保证数学建模活动能够充分指引学生关心社会、学会交流。为此，本文更倾向于从当前社会热点问题中找寻能够用于数学建模的题材，要求教师能够筛选出与中职学生日常生活更加贴近的内容，符合其认知水平，避免背景过于复杂，并在建模求解过程中，使学生无需学习大量新知识，便可着手解决热点问题。

笔者将以新冠疫情对城市生产、生活产生的冲击作为研究对象，并抛出以下问题：

问题1，由于新冠疫情的影响，导致世界杯延迟进行，此类问题是否能够利用数学建模进行预测？若世界杯正常开展，运动员的比赛成绩又是否会受到影响？

问题2，在线下复课后，中职院校的食堂管理必然会承受更大的挑战，是否可以借助数学知识来设计切实可行的分流方案。

问题3，为了更好地消除疫情带来的不利影响，推动城市经济发展，我国各地区均开展了发放消费券的活动，若对此问题采用数学关联，是否可以对消费券的实际作用产生一个简单地预判。

上述问题的开放程度较高，能够使学生从多个层面实现数学知识的关联，帮助学生激发想象力，开展数学探究活动。根据研究显示，问题3的应用价值更高，因此，笔者最终决定将其作为数学模型的设计背景，在实现数学建模时要注意，选取的问题必须源自生活，尽可能满足学生的好奇心与求知欲，问题的难度要进行适当调整，确保既能实现学生的集中讨论，也能保证学生的深度参与，从而起到调动学生参与建模活动热情的作用，同时，问题本身要具有一定的挑战性，有助于学生展示个性化见解[1]。

（二）合理设计教学模式

在选取适合的建模问题后，教师要在教学过程中把握以下两个教学方向：一是要让学生亲身体验数学建模的设计过程；二是教师要将学生作为教学主体，打破以往的机械式解题训练，围绕建模问题，带领学生深入探究。教师主要负责必要时指引学生梳理解题思路。

经过长时间分析，笔者最终确定将数学建模设计划分为以下几个环节：

1.设置问题情境

以某直辖市作为研究对象，为了更好地促进社会经济水平的提升，该城市开展了“乐游乐享”的消费节活动，累计向市民派发近1亿元消费券，用于激发城市居民的消费热情，推动零售、旅游等行业的复苏。在数学建模设计环节中，教师与学生对三个建模问题展开深入探究，分析各自的优势和劣势后，决定将问题3确立为研究主题，并进一步挖掘建模活动的实际意义。

2.问题理想化

首先，教师需组织学生收集与消费券发放有关的数据信息，例如发放原则、使用效果等，然后进行数学化处理，教师可以将学生分成小组，探究数学关联性，引导学生积极参与教学活动，让学生自主发表相关建议与意见。教师还要指导学生讨论消费券的使用状况，预判消费券的使用会产生多大的消费额，借助关联函数的拟合，引导学生突出主要因素，进一步将实际问题转化为统计问题[2]。

3.打造数学模型

教师应当给予学生充足的学习时间以及数据收集时间，通过问卷调查、互联网搜索等方式获取与消费券有关的内容，并创建模型进行求解。在此过程中教师要优先明确学生的实际需求，督促学生做好调查研究，鼓励学生自主查阅相关资料和检索已有成果，通过小组合作的形式集思广益，初步拟定问题解决的思路与方案，并判断相关计划的可行性与可靠性，之后定期组织学生分析建模情况，让学生逐个展示数学建模成果，并提供针对性地指导。

4.模型呈现

笔者将以某中职院校作为研究对象，根据调查显示，该学校的学生建模小组共做出4个模型，教师带领学生将所得成果最终提升为具有理论意义的实际结论。

模型1，消费券以及消费者意愿的检验，通过从互联网上找寻的某地区消费意愿调查显示，有消费券且影响消费意愿的人数为409人，有消费券但不影响消费意愿的人数为153人，无消费券且影响消费意愿的人数为376人，无消费券且不影响消费意愿的人数为10人。根据计算公式：

由于97.5＞10，证明几乎100%的把握确定消费券与消费意愿相关，因此发放消费券能够刺激城市居民的个人消费意愿，具有良好的消费效果，可以保持高水平的消费热度，证明此项措施具有实际意义。

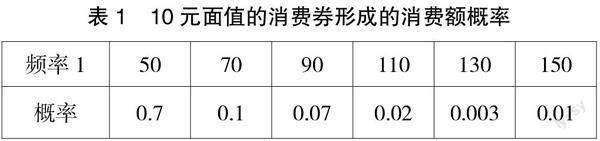
模型2，利用频率实现概率的估计，预测各面值消费券产生的消费金额。比如采用10元面值的消费券所形成的消费额概率分布表现为：

计算公式为：

数学期望1=50×0.7+70×0.1+90×0.07+110×0.02+130×0.003+150×0.01=58.8

根据计算可知，采用10元面值消费券所形成的消费额数学期望为58.8元，而采用20元面值消費券时形成的消费额概率分布则表现为：

计算公式为：

数学期望2=90×0.6+110×0.2+130×0.04+150×

0.04+170×0.02+190×0.06=106.2

根据计算可知，采用20元面值消费券所形成的消费额数学期望为106元，而采用50元面值消费额所形成的消费额概率则表现为：

计算公式为：

数学期望3=250×0.7+350×0.1+450×0.05+550× 0.03+650×0.01+750×0.01=296.7

根据计算可知，采用50元面值消费券所形成的消费额数学期望为296.7元，而采用100元面值消费券形成的消费额概率则表现为：

计算公式为：

数学期望4=500×0.7+700×0.1+900×0.08+1100×

0.03+1300×0.01+1400×0.01=600.4

根据计算可知，采用100元面值消费券所形成的消费额数学期望为600.4元。

综上所述，由于各类面值对消费金额产生的放大影响存在一定的差异性，其中放大倍数最为显著的为100元面值，而放大倍数最小的则表现为20元面值。因此可以确定，该城市在发放1亿元消费券后，所形成的消费额期望值大约在6亿元，而最低则5亿元。

模型3，对该地区的消费券使用方向进行统计后显示，消费券流向最多的行业为餐饮业与超市，民众更想要外出就餐，感受城市烟火气息，证明地方政府防疫效果显著，居民的信心正不断提升，服务消费更受大众喜爱。同时，餐饮行业本身具有极强的带动作用，能够推动产业链上其他行业的消费水平上涨，引发乘数效应。

模型4，消费券与消费金额的函数拟合，根据调查问卷的数据制作消费券金额与消费金额的散点图后发现，消费额大约是消费券金额的5倍，即1亿元消费券可产生5亿元的消费额，由此可得出结论，即消费券活动能够推动消费回补。

5.模型修正

模型1中，消费券需要市民自愿申领，并非随机发放。因此，根据该原则分析消费券的申领数量对市民的消费次数影响情况会存在一定的限制。同时，在开展消费券与消费意愿的检验时，还需完成其他变量的检验，例如判断性别是否与消费意愿存在关联，此外，由于样本容量相对较少，问卷发放群体相对集中，因此会对预测结果的精确性产生影响。

模型2中，由于涉及部分隐私，所以统计的数字都是范围，只能获取估算的效果，并且各类面值对消费金额的作用也不统一，是否可以利用官方数据了解各类面值消费券的实际发放比例仍有待进一步探究；若可以，则要充分结合发放比例，以提高模型数学期望的精

确性。

模型3中，消费券在超市中的使用应实现细化处理。如果消费券更多地集中在生活必需品的采购上，会对消费券的乘数效应产生一定影响；如果消费券更多地应用在产业链相对较长的区域，则乘数效应会更加明显，从而达到提高统计结果价值的作用。

模型4中，只是简单地实现了消费券金额与消费额之间的线性拟合，并未将非线性拟合的影响，因此也无法确定非线性拟合的实际效果以及预测意义。同时，在模型分析中可以发现，1亿元消费券预计可收获近5亿元的消费额，预测目标与给定的数据区间相隔较远，导致数据预测结果的应用价值大打折扣。虽然能够得到10万元消费券所产生的消费额最优，但需要认识到统计不存在绝对的正确，更应该注重标准的设置，如果标准本身存在一定差异性，结论自然也不会统一。这样有助于培养学生的数学建模素养，提高学生的数据分析能力，有利于学生采用统计知识解决实际问题[3]。

（三）实践反思

首先，教师要注重学生的学习感受，更多地站在学生视角来看待教学应用效果，同时要求教师充分发挥指引者角色，主导课程的推进，并善于找出实际生活中存在的数学关联，启发学生感受建模的魅力。为此，教师要丰富自身的理论知识，提升实践经验，做到坚持学习、留心观察、善于发掘，可以以熟悉的标准作为切入点，开发更优质的情境和更有价值的问题。

其次，教师要指导好学生进行选题工作，许多中职学生的数学知识储备不够充足，缺少研究经验，经常会出现遇到问题时采用的研究方法不够高效，受到主观条件的严重限制。也有部分学生在选择问题时会受到不可测因素多、涉猎面宽泛等客观因素的影响，导致选取的问题意义较低，并对选择的问题难度缺少准确认知。因此，教师在指导学生进行选题时，不要过于注重问题的实际难度，而要尽可能选择自己了解的、擅长的、不可测因素较少的问题。

最后，学生应当作为数学建模教学的主体，深度参与数学建模，并展现数学建模的活动特性，不再依赖教师讲题、学生模仿练习的传统教学模式，而是更多地采用小组交流的方式，保证人人动脑、人人参与，并由教师提供平台，使学生能够自由地展示自我。同时，教师在小组分配时要考虑到不同学生之间的个体差异性，以便学生能够在组内可以自主交流，使学生在展示自我的过程中获得自信与成就感，并产生对研究数学的兴趣[4]。

四、结束语

综上所述，通过对传统数学建模课程教学方式存在的不足之处开展分析讨论，提出了一系列适应“互联网+”背景下的数学建模教学设计路径，包括设置好建模问题、实现问题的理想化、打造数学模型、完成模型的呈现与修正等，以此帮助中职院校教师充分发挥数学建模的应用优势，更好地解决实际问题，帮助学生建立良好的数学素养。

参  考  文  献

[1]蔡璐，李新菊，韩祥临.数学建模核心素养层级下提升数学思维品质的教学探究[J].教学与管理，2022（36）：99-103.

[2]黄华，王飞，宋艳萍.基于“项目驱动+以赛促学”教学模式的数学建模教学探索与实践[J].高教学刊，2022，8（17）：108-111.

[3]黄慧青，温坤文，胡汉章.翻转课堂在地方院校数学建模教学中应用的可行性探讨[J].高教学刊，2022，8（01）：96-99.

[4]马志宏.将课程思政融入大学数学建模教学  提升学生综合素养的研究与实践[J].天津农学院学报，2021，28（04）：101-104.

侯万超（1993-），男，汉族，江苏连云港，本科，助理讲师，研究方向：应用数学。