例谈椭圆中的蝴蝶模型
卢恩良
(江西省九江市第三中学,江西 九江 332000)
圆锥曲线中的定点、定值问题备受命题人青睐,其中以椭圆为载体的试题更是屡见不鲜.椭圆中有一类定点、定值问题,因所涉图形酷似糊蝶,故称“蝴蝶模型”.本文举例说明“蝴蝶模型”在定点、定值问题中的应用.
1 定点问题
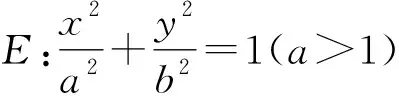
(1)求E的方程;
(2)证明:直线CD过定点.


图1 2020年全国Ⅰ卷理科20题

设C(x1,y1),D(x2,y2),




整理,得
3x2y1-9y1=x1y2+3y2.
将x2=ty2+m,x1=ty1+m代入,得

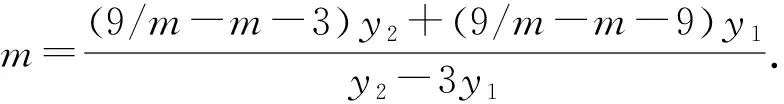








(1)求a的值;
(2)设AF,BF的延长线分别交椭圆于D,E两点,当k变化时,直线DE是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.

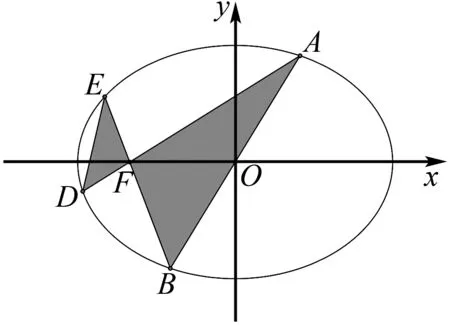
图2 例2解析图






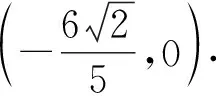
评析本题破解关键有三点.第一是敢于联立直线AF与椭圆方程,不畏繁杂的运算;第二是通过类比代换由点D坐标得到点E坐标;第三是写出直线DE方程,令y=0,朝着目标大胆运算下去.

变式题在例2模型的基础上,将四边形对角线所过定点由特殊的焦点变为一般的点N,边AB不再过原点O而是一般的点M.下面对变式问题进行解答.







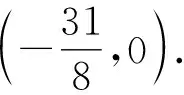
通过以上两个例题和一个变式题,我们感受了椭圆蝴蝶模型中的定点问题.通过进一步研究,我们可以把椭圆蝴蝶模型中的定点问题作一般化推广,得到以下两个命题.


椭圆中的蝴蝶模型内涵丰富,值得深入研究.它不仅涉及直线过定点问题,还涉及到与斜率有关的定值问题.下面通过两个例题来发现其中规律.
2 定值问题



图3 例3解析图
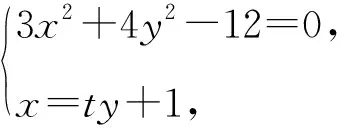
设D(x1,y1),E(x2,y2),

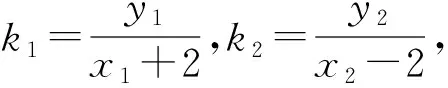


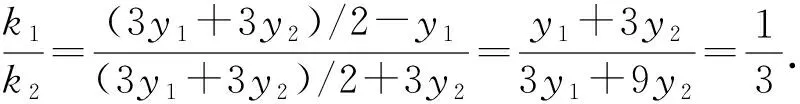
评析先猜后证是解决定点、定值问题的典型方法,体现了解决数学问题的思维过程,有助于明确解题方向和目标.


(2)若M为椭圆C上的动点(异于A,B),连接MF1并延长交C于点N,连接MD,ND并分别延长交C于点P,Q.设直线MN,PQ的斜率分别为k1,k2,试问是否存在常数λ使得k1+λk2=0?若存在,求出λ;若不存在,说明理由.
下面主要对第(2)问进行解答.

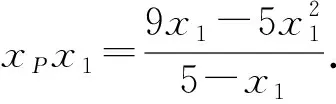





把例3和例4进行一般化,我们可以得到下面两个命题.


文中通过几个典型例题介绍了椭圆中蝴蝶模型的定点、定值问题的处理办法.仔细分析发现,该模型本质上体现了椭圆内接四边形的一些性质结论.文中四个命题将例题中的蝴蝶模型作了一般化的推广,仅供同学们了解,教学重点依然是通过常规方法,训练运算能力,提升数学核心素养.

