基于鞅驱动的时滞倒向随机微分方程最优控制

周 敏,颜 瑞,李志民

(安徽工程大学数理与金融学院,安徽 芜湖 241000)

0 引言

线性倒向随机微分方程由BISMUT[1]首次提出,方程一般化面临的一个问题是要解决方程的存在唯一性,此问题困扰学界很长时间.PENG[2]在利用线性倒向随机微分方程研究随机最大值原理问题时发现,解决强制性是推动倒向随机微分方程的关键.随后,PARDOUX和PENG[3]提出了一般形式的倒向随机微分方程,解决了这个倒向随机微分方程的研究瓶颈问题,PENG[4-6]在后期的系列工作建立了倒向随机微分方程理论体系.

PENG的工作推动了倒向随机微分研究的蓬勃发展,后继学者围绕如何解决方程中的生成元的结构和扩散部分开展研究,产生一系列成果.TANG和LI[7]讨论了布朗运动和泊松过程混合驱动的倒向随机微分方程,KAROUI等[8]研究由一般鞅驱动的倒向随机微分方程.王湘君[9]研究了以连续局部鞅为干扰源的倒向随机微分方程,在系数满足Lipschitz条件下证明了其解的存在唯一性.李娟[10]在此基础上研究了以一般鞅为干扰源的倒向随机微分方程,对经典的倒向随机微分方程进行实质性推广,得到了其解的存在唯一性.一些学者尝试弱化终端条件和生成元的Lipschitz条件来推广PARDOUX和PENG的结论,FAN等[11]得到了非Lipschitz条件下倒向随机微分方程解的存在唯一性;程中华[12]得到了非Lipschitz条件下和局部Lipschitz条件下由连续局部鞅驱动的倒向随机微分方程的解的存在唯一性,并得到了其比较定理.DELONG等[13]考虑生成元在时间上可以依赖于过去的一个解的值,用一个时间延迟函数加权,给出了时滞倒向随机微分方程的概念.CHEN等[14]考虑生成元不仅取决于瞬时状态,还通过时滞参数取决于过去的状态,利用带时滞生成元的倒向随机微分方程和超前随机微分方程之间的对偶性,证明了这两类方程解的存在唯一性,导出了最大值原理的充要条件.

倒向随机微分方程理论和方法逐渐被应用在金融产品的定价中,冯莎莎等[15]总结了期权定价模型,同时利用倒向随机微分方程推导期权定价公式.马玉东[16]通过对倒向随机微分方程进行保险定价公式的合理改进,加入了公司营业费用率和未决赔款准备金比率的参数调整,使之更加符合保险公司的实际经营情况.徐铭浛[17]利用倒向随机微分方程求解连续支付红利的期权定价,苗杰[18]用BSDE理论得到了可分离债券价格所满足的倒向随机微分方程,得出了可分离债券价格的显式公式.在CHEN等[14]的研究中,方程是在布朗运动驱动下的倒向随机微分方程,具有较强的限制条件,而在实际问题中尤其是在金融问题中,布朗运动往往不是刻画股票价格过程的理想工具[19].为此,本文考虑了更加一般的情况,对驱动过程进行推广,将连续鞅驱动的倒向随机微分方程与时滞结构结合起来,考虑由连续鞅驱动的时滞倒向随机微分方程和与之对偶的连续鞅驱动的超前随机微分方程,利用解的存在唯一性,时滞倒向随机微分方程生成元可以依赖过去的状态,从而可用于股票价格具有时滞效应的期权定价、保险费率计算等,在决策和控制中亦有应用的可能.

1 准备知识

其中,y(t)是一个-适应的Rn-值的过程.当n=1时上式简记为LM.

其中,z(t)是一个-可料的Rn-值的过程.当n=d=1时上式简记为

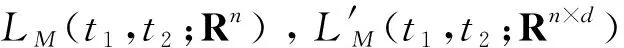
考虑以下时滞倒向随机微分方程(BSDE):

(1.1)

假设方程系数满足如下条件:

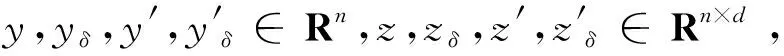
考虑以下形式的超前随机微分方程:

(1.2)

其中,对于∀t∈[0,T],r∈[t,T+δ],有

且满足下列假设:

(H2.1)存在一个常数C3>0,使得对于所有的t∈[0,T],x,x′∈Rn,ζ(·),ζ′(·)∈LM(t,T+δ;Rn),r∈[t,T+δ],有

2 解的存在唯一性

对于由方程(1.1)确定的具有时滞结构的由鞅驱动的倒向随机微分方程,给出如下定理.

其中,a(β,s,t)=exp(β(〈M〉s-〈M〉t)).

令

(y(·),z(·))=Φ[(Y(·),Z(·))],

(y′(·),z′(·))=Φ[(Y′(·),Z′(·))],

从而有

于是有

注意到,

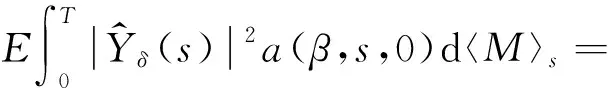
同理,

只要δ足够小,就能保证K(C2,L,δ,α,β)<1,即

(y′(·),z′(·))=Φ[(Y′(·),Z′(·))]≤K(C2,L,δ,α,β)[(Y′(·),Z′(·))].

因此Φ在范数‖·‖β下就为一个压缩映射,由不动点定理可知,定理2.1得证.

证明 类似于定理2.1的证明,定义以下范数,在Hilbert空间LM(0,T+δ;Rn)中构造压缩映射:

其中,a′(β,s,t)=exp(-β(〈M〉s-〈M〉t)).

定义映射I:LM(0,T+δ;Rn)⟹LM(0,T+δ;Rn),使得I[X(·)]=x(·).对于任意的X(·),X′(·)∈LM(0,T+δ;Rn),记

I[X(·)]=x(·),I[X′(·)]=x′(·),

其中,

由b,σ满足(H2.1),得到

于是,

注意到,

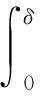
因此I在范数‖·‖β下为一个压缩映射.由不动点定理可知,定理2.2得证.

3 解的最优控制

在金融领域,具有延迟盈余的养老金、具有时滞效应的股票期权定价与原保险费率等都可以用以下时滞倒向随机微分方程进行刻画.

(3.1)

其中,μ(t)表示资产在t时刻的回报率,σ(t)表示在t时刻的波动率.

方程(3.1)为线性的时滞倒向随机微分方程,方程生成元包含当前t时刻和过去t-δ时刻解的值.可见方程(3.1)为方程(1.1)的特殊形式,由定理2.1可知其存在唯一解.

下面介绍与之对偶的超前随机微分方程:

(3.2)

定理3.1 时滞倒向随机微分方程(3.1)的解Y•可由以下闭式给出:

其中,X(s)是以下超前随机微分方程的解:

(3.3)

证明 首先证明(3.3)有唯一解.当s∈[T-δ,T]时,(3.3)变为

(3.4)

易知(3.4)有唯一解λ•.当s∈[t,T]时,(3.3)变为

(3.5)

可见方程(3.5)是一个经典的超前随机微分方程,由定理2.2可知,方程(3.5)存在唯一解.

对X(s)Y(s)在s∈[t,T]上应用It’s公式,

等式两边取条件期望,

由于X(t)=1,X(t)=0,s∈[T,T+δ],则有

综上所述,本文通过时滞倒向随机微分方程与超前随机微分方程之间的对偶性,将超前随机微分方程作为伴随过程,得出了解的最优控制,在具有延迟盈余的养老金动态最优、具有时滞效应的股票期权定价与原保险费率等前提下,可利用该最优控制方法解决金融产品定价问题.