t-extending模的直和
李煜彦,何东林
(陇南师范高等专科学校数学与信息科学学院,甘肃 陇南 742500)
模及其相关问题受到许多作者的关注[1-8]。称M是extending模,如果M的每个闭子模是M的直和因子。2011年,Asgari和Haghany[9]引入了t-extending模的概念,它是extending模的一个推广,文中研究了t-extending模的性质及等价刻画。随后2013至2019年期间,Asgari等人[10-13]在t-extending模的基础上又相继研究了t-半单模,t-连续模和t-拟连续模,讨论了这些模类的性质,分别给出了它们的等价刻画。特别地,作者证明了M是t-extending模(t-半单模,t-连续模,t-拟连续模)当且仅当M=Z2(M)⊕M′,其中M′是非奇异的extending模(半单模,连续模,拟连续模)。受此启发,本文提出了t-补子模的概念,研究了t-extending模的直和分解,证明了M=⊕i∈IMi(|I|≥2)是t-extending模的两个等价条件。
1 预备知识
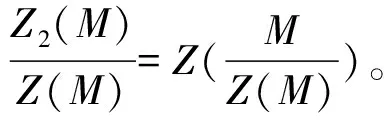
下面给出本文所用到的一些基本结论。
引理1[9]以下对模M等价:
1)M是t-extending模;

3)M=Z2(M)⊕M′,其中M′是(非奇异) extending模;
4)M的包含Z2(M)的任意子模是其直和因子的本质子模;
5)对任意N≤M,存在M的直和因子K,使得N≤tesK;

引理2[10]M的任意子模都存在t-闭包。
2 主要结果
定义1设K,N≤M,称K是N在M中的t-补,如果K是{L≤M|L∩N≤Z2(M)}中的极大元。称A是M的t-补子模,如果存在B≤M,使得A是B在M中的t-补。
由[9],[10]和引理2易得如下结论。
推论1C是M的t-闭子模当且仅当C是M的t-补子模。
推论2M的任意子模都存在t-补。
推论3若M是非奇异模,则
1)C是M的t-本质子模当且仅当C是M的本质子模;
2)C是M的t-补子模当且仅当C是M的补子模。
下面例子说明t-闭子模是闭子模,但反之未必。从而由推论1知,t-补子模是补子模,但反之未必。
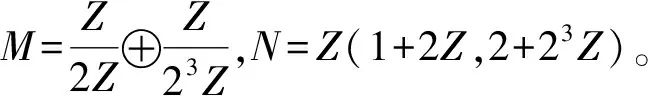
由于内射模是extending模,故内射模是t-extending模。下面讨论t-extending模的直和因子的内射性。
性质1设M=M1⊕M2,且M是满足(C3)条件的t-extending模。若M1是非奇异的,则M1是M2-内射的。
证明对任意N≤M2以及任意R-同态映射f:N→M1。令W={x-f(x)|x∈N},则W≤M,且W∩M1=0。由Zorn’s引理,存在M1在M中的t-补L,使得W⊆L,且L∩M1≤Z2(M)。由于M1是非奇异的,故L∩M1是Z2-挠且非奇异的,从而L∩M1=0。由M是t-extending模可知,L是M的直和因子。又M满足(C3)条件,于是L⊕M1是M的直和因子。设存在H≤M,使得M=(L⊕M1)⊕H=M1⊕(L⊕H)。令π:M→M1是自然投射,则W⊆Kerπ=L⊕H。于是对任意x∈N,易知下面等式成立:π(x)=π(x-f(x)+f(x))=π(f(x))=f(x)。
从而有如下交换图:
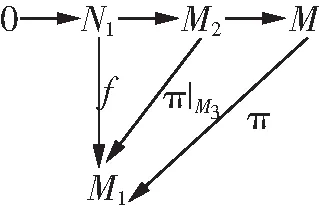
图1 交换图F
即π|M2是f的扩张,所以M1是M2-内射的。
由性质1,易得下面结论。
推论4若M是满足(C3)条件的t-extending模。则存在M的直和因子N,使得M=Z2(M)⊕N,且N是Z2(M)-内射的。
证明因为M是t-extending模,由引理1知,存在M的直和因子N,使得M=Z2(M)⊕N,其中N是非奇异的extending模。于是由性质1知,N是Z2(M)-内射的。
下面例子将说明t-extending模的直和未必仍是t-extending模。
例2设R=Z[x]。由[9]知,RR是extending模,但(R⊕R)R不是extending模。由于R是右非奇异的,故RR是t-extending模,但(R⊕R)R不是t-extending模。
一个自然地问题是,什么情况下t-extending模的直和扔是t-extending的?下面先给出两个模的直和是t-extending模的充分条件。
性质2设M=M1⊕M2。若M1是非奇异的t-extending模,M2是Z2-挠的,则M是t-extending模。
证明设N≤tcM,由[9]引理2.5知,Z2(M)=Z2(M1⊕M2)≤N。因为M1是非奇异的,M2是Z2-挠的,所以Z2(N)=Z2(M)=Z2(M1)⊕Z2(M2)=M2,从而
N=N∩(M1⊕M2)=N∩(M1⊕Z2(N))=
Z2(N)⊕(N∩M1)=M2⊕(N∩M1)
设L≤M1且N∩M1≤tesL,由[10]推论1.2知,N=M2⊕(N∩M1)≤tesM2⊕L。因为N≤tcM,所以N=M2⊕(N∩M1)=M2⊕L。从而N∩M1=L,即N∩M1是M1的t-闭子模,因此N∩M1是M1的直和因子。设H≤M1,使得M1=H⊕(N∩M1),则M=H⊕(N∩M1)⊕M2=H⊕N。即N是M的直和因子,从而M是t-extending模。
事实上,性质2中的条件“M1是非奇异的”是可以去掉的。于是有下面结论。
推论5设M=M1⊕M2。若M1是t-extending模,M2是Z2-挠的,则M是t-extending模。
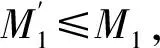
综上所述,M是t-extending模。
引理3[15]设M=M1⊕M2,其中Mi(i=1,2)是extending模。则M是extending模当且仅当对M的任意闭子模K,若K∩M1=0或K∩M2=0,则K是M的直和因子。
下面考虑t-extending模保持直和的问题。
定理1设M=M1⊕M2,其中Mi是t-extending模,且Mi=Z2(Mi)⊕Ni(i=1,2)。则M是t-extending模当且仅当对任意K≤tcN1⊕N2,若K∩N1=0或K∩N2=0,则K是M的直和因子。
证明必要性,设M是t-extending模,K≤tcN1⊕N2。则M=M1⊕M2=(Z2(M1)⊕N1)⊕(Z2(M2)⊕N2)=Z2(M1⊕M2)⊕(N1⊕N2),由[9]知,N1⊕N2是t-extending模,所以K是N1⊕N2的直和因子。从而K是M的直和因子。
充分性,设对任意K≤tcN1⊕N2,若K∩N1=0或K∩N2=0,则K是M的直和因子。由于Mi(i=1,2)是t-extending模,由引理1(3)知,N1和N2都是extending模。又因为K是N1⊕N2的闭子模,所以由引理3知,N1⊕N2是extending模,因此N1⊕N2是t-extending模。由于M=Z2(M1⊕M2)⊕(N1⊕N2),由推论5知,M是t-extending模。
定理2设M=⊕i∈IMi(|I|≥2)。则以下等价
1)M是t-extending模;
2)存在i≠j∈I,使得对M的任意t-闭子模K,若K∩Mi≤Z2(M)或K∩Mj≤Z2(M),则K是M的直和因子;
3)存在i≠j∈I,使得Mj或Mi在M中的任意t-补是t-extending模且是M的直和因子。
证明(1)⟹(2)显然成立。
(2)⟹(3)设K是Mi在M中的t-补,则K∩Mi≤Z2(M)。由(2)知,K是M的直和因子。设L≤tcK,由[9]知,L≤tcM。而L∩Mi⊆K∩Mi≤Z2(M),由(2)知,L是M的直和因子,故也是K的直和因子。从而K是t-extending模。
(3)⟹(1)设N≤tcM,引理2知,存在L≤N,使得L是N∩Mi在N中的t-闭包。于是0=(N∩Mi)∩Mj≤tesL∩Mj,L∩Mj≤Z2(L)≤Z2(M)。由推论2,存在Mj在M中的t-补E,使得L⊆E。由(3)知,E是t-extending模且是M的直和因子。易知L≤tcM,由[9]性质2.8知,L≤tcE。所以L是E的直和因子,从而L是M的直和因子。设存在L′≤M,使得M=L⊕L′,则N=L⊕(N∩L′)。于是存在K≤N,使得K是N∩L′在N中的t-闭包。易知K∩L≤Z2(K)≤Z2(M),且K=K∩N=(K∩L)⊕(N∩L′)。下证K∩Mi≤Z2(M),从而可得K是Mi在M中的t-补。设m∈K∩Mi,则m=a+b,其中a∈K∩L,b∈N∩L′。因为K∩L≤Z2(M),所以存在I≤tesR,使得aI=0。于是mI=bI∈(N∩L′)∩Mi=0。从而b∈Z2(N∩L′)=0,即m=a∈Z2(M)。由(3)知,K=(K∩L)⊕(N∩L′)是M的直和因子,故N∩L′是M的直和因子。从而N=L⊕(N∩L′)是M的直和因子。
定理3设M=M1⊕M2,其中Mi是t-extending模,且Mi=Z2(Mi)⊕Ni(i=1,2)。若以下两条分别成立,则M是t-extending模。
1)Ni(i=1,2)是相互内射的;
2)对任意L1≤N1,L2≤N2,都Hom(L1,N2)=0和Hom(N1,L2)=0。
证明1)设Ni(i=1,2)是相互内射的。由于M=Z2(M1⊕M2)⊕(N1⊕N2),由推论5知,只需证N1⊕N2是t-extending模。设K≤tcN1⊕N2,且K∩N1=0。由[15]引理7.5知,存在L≤N1⊕N2,使得N1⊕N2=N1⊕L,且K⊆L,故N2≅L。由[9]性质2.14知,N1和N2都是t-extending模,从而L是t-extending模。于是由[9]推论2.8知,K是L的直和因子,从而K是N1⊕N2的直和因子。即N1⊕N2是t-extending模。类似地,若K≤tcN1⊕N2,且K∩N2=0,则N1⊕N2是t-extending模。
2)设K≤tcM,且K∩M1≤Z2(M)。由[9]知,Z2(M)≤K。于是Z2(M1)⊆M1∩K⊆M1∩Z2(M)=Z2(M1),因此Z2(M1)=M1∩K。从而N1∩K=N1∩Z2(M1)=0。于是K=K∩(Z2(M)⊕(N1⊕N2))=Z2(M)⊕(K∩(N1⊕N2))=Z2(M)⊕W,其中W=K∩(N1⊕N2)。由于K≤tcM,由[9]性质2.9可得,W=K∩(N1⊕N2)≤tcN1⊕N2。令πi:N1⊕N2→Ni(i=1,2)是标准投射,则Ker(π2|W)=(Kerπ2)∩W=N1∩W=N1∩K=0。故π2|W:W→N2是单同态。因为π1|W=π1(π2|W):π2(W)→N1,由假设Hom(π2(W),N1)=0,所以π1(W)=0,因此W⊆Kerπ1=N2。由引理1知,N2是extending模,故W是N2的直和因子,因此W是M的直和因子。从而K=Z2(M)⊕W是M的直和因子。由定理2知,M是t-extending模。

