关于Chidume-Zegeye-Ntatin定理的注释
李小玲,曹寒问
(南昌工程学院理学院,江西 南昌 330099)
1967年Browder[1]和Kato[2]分别独立提出了增生映射及与之有关的伪压缩映射。增生映射早期的基本结果是Browder研究的初值问题
其中,A是增生且局部Lipschitz的。因增生映射在工程和物理中大量存在,自提出时起,该问题就引起许多学者的广泛关注,见[3-8]
定义1.1映射A:D(A)⊆X→X称为增生的。如果对∀x,y∈D(A),存在j(x-y)∈J(x-y),使得
〈Ax-Ay,j(x-y)〉≥0
(1)
定义1.2映射A:D(A)⊆X→X称为强增生的。如果对∀x,y∈D(A),存在j(x-y)∈J(x-y)及一实数k>0,使得
〈Ax-Ay,j(x-y)〉≥k‖x-y‖2
(2)
定义1.3映射A:D(A)⊆X→X称为φ-强增生的。如果对∀x,y∈D(A),存在j(x-y)∈J(x-y)及一严格递增函数φ:R+→R+且φ(0)=0,使得
〈Ax-Ay,j(x-y)〉≥
φ(‖x-y‖)‖x-y‖
(3)
定义1.4映射A增生且对∀λ>0,(I+λE)D(A)=X,则称A为m-增生,其中I为单位映射。
比较早期的迭代程序是由Mann[9]及Ishikawa[10]提出的.对于非线性强增生映射,Liu[11]在1995年提出了带误差的Mann迭代和带误差的Ishikawa迭代,迭代如下:
设X是实Banach空间,K是X的非空子集,T:K→X,x0∈K,序列{xn}定义为:
xn+1=(1-αn)xn+αnTyn+un
yn=(1-βn)xn+βnTxn+vn,n≥0
(a)
其中:{αn},{βn}⊆(0,1);∑‖un‖<∞,∑‖vn‖<∞,称(a)为带误差的Ishikawa迭代。
在(a)式中序列{xn}定义为:
xn+1=(1-αn)xn+αnTxn+un,n≥0
(b)
其它T,K,X,{αn},{un}同(a)式,称(b)式为带误差的Mann迭代。对于Liu提出的带误差的Mann迭代和Ishikawa迭代,由于∑‖un‖<∞,∑‖vn‖<∞,从而误差项一定要求趋于零。1998年,Xu[12]使用了下列形式的带误差的Ishikawa和Mann迭代。
设X是实Banach空间,K是X的非空凸子集,T:K→K,x0∈K,序列{xn}定义为:
xn+1=anxn+bnTyn+cnun,
(c)
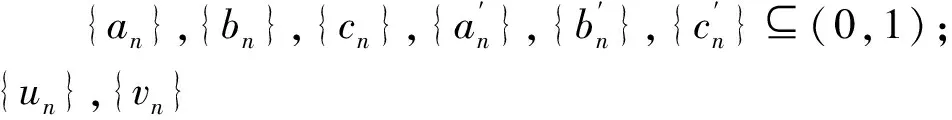
称(c)为带误差的Ishikawa迭代。
在(c)式中序列{xn}定义为:
xn+1=anxn+bnTxn+cnun,n≥0
(d)
关于增生类映射及伪压缩类映射在带误差的迭代序列方面的研究非常丰富,见[13-15]。本文研究的是Xu提出的带误差的Ishikawa迭代。
1 预备知识
设X为一实Banach空间,‖·‖与X*分别为范数和对偶空间,正规对偶映射J:X→2X*定义如下:
J(x)={f∈X*:〈x,f〉=
‖x‖‖f‖,‖x‖=‖f‖},∀x∈X
其中〈.,.〉为其对偶对。若X*为严格凸,则J是单值的;若X*为一致凸,则J在X的有界子集上一致连续。
引理2.1[16]设X为实Banach空间,J是正规对偶映射,对∀j(x-y)∈J(x-y),有
‖x+y‖2≤‖x‖2+
2〈y,j(x+y)〉,∀x,y∈X
条件(Ⅰ)增生映射A称为满足条件(Ⅰ),若对N(A)={x|Ax=0,x∈D(A)}≠∅,∀x∈D(A),∀p∈N(A),∀j(x-p)∈J(x-p),有〈Ax,j(x-p)〉=0成立当且仅当Ax=Ap=0。
Chidume,Zegeye及Ntatin在[3]中研究了下列最速下降逼近程序的收敛性:
xn+1=Qpn
pn=anxn+bn(I-A)yn+cnun
(4)
其中Q:X→clD(A)称为非扩张保核收缩的。在[3]中证明了下述定理。
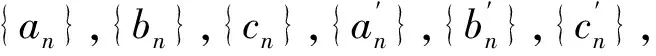

〈Ayn-Ax*,j(yn-x*)〉≥
φ(‖yn-x*‖)‖yn-x*‖
(5)
对于上述,我们指出三点:
(a) 该定理的结论是正确的;
(b) 该定理的证明过程过于冗长(P54-P63);
(c) 关于{xn}有界的证明不完全。在{xn}有界的证明中,文[3]是这样证明的:“若‖xn0+1-x*‖>a0,则由前面的结论,我们有‖xn0+2-x*‖≤‖xn0+1-x*‖”(见[3]中P59第20行)。但是前面的结论是“若‖xn0-x*‖>a0,‖xn0-1-x*‖≤a0,则‖xn0+1-x*‖≤‖xn0-x*‖”(见[3]中P57-P59)。因此,若我们仅有‖xn0+1-x*‖>a0,而没有‖xn0-1-x*‖≤a0,那么就不知道不等式‖xn0+2-x*‖≤‖xn0+1-x*‖是否成立。
因此,我们在本文对定理CZN给出一种新且比较简短的证明。
2 定理CZN的证明

xn+1=Qpn
pn=xn-αnAyn-Un
(6)

必要性 必要性的证明同[3]中必要性证明。
充分性 第一种情况:对∀n≥0,Ayn=0时,与[3]中同样证明,可以得到{xn}收敛于x*∈D(A)且x*是唯一的。
第二种情况 若存在n,使得Ayn≠0。不失一般性,我们不妨假设Ay0≠0。由(6)及(5),我们可以得到‖y0-x*‖≤φ-1(‖Ay0‖)及
‖x0-x*‖≤‖x0-y0‖+‖y0-x*‖≤
‖x0‖+m+φ-1(‖Ay0‖)
(7)
其中m:=max{sup{‖vn‖},sup{‖un‖}},且设
a0=‖x0‖+m+φ-1(‖Ay0‖)
M(x0)=sup{‖Au‖:‖u-x0‖≤
4(a0+r(a0))},R(x0)=4{M(x0)+
r(a0)+m+a0+‖x0‖}
(8)

‖j(x)-j(y)‖<ε
设
(9)
第一步证明 若‖xn-x*‖ ‖yn-x*‖≤a0+2r(a0), ‖pn-x*‖≤a0+2r(a0) (10) 由(6),我们有 a0+r(a0) 通过(8)(9),可得到 ‖yn‖≤‖yn-x*‖+‖x0-x*‖+ ‖x0‖≤a0+r(a0)+a0+‖x0‖≤ 2a0+r(a0)+‖x0‖≤ 3a0+r(a0),‖Ayn‖≤M(x0) ‖Un‖= m)≤cn(4a0+3r(a0)+M(x0)+2m+ 因此 ‖pn-x*‖=‖xn-x*‖+ αn‖Ayn‖+‖Un‖≤a0+r(a0)+ αn(M(x0)+r(a0))≤a0+2r(a0) 从而第一步得证。 第二步证明 对∀n≥0,‖xn-x*‖≤a0。 下面用归纳法做证明。由(7)知,当n=0时,成立。假设为n时,有‖xn-x*‖≤a0。下面证明‖xn+1-x*‖≤a0。假设不成立,即‖xn+1-x*‖>a0。因‖xn-x*‖≤a0,故 ‖xn‖≤‖xn-x*‖+‖x*-x0‖+ ‖x0‖≤2a0+‖x0‖ 通过(10),(8),得到 ‖yn-x0‖≤‖yn-x*‖+‖x*-x0‖≤ a0+2r(a0)+a0≤2(a0+r(a0)) ‖Ayn‖≤M(x0) 由(5),(6)及[16]再结合上面关系式,我们有 ‖xn+1-x*‖2≤‖pn-x*‖2= ‖xn-x*-αnAyn-Un‖2≤‖xn-x*‖2- 2αn〈Ayn-Ax*,j(pn-x*)-j(yn-x*)〉- 2αn〈Ayn-Ax*,j(yn-x*)〉- 2〈Un,j(pn-x*)〉≤‖xn-x*‖2+ 2αnM(x0)‖j(pn-x*)-j(yn-x*)‖- 2αnφ(‖yn-x*‖)‖yn-x*‖+ 2‖Un‖‖pn-x*‖ (11) 注意到(6),条件(ⅱ)及(9) ‖yn-x*‖≥‖xn+1-x*‖-‖yn-xn+1‖≥ ‖xn+1-x*‖-‖yn-pn‖=‖xn+1-x*‖- ‖x0‖+m))≥a0-(αnM(x0)+r(a0)+2a0+ (12) 运用(8),(6),(9)及条件(ⅲ) ‖xn+1-x*‖2≤‖pn-x*‖2= ‖xn-x*-αnAyn-Un‖2≤ 由于pn-x*,yn-x*∈B(0,4(a0+r(a0))),结合X的有界子集上映射j一致连续,得到 (13) 将(12),(13)代入(11),有 a0<‖xn+1-x*‖2≤‖xn-x*‖2+ 矛盾。从而对∀n≥0,‖xn-x*‖≤a0,即{xn}有界。 第三步证明 {xn}收敛于x*∈D(A)。 因{xn},{yn},{pn}有界,结合已知条件,有 ‖xn+1-x*‖2≤‖xn-x*‖2- 2αn〈Ayn-Ax*,j(pn-x*)-j(yn-x*)〉- 2αn〈Ayn-Ax*,j(yn-x*)〉-2〈Un,j(pn- x*)〉≤‖xn-x*‖2-2αn〈Ayn-Ax*,j(yn- x*)〉+o(αn) (14) φ(‖yn-x*‖)‖yn-x*‖> (15) 又存在整数 (16) 因此,通过(15),(16),对∀n≥N1,由(14)可得 由上式,有 ‖xnj-x*‖<ε 类似{xn}有界性的证明,我们可以证明到‖xnj+m-x*‖<ε,∀m≥1。即n→∞时,xn→x*。该定理的充分性证完。 本文主要是对Chidume,Zegeye,Ntatin中的定理1进行探讨,首先是通过新的方法证明了迭代序列{xn}的有界性;然后是通过一种比较简短的方式对定理1进行了证明;由于同样的方法可以证明文献[3]中的定理2,所以本文推广和改进了相关结果。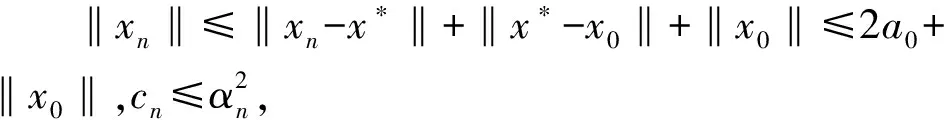


3 结论

