集映射、拓扑交和对影序的存在性

卢美华,高晓波

(1.江西科技学院理科部,江西 南昌 330022;2.江西农业大学计算机与信息工程学院,江西 南昌 330045)

序拓扑理论是当前应用拓扑发展的重要方向,诸多新方法、新思维已经应用于并更新了序拓扑空间、广义度量空间的理论局面。序拓扑空间及其在经济领域的应用获得了国家自然科学基金群聚焦式资助。稍早,师维学在三个国家自然科学项目形成项目群的资助下,解决了序拓扑空间上广义度量的构造等诸多问题,当然,标度序族的集结不在其自然科学基金群的研究之中[1]。虽然标准形式理性一般能严格效用函数化,有限理性也可效用扰动化[2],但序拓扑却更方便刻画理性的有限性、不完全性等,特别是集体理性、群理性等等。众所周知,“共识”作为标度序族的某种一致性也受到广泛研究,群决策共识和一致性同样受到国家自然科学基金群的资助下,但从其概念体系到约束体系公理化的研究却十分不足[3]。即使对各种不同类型序(各种偏好关系),虽然都可以建立迭代算法以确定“共识”,但迭代算法中个体理性、群体理性难以相容,迭代算法破坏着个体理性。文献[3]总结的系列研究结论,发现符合一般研究范式的“共识理论”应该统一“交互共识”和“优化共识”,本质上通向社会选择理论,并为社会选择理论和共识协商形成了概念连接。

事实上,社会选择理论一直是公理化群序及其集结形式化理论的典范。当前,几何社会选择理论和拓扑社会选择理论确实拓宽了社会选择理论的进路[4],但是约束公理相容性配置却一直处于争执之中[5]。如果分析文献[3]总结的系列方法,可以发现集结落实到单纯算法层面上,则约束公理配置确实是内化到运算之中,从而其一般研究范式具有统一性,但也产生了算法统一性问题。本文力求仅在运算层面上实现概念刻画和集结特征判断,并集中考察社会选择函数集结中的对影判别和性质;一方面,以交运算统一刻画和描述,形成算法统一性。另一方面,进行序性严格化,消除群序集结中形式混乱。其结论可以证明弱序集结空间和强序集结空间构造的等价性,其中的关键在于对影分解和结合,理清对影的性质,并合理的判别对影。

1 知识准备和符号说明

在文献[6]提出了强序新的刻画。而近期卢进一步提出集序、群序,并基于集序、群序刻画了偏好集结,获得了诸多良好得结论[7]。其方法体系是用集值映射刻画序,在集值映射上装载各约束形式并对应地刻画出强序、弱序、全序、偏序,乃至锥序;在集序构造下发现群序集结可等价于群强序集结。同时,高、卢在文献[8]提出对影概念,并研究了对影判别和性质。而且,卢文献[7]把集序、群序集结应用于社会选择理论得基础构造。这里基础构造理论联系广阔,诺贝尔经济学奖获得者马斯金在机制研究中,从连续统空间得测度等分构造选择主体,以此构造考察约束公理得强弱,并给出一个约束公理系统得包含关系[9]。一旦采用卢提出得集序、群序方法,约束公理得加载将更为便利。本质上,卢的方法体系是避免约束公理加载而前置在运算层面上考察一般集结性质,这避免了后置约束公理不相容性的缺陷,例如Arrow不可能性。在基本集结性质清晰后,加载约束公理的强弱性就能自明。为此,下面给出基本概念。

关系及其属性是形式决策理论的起点。给定X集合,以范数|X|表示集合元素个数。设R⊂X×X,以该子集R表示集合X上元素的关系,若(x,y)∈R,称x关系R于y,此时也可记为xRy。同时,装载了关系后集合记为(X,R)。对于(X,R),称R为自反性关系,若任何x都有xRx。对应地,若任何x都有┒xRx(表示xRx不成立),则可称R为非自反性关系。称R为传递性关系,若任何x,y,z,由xRy及yRz能推出xRz。称R为对称性关系,对任何不同的x、y,xRy能推出yRx;称R为反对称性关系,对任何不同的x、y,xRy能推出yRx;称R为完全性关系,若对任何不同的x、y,xRy能推出┒yRx。另外,基于关系属性可定义特定关系,例如(X,R)为弱序集,若关系R是自反性、传递性关系;而后续主要采用集值映射定义各类关系。

定义1设集合X上集值映射F:X→2X满足(1)∀a∈X,a∈F(a);(2)∀b∈F(a)有F(b)⊂F(a);(3)若┑a∈F(b)则b∈F(a);则称F:S→2S为集序映射,简称为集序,同时记X为(X,F)。

显然,依据集序把b∈F(a)记为关系ba,则“”是传递性关系。另外由“b∈F(a)”推导出“F(b)⊂F(a)”刻画了集序映射收缩性,该映射收缩性与关系传递性互为判断,并且映射收缩性刻画“优向”判断;反之,映射刻画集序的扩张性能为关系“劣向”提供判断。对于(X,F)的X中任何α∈X,记F-1(α)={β|α∈F(β)},映射是扩张的,称为逆象集。

另外,仍可依据集序来刻画关系对称性、关系完全性。例如,称集序F是对称的,如果对任何两个a、b∈X,a∈F(b)能推出b∈F(a);反对称性即a∈F(b)能推出┑b∈F(a)。称集序F是完全的,对任何两个a、b∈X,┑a∈F(b)能导出b∈F(a);集序属性显然是自明的。同时,以FX表示X上全体集序形成的集合,称FX为X的集序空间,简称集序空间。显然,FX={F:X→2X|F满足a∈F(a),[∀b∈F(a)]⟹F(b)⊂F(a)}。

为形式化地综合考虑社会选择理论、机制设计理论,需要准确定义文献[9]所指称的集结,即把一个标度集下的偏好组合映射为社会偏好。为方便直接记V={1,2,…m}直接表示标度集,并定义社会选择函数如下:

定义2标度集V对集合X建立了集序组合形成组合空间FXV={(F1,F2,…Fm)|Fi∈FX}。即FXV=FX×FX×…×FX为m个FX形成笛卡尔积,并称FXV为标度集V标度集序空间,简称为标度集序空间。在(V,FX)的标度集序空间FXV中,称SCF:FXV→FX为V标度集下X的群序集结,简称群序集结。

文献[7]采用循环群在等价族上定序,而当采用拓扑运算定序将和和集结具有一致性。为此,本文再提出单元收缩映射保证在等价族上一致性定序。

定义3称T:2X→2X为单元收缩映射,若T满足∀Λ∈2X有T(Λ)⊂Λ及|Λ|-|T(Λ)|=1。对于一单元收缩映射T,称T循环收缩直至形成空集终止而形成的套链T(X)、T(T(X))、…、T(…T(X))为T的承接链;同时,称T对A∈2X循环收缩直至形成空集终止而形成的套链T(A)、T(T(A))、…、T(…T(A))为(T,A)承接链,在自明情形下可简称承接链。

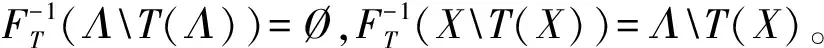
2 主要结论

一般地,考察偏好集结的社会选择函数框架为(X,V,FXV,FX),但偏好严格化涉及对影集结,从而扩充框架为(X,V,FXV,FX,T)。另外,SCF:FXV→FX中偏好集结需要遵循约束公理,并且,阿罗、森、马斯金在其诺贝尔获奖成果中都配置过不同的约束公理系统;为此,既然不研究约束公理的配置合理性,本文仅依据马斯金在文献[8]的配置模式记一般性约束公理系统为AS,在考虑集结过程中充分回避配置约束公理仅采用基础运算进行形成刻画,将主要形成以下定理。其中,需要运用逆象、单元收缩等运算。

定理1在(X,F)中作F0(α)=F(α)∩F-1(α),则{F0(α)|α∈X}重合合并后能形成X的一个分划,即X=∪α∈XF0(α),其中并元F0(α)、F0(β)或者交空,或者相等。

证明(X,F)中集序F是自反和传递的,则∀α∈X都有α∈F(α),从而有α∈F-1(α)。综合则有α∈F(α)∩F-1(α),也即α∈F0(α),则任何F0(α)都非空;由以上α的任意性,必有X⊂∪α∈XF0(α),那么必然是X=∪α∈XF0(α)。余下要证明{F0(α)|α∈X}能形成X的一个分划,其关键在于证明任何两个有差异的F0(α)交空。

∀α、β∈X考察F0(α)、F0(β)。情形一,若F0(α)∩F0(β)=∅,即两者已交空。情形二,若F0(α)∩F0(β)≠∅,则需证明F0(α)=F0(β),即F0(α)、F0(β)有没有差异。

为此,设F0(α)∩F0(β)≠∅,则可取定c∈F0(α)∩F0(β)并考虑两个方面。一方面,对任意一个η∈F0(α),可证明必然有η∈F0(β)。由于c∈F0(α)及η∈F0(α)可以展开为c∈F(α)、α∈F(c)、η∈F(β)、α∈F(η),那么可以形成不同组合。由组合α∈F(c)、η∈F(α)并利用集序收缩性必然有η∈F(c);而再由c∈F(α)、α∈F(η)同样利用集序收缩性可得到c∈F(α)⊂F(η)即c∈F(η)。另一方面,由η∈F(c)、c∈F(η)及c∈F(β)、β∈F(c)也可以构造不同组合并运用集序收缩性,则有η∈F(c)、c∈F(β)⟹η∈F(β);c∈F(η)、β∈F(c)⟹β∈F(η)。这就有η∈F(β)、β∈F(η),也就是有η∈F(β)、η∈F-1(β),即η∈F(β)∩F-1(β),从而证明了η∈F0(β)成立。于是必然有F0(α)⊂F0(β)成立。考虑到证明过程的对称性,同样的道理必有F0(β)⊂F0(α)。结合已证结论,全面综合后必然有F0(α)=F0(β)成立。

综合以上整个证明,显然定理1成立。

一般地,按文献称{F0(α)|α∈X}为(X,F)等价族划分。同时有文献证明{F0(α)|α∈X}形成划分可以用(∩γ∈Λ0F(γ))及各F-1(a)形成非空最小收缩方式达成。该定理中,F0(α)∩F0(β)≠∅能推导到F0(α)=F0(β),这和该文献中的非空最小收缩子的结论是一致的。另外,从集序空间FX与空间RX的等价性上,后续研究仅仅只需在集序空间FX上进行即可。进一步,考虑集序空间FX形成划分的集序特征,任何集序F对X的划分只能是两种情形,即从F0(α)来看,或者F0(α)={α}为单点集,或者F0(α)={α、…、β}为非单点集。在单点集F0(α)={α},文献[8]对影是简单的,其对影集结困难性源于非单点集F0(α)={α、…β}。同时,文献[8]正是依据对影集结发现了社会选择函数面临孔多塞循环时可能导致集结不可能性,这一情形揭示了孔多塞循环和轮换循环之间存在本质联系;孔多塞循环就是多次轮换的推广。文献[8]在构造对影φαβR=时,其要点在于A/～={Λ1、Λ2、…、Λk}的商空间上分析A=Λ1∪Λ2∪…∪Λk的构成,在非单点的Λ上才需要对影构造。而一旦严格以运算进攻相关刻画,在(X,F)上作{F0(α)|α∈X}划分,并不需要繁复地定义对影,而直接运算出对影来。

下面依据文献[8]给出对影偏好的定义,对(X,F)采用集序刻画划分对{F0(α)|α∈X}中非单点集F0(α)中任何两点α、β的对影如下:称集序对为F在两点α、β上的有序对影集序,简称对影,记为φαβF=,并分别称F+、F-为左右分影,若F+、F-满足:(1)任何γ、η若F0(γ)∩F0(η)=∅,若γ∈F(η)(此时必有η∉F(γ))则对F+、F-分别规定,γ∈F+(η)、η∉F+(γ)以及γ∈F-(η)、η∉F-(γ);(2)任何γ、η若F0(γ)∩F0(η)≠∅,且F0(γ)∩F0(α)=∅,则对F+、F-分别规定,γ∈F+(η)、η∈F+(γ)及γ∈F-(η)、η∈F-(γ);(3)任何γ、η若F0(γ)∩F0(η)≠∅,且F0(γ)∩F0(α)≠∅。由于F0(γ)=F0(η)=F0(α)=F0(β)且γ、η、α、β∈F0(α),此时对F+、F-两方面分别规定:一方面,β∈F+(α)、α∉F+(β),其他任何不同于α、β的γ∈F0(α),β∈F+(γ)、γ∈F+(β);另一方面,α∈F-(β)、β∉F-(α),其他任何不同于α、β的γ∈F0(α),β∈F-(γ)、γ∈F-(β)。

以上定义φαβF=是基于集序F决定的分划中一个具体分划集中确定的两个等价元而形成的对影;当然,其中选择的两个等价元α、β具有自由度,并且后续将看到按对影定义取定的等价元α是实质性的,本质上φαβF可记为φαF。另外,其中获得的对影中两个分影都为集值映射,而且F+∈FX、F-∈FX,即F+、F-也在集序空间之中。由F+∈FX,也可再选定集序F+决定的分划中一个具体分划集中任意确定的两个等价元而形成的对影,具有左右分影;这里任意等价元确定后,由F-∈FX,集序F-决定的分划和F+决定的分划是相同的分划,F-依据已经确定了两个等价元也可形成的对影,具有左右分影。显然,F+的左分影和F-的右分影能形成对影,这在文献[8]中已经证明。累次把对影的左右分影做对影分解,左分影的下次左分影和右分影的下次右分影未必能形成对影,但是左右分影决定的划分是相同的,只要以相同的确定等价元作下次的左右分影,下次左分影和下次右分影能构造出对影。为此,文献[8]提出了整个F的对影φ(F)。显然,整个F的对影φ(F)在F决定的分划中具有自由度,从而造成构造路径的分歧。

显然,以轮换映射来构造偏好序的对影,十分繁复,但以一个具体的T:2X→2X单元收缩映射来构造整个F的对影φ(F),其中等价元的选择也具有自由度,表现为T:2X→2X单元收缩映射的自由性。但是,只要T:2X→2X单元收缩映射前置性确定了,整个F的对影φ(F)是确定的。为此,采用单元收缩映射构造和刻画对影是确定的并且非常简单。为方便论证,先给出单元收缩映射的一个引理。

引理在(X,F)上以{F0(α)|α∈X}形成X的分划上取Λ∈{F0(α)|α∈X}。若Λ为非单点集,不妨设β、γ∈Λ,并作F在两点β、γ上的有序对影集序φβγF=,则{{F0(α)|α∈X}Λ}∪{β}∪{Λβ}同时为两个集序(X,F+)等价族划分和(X,F-)等价族分划。而Λ为非单点集记T(Λ)=Λ{β},Λ为单点集,记T(Λ)=Ø,则可扩出某个单元收缩映射T:2X→2X。

该引理无需证明。按照文献[8],以及本文对影形成集序刻画,引理是自明的。而采用R及″″等符号定义对影必须依据两元刻画并记φαβFφβγF,但从{{F0(α)|α∈X}Λ}∪{β}∪{Λβ}来看φβγF可记为φβF,后续集序方法构造更为便利,为此采用单元对影也更准确,从而采用之。同时,这个引理说明:一个对影中的左右分影形成的等价族分划是相同的,一个对影还精细化了和细化了等价族分划。对影的逐步分影分解正对应着等价族分划的细分过程。如果,考虑单元收缩映射和等价族分划,显然不同的单元收缩映射可能在对影分解为左右分影中产生相同的收缩效果。这说明单元收缩映射的构造比对影分解构造更为广泛。

在(X,F)上加载某单元收缩映射T:2X→2X,取Λ∈{F0(α)|α∈X}为X分划的一个等价族,记supΛ=F(ΛT(Λ))F0(ΛT(Λ),并记F+:X→2X和F-:X→2X如下:

(1)

(2)

定理2在(X,F)上加载某个单元收缩映射T:2X→2X,在Λ∈{F0(α)|α∈X}取ΛT(Λ)=α,则由式(1)、式(2)决定的=φαF。式(1)、式(2)构造了F在点α上的有序对影集序。

证明按定理结论,需要证明式(1)、式(2)中集值映射是集序,并且构成的对影。本质上,明式(1)、式(2)的构造中实在F(x)收缩,即总有F+(x)⊂F(x)、F-(x)⊂F(x)成立。

先证明式(1)、式(2)中F+:X→2X、F-:X→2X为集序,即要整证F+、F-适合自反性、完全性和传递性。以F+为例试证,由于∀x∈X,x∈F(x),注意到式(1)中F+(x)三个部分,故而只需考虑x∈T(Λ)情形。再按定理2中标定的ΛT(Λ)=α,而又按单元收缩映射定义,T(Λ)=Λα,故x∈T(Λ)情形中x≠α,其F+(x)对应情形F(x){ΛT(Λ)}中仅排除ΛT(Λ),即仅排除α,而没有排除x。故x∈F(x)仍保证了x∈F(x){ΛT(Λ)}。故而,式(1)定义的F+(x)的三种情形都适应x∈F+(x),适合自反性。

再证式(1)定义的F+(x)适合传递性,即要证∀x∈X以及其中任何η∈F+(x),均有F+(η)⊂F+(x)。同样要注意式(1)中F+(x)三种情形,前两种情形中F+(x)=F(x),而式(1)中构造性总能保证F+(η)⊂F(η)成立,从而对于式(1)中F+(x)前两种情形x∉Λ或x=ΛT(Λ)=α中,总有F+(η)⊂F(η)⊂F(x)=F+(x)成立,即总有F+(η)⊂F+(x)。为此,只要证明式(1)中F+(x)为式(1)第三种x∈T(Λ)情形,F+(x)也适合传递性。此时F+(x)在F(x)上收缩了,但仅仅只收缩了单点,即F+(x)=F(x){ΛT(Λ)}=F(x)α。从而,考察x∈T(Λ)时的任何η∈F+(x)及对应F+(η),若F+(η)本身不含α(即α∉F+(η)),结合F+(η)⊂F(η)性质,总有F+(η)⊂F(η)⊂F(x),必然有F+(η)⊂F(x)α,那么F+(η)⊂F+(x)已经成立。

而当x∈T(Λ)及η∈F+(x)时,若F+(η)本身包含α(α∈F+(η)),那么由式(1)中F+(x)构造的第三情形中F(x){ΛT(Λ)}排除了α,所以此时F+(η)不在式(1)的F+(x)构造第二情形中,即η≠α(即ΛT(Λ));此时,只能是η∈T(Λ)或η∉Λ,对应记为第一种情况、第二种情况;并且后续将证明这里第二种情况将产生矛盾,从而只能是第一种情况。对于第一种情况η∈T(Λ),F+(η)=F(η){ΛT(Λ)}排除α,这就矛盾与F+(η)本身包含α。从而只能是第二种情况η∉Λ,而且x∈T(Λ)及η∈F+(x),α∈F+(η),这将导致矛盾。因为η∉Λ,Λ是在(X,F)等价族划分之中,既然ΛT(Λ)=α,α∈Λ,Λ=F0(α)=Λ=F(α)∩F-1(α),从而η∉F0(α)中是η∉F(α)或者η∉F-1(α),不过其中的“η∉F(α)”可以排除。为排除“η∉F(α)”,结合x∈T(Λ)及η∈F+(x),x∈T(Λ)⊂Λ=F0(α)保证了x∈F(α)且α∈F(x),而集序又保证了F(x)⊂F(α)且F(α)⊂F(x),则F(x)=F(α)。再由η∈F+(x)⊂F(x),结合F(x)=F(α),排除“η∉F(α)。从而η∉F0(α)中只能是η∉F-1(α)。

在第二种情况η∉Λ下,只能是η∉F-1(α),结合集序F的完全性,η∉F-1(α)推导出α∉F(η),那么F+(η)⊂F(η),那么α∉F+(η)这直接于在第二种情况的前提假设α∈F+(η)矛盾。于是,第二种情况并不出现。第一种情况F+已经适合了传递性。

综上所述,在F+的三种构造情形种,F+确实都是适合传递性的。下面证明F+适合完全性。为此,取任意的γ、η∈X,并设┑γ∈F+(η),只需要证明η∈F+(γ)。┑γ∈F+(η)按式(1)的F+三种构造,即第一种情形η∉Λ,F+(η)=F(η)时┑γ∈F+(η);第二种情形η=ΛT(Λ)=α,,F+(η)=F(η)时┑γ∈F+(η);第三种情形η∈T(Λ),,F+(η)=F(η){ΛT(Λ)}时┑γ∈F+(η)。

第一种情形η∉Λ,F+(η)=F(η)时┑γ∈F+(η),当然┑γ∈F(η),那么由F完全性,η∈F(γ);再由η∉Λ,η≠α,则η∈F(γ)α,从而无论F+(γ)处于式(1)的何种情况都有η∈F+(γ)。

第二种情形η=ΛT(Λ)=α,,F+(η)=F(η)时┑γ∈F+(η);当然┑γ∈F(η)(也即┑α∈F(η)),那么由F完全性有η∈F(γ)(也即α∈F(γ));按式(1)F+三种情形考察F+(γ),前两种情形在F+(γ)=F(γ),总有η∈F+(γ)成立。而一旦F+(γ)按第三种情形构造时,当然为γ∈T(Λ)(即γ∈Λ且γ≠α)F+(γ)=F(γ)α,但这将不会出现。因为此时,γ∈T(Λ)中虽然实质上γ∈Λ且γ≠α,但按照Λ等家族的属性,γ∈T(Λ)显然与┑γ∈F(η)本身矛盾;毕竟,γ∈T(Λ)保证了γ∈T(Λ)⊂Λ=F0(α)⊂F(α)=F(η)。

第三种情形η∈T(Λ),F+(η)=F(η){ΛT(Λ)}时┑γ∈F+(η)。这时,即使γ∈F(η)也会出现γ=α而导致┑γ∈F+(η),但这是仍然可证η∈F+(γ)。因为在γ=α时,η∈T(Λ)由Λ是等价族F0(α),这至少保证了η∈F(α),以及由η∈T(Λ)推出η≠α,从而η∈F(α)α,结合γ=α,当然有η∈F(γ)α,那至少在γ按式(1)第三情形也有η∈F+(γ)。

而第三种情形η∈T(Λ),F+(η)=F(η){ΛT(Λ)}时┑γ∈F+(η),即使γ≠α,也可证明η∈F+(γ)。显然,若γ≠α时┑γ∈F+(η)在即使其中F+(η)扩充α也成立,即┑γ∈(F+(η)∪{α})成立,则按式(1)构造,无论何种的T(γ)都会有┑γ∈F(η)成立。那么由集序F的完全性,┑γ∈F(η)保证了η∈F(γ),再结合η≠α,当然有η∈F(γ)α。于是按式(1)无论何种形式F+(γ)时,都有η∈F+(γ)。

合并以上三种情形的论证,都有┑γ∈F+(η)能导出η∈F+(γ),F+的完全性得证。

综上所述,F+是适合自反性、传递性、完全性,那么“F+是集序”成立。

如果比较式(1)的F+构造和式(2)的F-构造,F+与F-都是在F的特定点上压缩,F+是特定点上一次压缩,而F-是在特定点上多次压缩。一方面,从对称性上可以断定F-集序;另一方面,在α上逐次特定压缩F,按照以上证明都保证了每次压缩后的集序性,也可以断定F-集序。

余下即证明=φα(F)即可。依据文献[7]对影定义比较繁琐,而直接从对应的集序刻画的定义则极为方便。为此,证明=φα(F)只需以及对影集序特征,充分分析式(1)式(2)的构造即可,也即分三种情况分析即可。

按对影集序:(1)若任何γ、η满足F0(γ)∩F0(η)=∅,则显然γ、η不同时在Λ(即F0(α))之中。若γ、η都不在Λ中,按式(1)、式(2)规定的F+(γ)=F-(γ)=F(γ)以及F+(η)=F-(η)=F(η),显然由γ∈F(η)(此时必有η∉F(γ))能导出γ∈F+(η)、η∉F+(γ)以及γ∈F-(η)、η∉F-(γ)。而即使若γ、η只有一个在Λ中,以γ∈Λ而η∉Λ为例,按式(1)、式(2)规定的F+(η)=F-(η)=F(η),显然由γ∈F(η)(此时必有η∉F(γ))仍然能导出γ∈F+(η)、η∉F+(γ)以及γ∈F-(η)、η∉F-(γ)。

按对影集序:(2)若任何γ、η若F0(γ)∩F0(η)≠∅,且F0(γ)∩F0(α)=∅;此时必有F0(γ)=F0(η),F0(γ)∩F0(α)=∅,F0(η)∩F0(α)=∅,这将有γ、η都不在Λ中。按式(1)、式(2)规定的F+(γ)=F-(γ)=F(γ)以及F+(η)=F-(η)=F(η),结合F0(γ)=F0(η)直接就γ∈F+(η)、η∈F+(γ)以及γ∈F-(η)、η∈F-(γ)。

按对影集序:(3)若任何γ、η为不同元素,满足F0(γ)∩F0(η)≠∅且还满足F0(γ)∩F0(α)≠∅时,则F0(γ)=F0(η)=F0(α)且γ、η、α∈F0(α),F0(α)=Λ。此时,按式(1)、式(2)规定F+(γ)、F-(γ)可能会不等于F(γ),F+(η)、F-(η)可能会不等于F(η),需要分类判断式(1)、式(2)的F+、F-能否符合对影的集序特征。

此时,既然γ、η、α∈F0(α)=Λ,那么,可能γ、η≠α,或者γ、η仅一个为α。先考虑当γ、η≠α时,即γ、η∈T(Λ),按照式(1)、式(2)的构造,有F+(γ)=F(γ)α、F+(η)=F(η)α,而F-(γ)=F(γ)、F-(η)=F(η)。一方面,显然有γ、η∈F0(α)⊂F(α)=F+(α),但α∉F+(γ)=F(γ)α,α∉F+(η)=F(η)α,并且结合以前结论F(γ)=F(η)=F(α),并即使F(γ)、F(η)都排除α后得到F+(γ)、F+(η),但结合γ、η≠α,仍然有η∈F+(γ)、γ∈F+(η)成立。另一方面,由于有F-(γ)=F(γ)、F-(η)=F(η),同样结合以前结论F(γ)=F(η)=F(α),α∈F(α),并再次注意到F-(α)=F(α)T(Λ),从而有α∈F-(γ)、α∈F-(η)及γ、η∉F-(α),以及η∈F-(γ)、γ∈F-(η)同时成立。

再考虑γ、η仅一个为α,例如以γ≠α、η=α为例,但此时按“对影集序刻画”需要验证得“集序关系”事实上都在论证中得以验证了。从而,更符合“对影定义”。

从而式(1)、式(2)所规定得F+、F-确实适合对影定义”,=φαF。

全面综合以上所述,本定理得证。

定理3在(X,F)形成的集序空间FX上,对于任何一个集序F∈FX,均有F的对影φ(F)=存在。同时,对影φ(F)中并不唯一,可以以单元缩减构造。

说明,本定理是定理2的顺延,无需特别证明。只要把定理2中的单点对影构造φαF进行逐次循环构造即可,也即累次把对影的左右分影做对影分解,左分影的下次左分影和右分影的下次右分影未必能形成对影,但是左右分影决定的划分是相同的,只要以相同的确定等价元作下次的左右分影,下次左分影和下次右分影能构造出对影。

3 余论

上文考察了社会选择函数集结中的对影的构造和部分性质,其中对影中的左右分影能到序向的严格化。这就给出了弱序偏好的强序化路径,强序化为分影偏好,但集结中的一个弱序是等价于一组强序。上文通过分析对影的部分基本性质,在对影的判别中是可以联系孔多塞循环和轮换,但是,在对影构造上单元收缩映射更为普遍,在对影判别上轮换、等价族分解却更为方便。

另外,从文献[3]总结的系列方法,以及文献[12]的投影分析上,可以发现集结落实到单纯算法层面上,则约束公理配置确实是内化到运算之中,从而其一般研究范式具有统一性,但也产生了算法统一性问题。仅在运算层面上实现概念刻画和集结特征判断,显然能解决群决策中约束公理配置的混乱。例如,如果进一步完善偏好的严格化构造,则文献[14]所讨论的不完全偏好下的决策能完美解决了。基于以上拓扑构造的探索,后续进一步开拓共识的算法研究具有广阔的前景,文献[15]中的一些共识算法可再粗糙地构造,从而具有更普遍地适用性。