油孔数目对浮环轴承润滑静特性的影响*

康 洋 邱子桢 范其明 宋中越 师占群

(1.天津中德应用技术大学智能与制造学院 天津 300350；2.河北工业大学机械工程学院 天津 300130；3.中汽研新能源汽车检验中心(天津)有限公司 天津 300300；4.华中科技大学机械科学与工程学院 湖北武汉 430074)

浮环轴承具有内外双层油膜，被广泛应用于涡轮增压器、燃气轮机等高速轻载转子系统中[1]。与普通滑动轴承相比，浮环轴承具有相互耦合的特性，使得对其准确的理论研究存在一定的难度。因此，在当前浮环轴承具体的工程应用中，构建精准的理论模型主要是依赖于经验数据。

经典的流体动压滑动轴承动静特性的分析方法，是利用有限差分、有限元等离散数学方法求解Reynolds方程、Navier-Stokes方程或连续性方程，获得油膜压力场分布，再通过数值积分求得其他润滑动静特性参数[2-4]。然而，研究发现，无论是Reynolds边界条件还是JFO (Jakobsson，Floberg，Olsson)边界条件，都存在不足之处[5-6]。其中，Reynolds边界条件是在流体力学中使用的一种边界条件，它描述了流体在流动过程中的速度和压力分布情况。具体而言，Reynolds边界条件可以用来确定流体润滑膜的起始压力角度。然而，需要注意的是，Reynolds边界条件仅仅描述了流体的速度和压力分布，而并不能保证在边界处满足质量守恒条件，因而不适合于对滑动轴承端泄流量进一步分析。相比之下，JFO边界条件较好地解决了油膜在边界处的质量守恒条件，但其假设在油膜破裂开始与结束的位置压力不变。因此，JFO边界条件在处理高转速、大雷诺数的润滑工况时并不合理，而且具有数值计算相对复杂、迭代过程容易发散等缺点。

近年来，学者们将多相流理论引入到滑动轴承的润滑特性分析之中，其本质是将油膜区域视为一个整体，避免了人为设置边界条件所导致的误差，进而提高了计算结果的准确性。HU等[7]基于CFD (Computational Fluid Dynamics)方法对喷油润滑球轴承进行润滑特性分析，基于FLUENT软件中的VOF (Volume of Fluid)多相流模型求解润滑控制方程，讨论了在球轴承间隙中液态相和气态相之间的相变过程。此外，LIN等[8]发现对于同一轴承，在油气润滑下的承载能力高于纯油润滑下的承载能力，在油气润滑状态下轴承的散热性能优越。WU等[9]基于两相流理论研究了高速喷射冷却滚动轴承的的温度分布，发现轴承的温度分布受油体积分数分布的影响，较高的温度总是出现在较低的油体积分数区域；传统的油喷射润滑机制无法实现对高速滚珠轴承内圈的有效冷却。蒋红琰等[10]基于两相流理论，建立了含纳米气泡的两相流体动力润滑理论模型，利用有限差分法求解并得到了压力分布及水润滑轴承静、动态特性。李亚静等[11]通过采用两相流油膜破裂和非牛顿流体润滑油模型，研究了转速、偏心率、润滑油温度和润滑油压力等因素对油膜承载力和摩擦功耗的影响规律。

浮动环的转速在很大程度上影响着浮环轴承的润滑特性，目前一些学者在研究时将浮动环与轴颈转速之比简化为一固定的值[12]。然而，大量的实验结果表明，浮动环与轴颈转速之比在热效应的影响下并非恒定。针对这一现象，学者们做了相关的研究。其中，SAN ANDRÉS和KERTH[13]建立了热效应对浮环轴承动静特性参数影响的理论模型，并进行了实验验证。DYK等[14]通过对涡轮增压器动态特性分析，证实了浮环轴承的线性分析在对涡轮增压器转子动力学分析中可靠性。师占群等[15]建立了计入热效应影响的浮环轴承流体动压润滑模型，研究了考虑浮环受热发生变形的因素时供油温度对轴承静特性的影响。利用同一模型，裴世源等[16]研究发现热效应对浮环轴承的静动特性有显著的影响，指出浮环轴承的热膨胀效应将导致内外油膜间隙发生明显的变化。

本文作者根据先前所在团队对浮环轴承的润滑静特性的研究基础[17]，深入开展了在JFO边界条件下的浮环轴承的润滑静特性分析，具体讨论了浮环油孔数目对其润滑静特性参数的影响程度。首先，基于多相流理论建立浮环轴承的润滑模型，利用FLUENT求解器与其自定义函数接口对控制方程进行迭代求解。然后，将计算结果与文献[13]中的实验数据进行比对，验证理论模型的正确性。最后，将仿真范围扩展至宽域的润滑工况，研究浮动环圆周均布的油孔数目变化对浮环轴承摩擦功耗与内外油膜温升、固体元件温升、浮动环转速、端泄流量等润滑静特性参数变化规律的影响。

1 浮环轴承润滑理论模型的建立

图1和图2所示分别为浮环轴承的径向结构示意图和在Gambit软件环境下建立的有限元模型。为保证计算的稳定性和准确性，除轴瓦顶部与浮动环上的注油孔区域采用四面体网格之外，其余部分均划分为六面体结构化网格；浮动环的转动利用动网格与滑移边界相结合的方法来处理。

图1 浮环轴承的径向截面结构示意Fig.1 Schematic of the radial cross-section of floating ring bearing

图2 浮环轴承的有限元模型Fig.2 Finite element model of floating ring bearing

采用FLUENT中的Mixture多相流模型结合Cavitation空穴模型进行计算。在迭代过程中，将节点压力值与预先给定的相变压力阈值进行比较，实时判定该节点处的状态。

1.1 雷诺方程

浮环轴承内外油膜压力pi、po的雷诺方程分别表示为

(1)

(2)

式中：ωJ和ωR分别表示轴颈和浮环的角速度；ηi和ηo分别表示内、外油膜润滑油黏度；RJ和RR分别表示轴颈和浮环半径；hi和ho分别表示内层和外层油膜厚度，

hi=ci+eicosθi

(3)

ho=co+eocosθo

(4)

式中：ei和eo分别表示轴颈中心相对于浮环中心、浮环中心相对于轴瓦中心偏心距；ci和co分别表示内外径向半径间隙。

1.2 力矩平衡

浮环轴承一般应用于高速、轻载的转子系统中，除去自身重力之外，几乎不承受其他载荷，因此文中只考虑垂直向下的重力载荷。在稳定工况下，内外油膜合力分别与内外载荷幅值相等，方向相反。同时，内外油膜作用于浮动环上的扭矩也是幅值相等，方向相反。公式(5)、(6)和公式(7)分别表示力平衡方程和力矩平衡方程。

FXi=0，FYi=mJg

(5)

FXo=0，FYo=(mJ+mR)g

(6)

Mo+Mi=0

(7)

式中：FXi和FYi分别为内油膜在水平、垂直方向合力；FXo和FYo分别为外油膜在水平、垂直方向合力；mJ和mR分别为轴颈、浮动环的质量；Mi和Mo分别为内、外油膜作用于浮动环上的扭矩。

1.3 内外油膜温度平衡

内外油膜的摩擦功耗可由公式(8)计算得出。摩擦功耗所产生的热量将以对流、传导和辐射3种方式与外界进行热交换。对于浮环轴承而言，由于摩擦功耗的辐射散热量较小，几乎可以忽略不计，因而其所产生的热量主要以对流和传导的方式传播[18]。

(8)

式中：Ψi和Ψo分别为内、外油膜摩擦功耗；pi和po分别为内、外油膜压力分布；Ro为浮动环外径；ΩJ和ΩR分别为轴颈、浮动环角速度；L为轴承长度；μ为润滑油动力黏度。

Ψi=cpρQSIDEiΔTi+2πRJLλJ(ΔTi-ΔTJ)+2πRiLλR(ΔTi-ΔTR)

(9)

Ψo=cpρQSIDEoΔTo+2πRoLλR(ΔTo-ΔTR)+ 2πRBLλB(ΔTo-ΔTB)

(10)

2πRiLλR(ΔTi-ΔTR)=2πRoLλR(ΔTR-ΔTo)

(11)

式中：QSIDEi和QSIDEo分别为内、外油膜端泄流量；RB和Ri分别为轴瓦半径、浮动环内径；λJ、λR和λB分别为润滑油与轴颈、浮动环、轴瓦之间的热传导率；ΔTi、ΔTo、ΔTJ、ΔTR、ΔTB分别代表内、外油膜、轴颈、浮动环、轴瓦的温升；cp为润滑油比热容；ρ为润滑油密度。

由于公式(9)—(11)中的温升值均为未知量，无法直接通过能量平衡方程求出，因此须补充其他约束条件。根据热力学原理，轴承传导散热与对流散热之比取决于材料的热扩散率与摩擦副的接触情况，如公式(12)所示。

(12)

式中：ki和ko分别为内、外油膜传导对流散热比；α为热扩散率。

1.1 资料来源 回顾性收集、整理清城区1988-2017年疟疾疫情年报表、监测报表、防治工作总结、流行病学专题调查、中国疾病预防控制信息管理系统直报数据等。人口数据资料来自区统计年鉴。

将公式(12)与能量平衡方程(9)—(11)联立，即可求出ΔTi、ΔTo、ΔTJ、ΔTR、ΔTB等5个部分的温升。根据其中固体部分温升值与材料的热膨胀系数，即可计算浮环轴承新的内外间隙。

(13)

式中：γJ、γR和γB分别为轴颈、浮动环、轴瓦的热膨胀数；cio和coo为浮环轴承原内、外间隙。

浮环轴承的端泄温升取决于内外间隙的温升和端泄流量，如公式(14)所示。

(14)

式中：ΔTSIDE为端泄温升。

受端泄温升的影响，浮环轴承间隙内润滑油的温黏关系不可忽略。由于精确计算油膜中的温度分布十分复杂，文中采用有效黏度法推导润滑油黏度[12]。该方法认为轴承中在入口温度和出口温度之间存在一个有效温度，如公式(15)所示。通过Reynolds温黏关系模型，按公式(16)计算该温度下的有效黏度，作为计算轴承润滑性能的依据。

Tef=Tin+0.8(Tout-Tin)

(15)

式中：Tef、Tin、Tout分别为有效温度、入口温度和出口温度。

μ=μ′e-β(T-T′)

(16)

式中：T′为参考温度；η′为润滑油在参考温度下的动力黏度；β为温黏指数。

1.4 浮环轴承油膜端泄流量

浮环轴承内外油膜间的润滑油流动情况相对比较复杂。对于外层间隙来说，来自于轴瓦顶部注油孔注入的润滑油，一部分从外间隙两端流出，即端泄，一部分经过浮动环上均布的注油孔通过内外压力差流向内层间隙。对于内层间隙来说，润滑油来自于压差注油量，润滑油通过内层间隙的两端排出。在稳定工况下，流量达到平衡状态。从轴瓦注入的润滑油应等于内外间隙的端泄量之和，压差注油量应等于内油膜的端泄量[17]。

内油膜端泄流量：

(17)

外油膜端泄流量：

(18)

1.5 浮环轴承油膜摩擦功耗

内油膜摩擦功耗：

(19)

(20)

1.6 环速比

浮环转速ωR与轴颈转速ωJ的比值即为环速比

(21)

2 数值计算方法

采用流体力学软件FLUENT求解器进行油膜压力分布、油膜合力、端泄和浮动环扭矩的计算，利用其自定义函数接口(UDF)进行其他参数的求解，其中摩擦功耗的计算采用Simpson数值积分法完成。采用Newton-Raphson迭代法求解方程(1)—(21)，同时得到浮环轴承在某一工况下的静平衡位置、端泄流量、摩擦功耗、温升、间隙、浮环转速等运行参数。求解流程图如图3所示。

图3 计算程序流程Fig.3 Flow of the calculation program

3 理论模型验证

为了验证理论模型的正确性，根据文献[13]中的浮环轴承结构和润滑参数，对不同轴颈转速下的浮动环转速以及端泄温升进行了仿真计算，并将所得结果与实验数据进行了对比。表1列出了文中所用的主要仿真参数。

表1 主要仿真参数Table 1 Main simulation parameters

图4所示为不同润滑工况条件下，浮动环与轴颈转速之比在1 000～12 000 rad/s轴颈角速度范围内的变化情况。可见，除去个别转速点之外，仿真结果与实验数据基本吻合。

图4 不同润滑工况下的浮动环与轴颈角速度之比Fig.4 The speed ratio of floating ring and journal under different speeds：(a)oil supply temperature 37.8 ℃ and oil supply pressure 137 kPa；(b)oil supply temperature 37.8 ℃ and oil supply pressure 275 kPa；(c)oil supply temperature 26.7 ℃ and oil supply pressure 137 kPa

经过与文献[13]中实验数据的比对，验证了所建理论模型的正确性。为进一步探索浮环轴承在不同工况条件下的润滑特性，下文将仿真计算扩展至更宽的参数范围进行了分析。

4 计算结果与分析

在137 kPa供油压力和30 ℃供油温度情况下，探讨浮动环上圆周均布的油孔数目对浮环轴承的端泄温升、摩擦功耗、内外间隙、浮动环转速与端泄流量的影响。

图5和图6所示为油孔数目对浮环轴承摩擦功耗的影响。结果表明，内外油膜摩擦功耗与油孔数目的变化趋势相反；在较高的轴颈转速下，油孔数目增加，外油膜摩擦功耗增加，内油膜摩擦功耗减少。需要指出的是，在低速阶段，动压效应较弱，摩擦功耗也较低(温升不明显)，油孔的出现及数目的增加进一步消弱了动压效应，使得油孔数目的变化对轴承内外油膜功耗的影响不明显。因此，在轴径角速度为1 000和2 000 rad/s时，2孔、4孔、6孔浮环内外油膜的摩擦功耗相差很小，为0.02%～0.06%。

图5 油孔数目对外油膜摩擦功耗的影响Fig.5 Influences of the number of the oil holes on friction loss of outer oil film

图7给出了油孔数目对端泄温升的影响。油孔数目越少，内油膜端泄量越小，导致端泄温升越高；随转速的升高，不同油孔数目下轴承的端泄温升增大，其中在12 000 rad/s时，2孔和6孔浮环轴承的端泄温升已相差3 ℃以上。相比之下，由于动压效应较弱，在轴径角速度1 000和2 000 rad/s时，2孔、4孔、6孔浮环的内外油膜的端泄温升相差较小，为0.4%～0.7%。同时，较大的端泄温升也造成内外间隙的热变形加大，这种趋势进一步反映在图8和图9中。

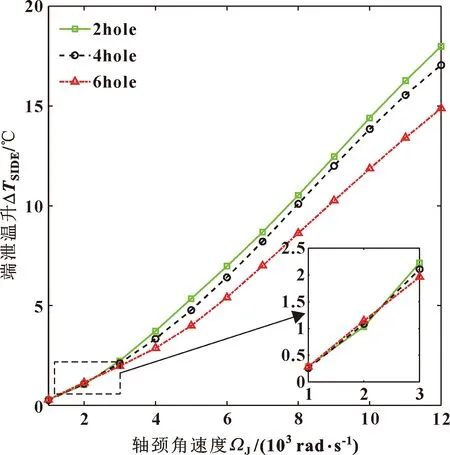
图7 油孔数目对浮环轴承端泄温升的影响Fig.7 Influence of the number of the oil holes on the temperature rise of side leakage

图8 油孔数目对内油膜间隙变化率的影响Fig.8 Influences of the number of the oil holes on change rate of inner clearance

图9 油孔数目对外油膜间隙变化率的影响Fig.9 Influences of the number of the oil holes on change rate of outer clearance

图10给出了油孔数目对浮动环转速的影响。在一定的轴颈转速下，油孔数目越多，内外间隙变形越小；作用于浮动环上的剪切力矩越大，浮动环转速越快。同时，在轴径角速度1 000和2 000 rad/s时，2孔、4孔、6孔浮环与轴颈角速度之比相差1.2%～1.6%。

图10 油孔数目对浮动环转速的影响Fig.10 Influences of the number of the oil holes on the speed of floating ring

图11和图12分别给出了油孔数目对浮环轴承内外端泄流量的影响。可以看出，油孔数目的增加会在一定程度上增加内油膜端泄流量，改善内油膜润滑；而对外油膜端泄流量的影响并不明显。同时，在轴径角速度1 000和2 000 rad/s时，2孔、4孔、6孔浮环的内外油膜的端泄流量相差相对较小，为0.8%～6.2%。

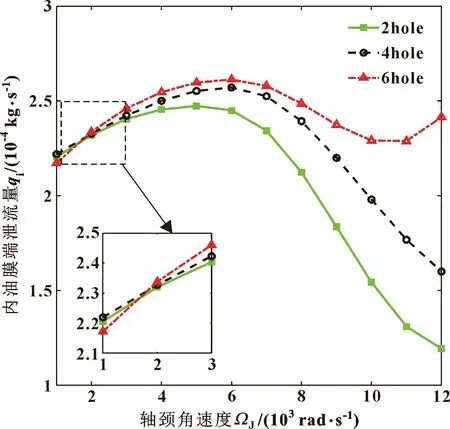
图11 油孔数目对内油膜端泄流量的影响Fig.11 Influences of the number of the oil holes on side leakage of inner oil film

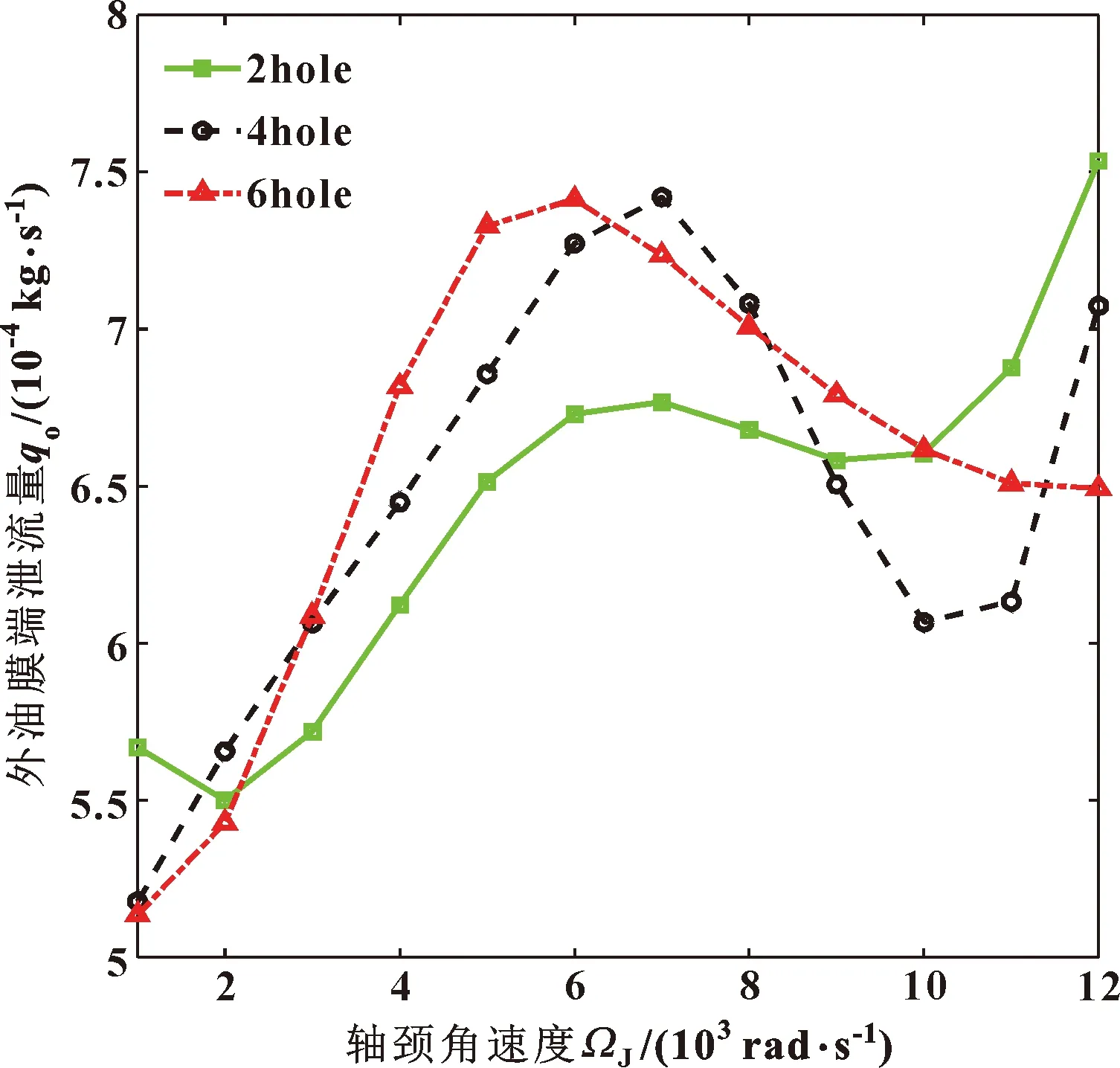
图12 油孔数目对外油膜端泄流量的影响Fig.12 Influences of the number of the oil holes on side leakage of outer oil film

5 结论

(1)在相同的润滑工况下，浮动环上均布的油孔数目越多，端泄温升越小，内外间隙变形越小，浮动环转速越快。

(2)浮动环转速的增加小幅提升了轴承内间隙润滑油的注入量；相比之下，内油膜端泄流量受油孔数目变化的影响较大，而外油膜端泄流量几乎不受影响。