某型飞机尾橇缓冲装置阻尼油孔设计及优化

吴晓宇

(上海飞机设计研究院，上海 200135)

0 前言

根据运输类飞机适航条款CCAR25.107的要求，必须确定飞机的最小离地速度，在等于和高于该速度时，飞机可以安全离地并继续起飞。某型飞机承担最小离地速度试飞科目，但因其是“按几何设计”的飞机，在进行该试飞科目时因飞机抬头过高会造成尾部触地，如图1所示，所以需要在飞机尾部下表面加装特殊的缓冲装置以保护飞机本体结构不受到损坏。

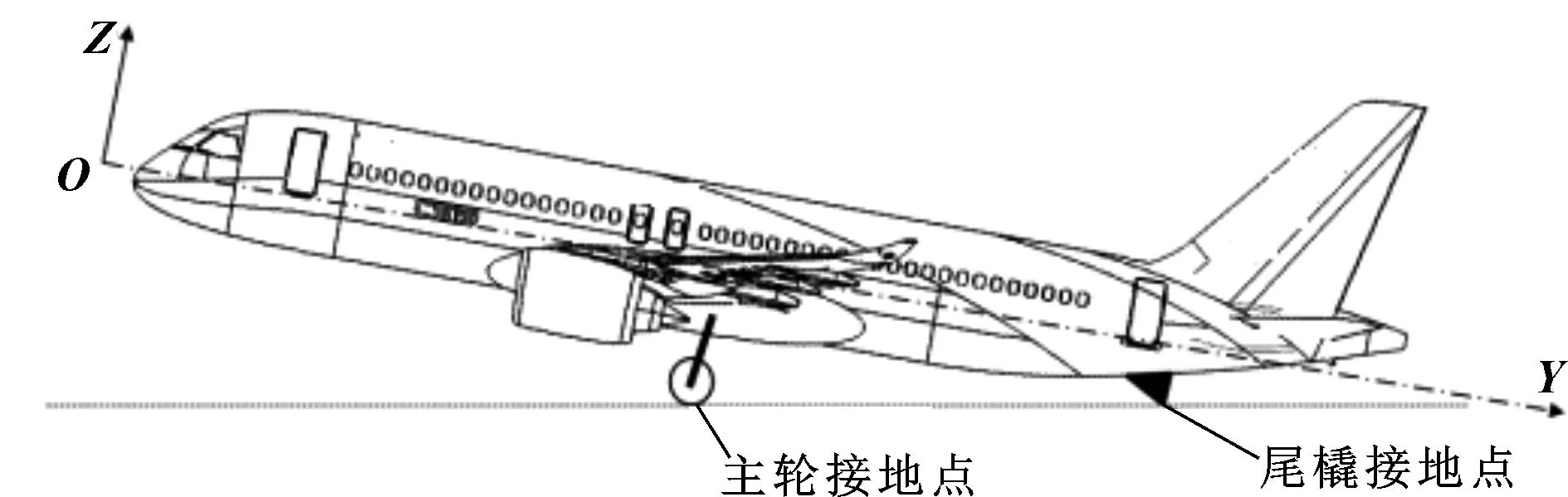
图1 飞机最小离地速度试飞接地示意

尾橇缓冲装置主要用于承受和耗散飞机在最小离地速度试飞科目时尾部与地面的撞击能量，因此该装置的缓冲性能极为关键。通过对其阻尼油孔的特殊设计和优化，可以降低阻尼峰值，提高缓冲效率。

1 阻尼油孔有效面积的计算方法

尾橇系统作用是飞机在进行最小离地速度试飞科目时保护飞机尾部结构，因此，需要尾橇系统在所有试飞条件下均满足要求。取最大起飞质量工况作为极限验证工况，如表1所示。

表1 最小离地速度试验极限工况

飞机在执行最小离地速度()试飞任务时，尾橇缓冲器可在触地后吸收飞机转动而产生的能量。为了使机体结构受到的载荷最小，在整个缓冲行程中阻尼力保持恒定时，缓冲效率最高，此时阻尼力峰值最低。而阻尼力与油孔的大小有关，因此需选取油孔有效面积随行程变化的设计方式。

假设已知尾橇所受的当量质量和初始冲击速度，则需要被吸收的飞机转动能量可转化为

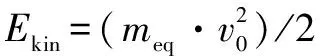
(1)

式中：为飞机转动能量；为当量质量；为初始冲击速度。

为了在缓冲行程中吸收该能量，阻尼力作的功需要与之相等，随后将其转化成热量耗散。由于需要降低峰值载荷，因此最佳的阻尼力为一个不随时间和行程变化的恒定值。在最大缓冲行程下最优化的阻尼力为

=/

(2)

式中：为阻尼力；为最大缓冲行程。

在这个阻尼力的作用下，缓冲器压缩速率为线性变化，随时间变化如下：

()=-·

(3)

式中：()为缓冲器压缩速率。

上式等号两边对时间进行积分(=0时，=)，得到行程随时间变化的公式:

=-(2)·+·+

(4)

式中：为缓冲行程；为缓冲器初始行程。

已知初始条件()=和(=0)=0，将式(3)和式(4)中时间消去，得到速度和行程之间的关系：

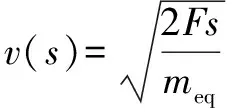
(5)

在压缩过程中的有效压油面积为，则缓冲器高压油腔中的压力为

=

(6)

式中：为高压油腔的压力；为压油面积。

由于低压油腔中的压力与高压油腔中的压力相比可以忽略不计，则可由流量公式推导油孔有效面积的变化公式：

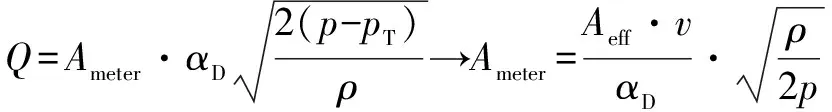
(7)

式中：为油孔的缩流系数；为油孔的有效面积；为低压油腔的压力；为油液密度；为缓冲器压缩速率。

由式(7)可以看出与速度成正比关系，将式(5)和式(6)代入可以推导得出与行程的关系如下：

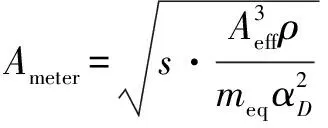
(8)

由式(6)和式(7)可得阻尼力公式为

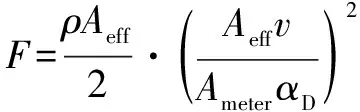
(9)

2 油孔初步设计方案

将极限工况的参数代入公式(1)中计算可知，尾橇缓冲器必须能够吸收飞机转动能量为23 816.96 J，以此作为缓冲器设计的基准。除了油孔参数以外，缓冲器还有其他设计参数，见表2。

表2 某型飞机尾橇缓冲器参数

该尾橇缓冲器采用套筒式变油孔，其结构型式如图2所示，采用双侧对称布置，图中仅显示了一侧油孔。

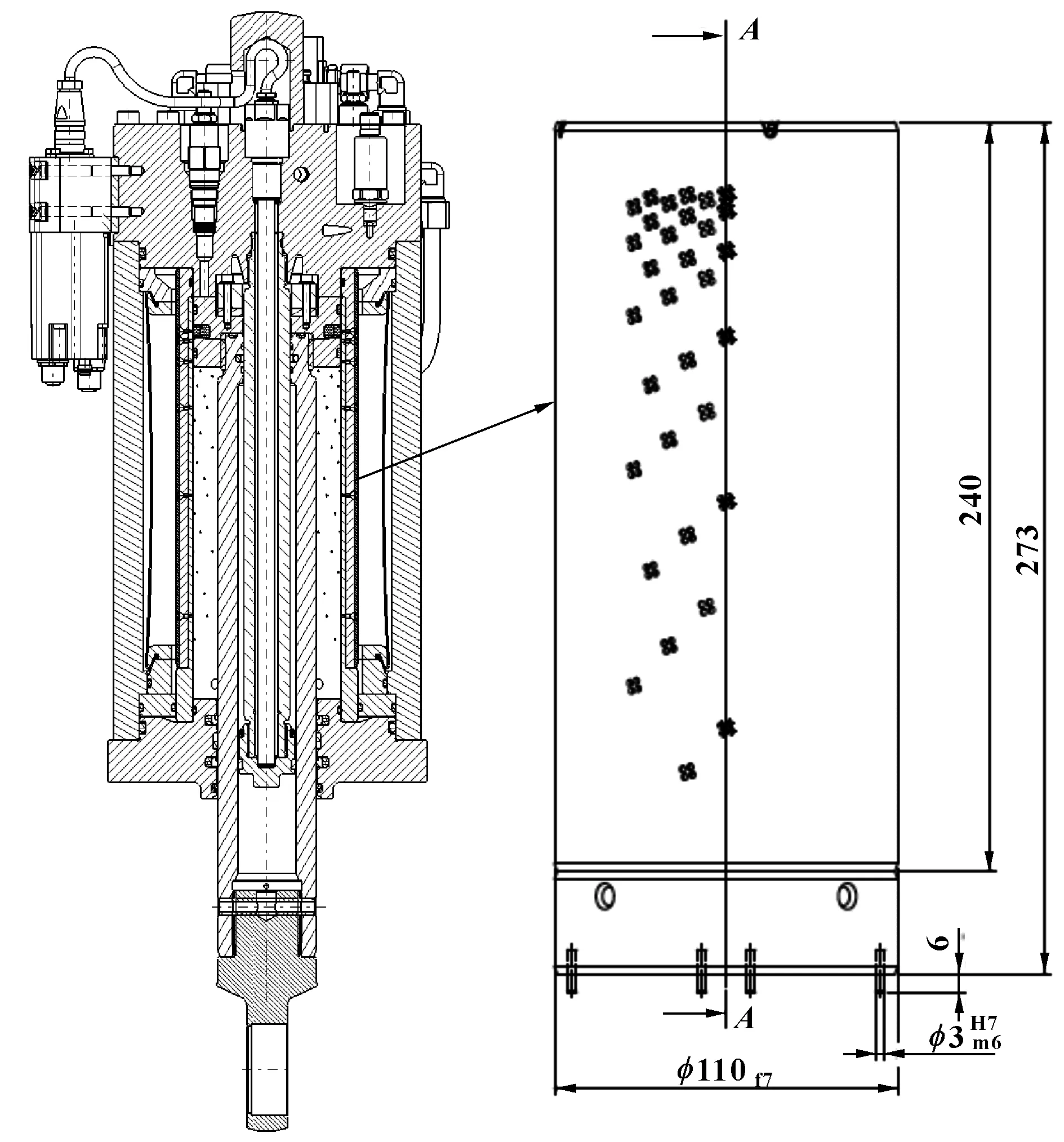
图2 套筒式变油孔

这种型式的变油孔的特点是使用“等直径变距离”分布式油孔，整个油孔套筒构成了缓冲器外筒。它的工作原理是随着缓冲器的压缩，油液被挤压流过油孔产生阻尼力。随着缓冲器的压缩，位于活塞下端的油孔越来越多，而活塞上端的有效油孔面积则越来越小，此时行程速度不断减小。将有效油孔面积按公式(8)设计可使其与行程速度成正比关系，从而通过公式(9)可知此时阻尼力为恒定的值，此时缓冲效率最大，阻尼峰值最小。

缓冲器行程定为200 mm，设定单侧油孔数量为30个，油孔直径初步选取1.1、1.2和1.3 mm(3个直径进行比较后选择最优值)。由公式(8)可知行程与油孔有效面积之间的函数关系，可以在行程范围内得到图3所示的曲线。

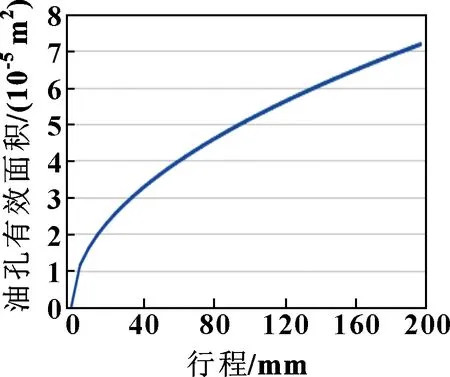
图3 行程与油孔面积变化曲线

当油孔直径取1.1 mm时，最大油孔面积为5.701 99×10m，将其代入上述曲线中可得最大行程为127 mm；

当油孔直径取1.2 mm时，最大油孔面积为6.785 84×10m，将其代入上述曲线中可得最大行程为180 mm；

当油孔直径取1.3 mm时，最大油孔面积为7.963 94×10m，将其代入上述曲线中可得最大行程为248 mm。

综上可知，油孔直径取1.1 mm时，使用行程占用率太低，而取1.3 mm时最大使用行程超过缓冲器行程200 mm，因此油孔直径取1.2 mm最为合理。

当油孔直径取1.2 mm，单侧油孔数量取30个，可得到活塞杆从最大行程向行程末端方向移动时，未覆盖单侧油孔数量与剩余油孔面积的变化关系，再将油孔面积代入图3中的曲线反求位移值，可以得出表3中的各参数值。

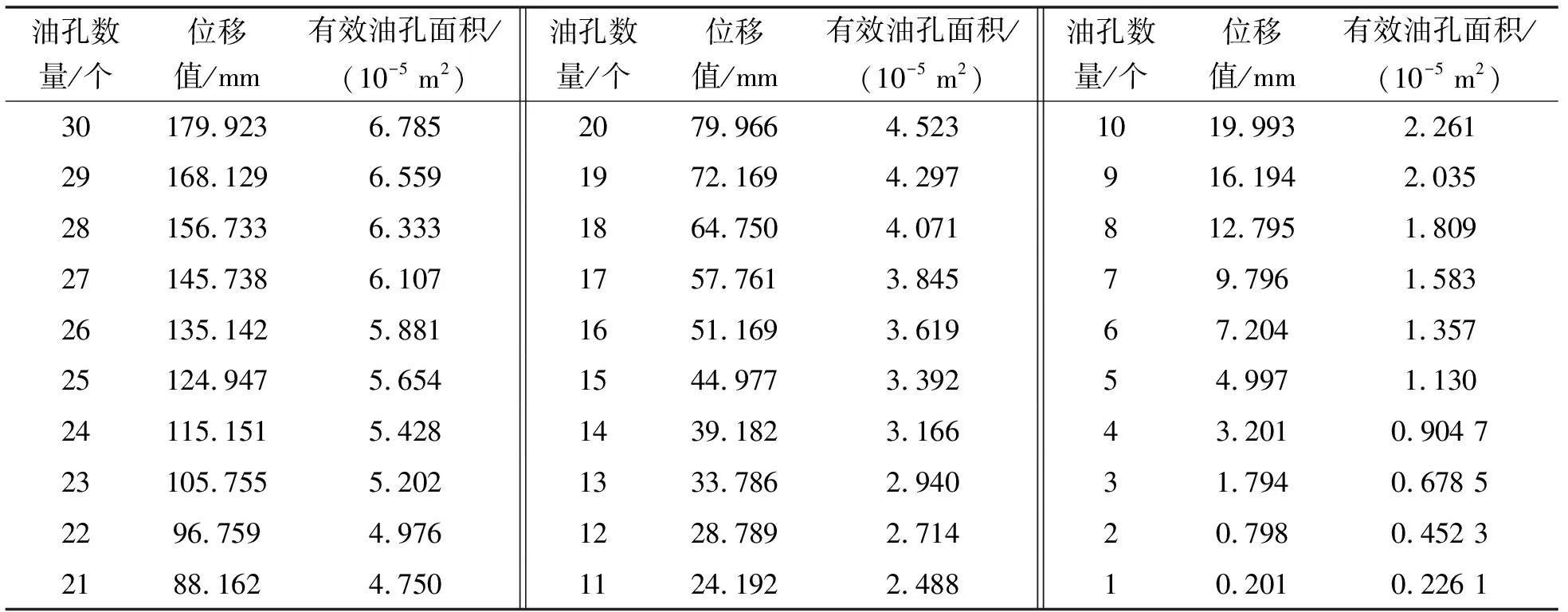
表3 有效油孔面积与位移对照

利用以上参数，基于MSC.ADAMS和AMESim联合仿真平台搭建尾橇缓冲性能分析模型，如图4所示。

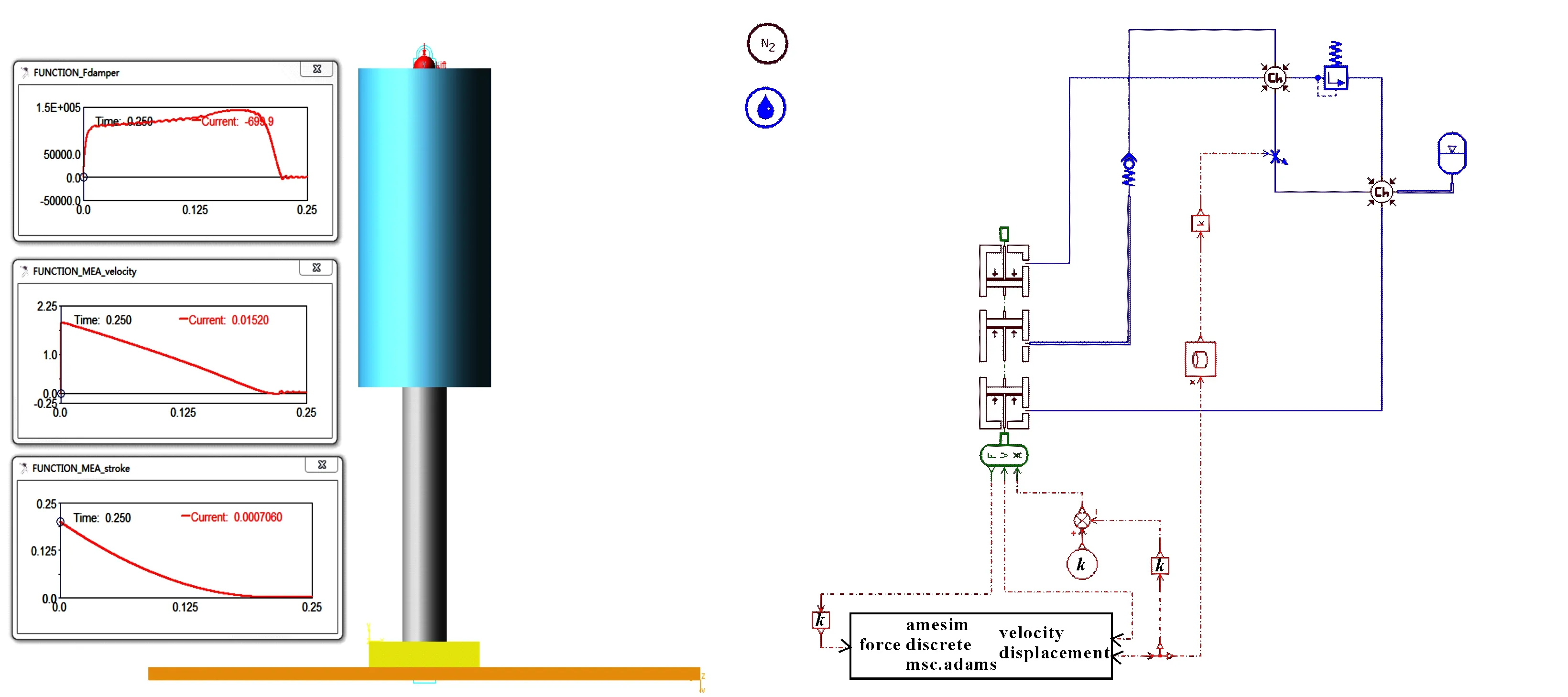
图4 基于MSC.ADAMS和AMESim的联合仿真模型

通过仿真计算可得出如图5所示的功量曲线，可知缓冲器效率仅为80%左右，低于设定的目标效率(100%)较多；阻尼力随行程变化较大，峰值较高(缓冲器工作过程中的油液阻尼力峰值为1.538 1×10N)，不满足设计要求。

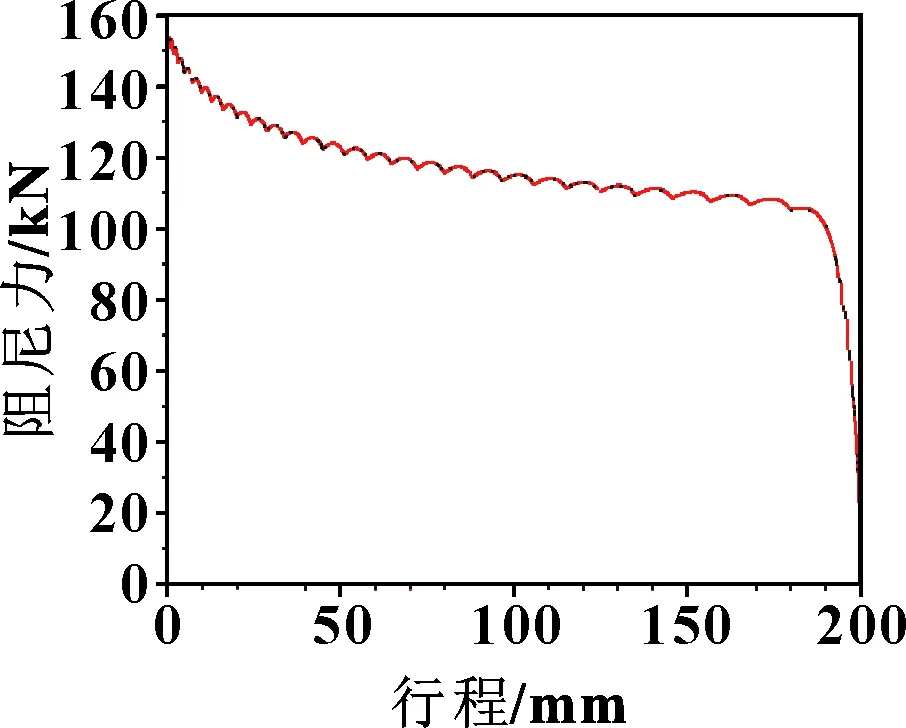
图5 油液阻尼力随行程变化曲线(功量图)

分析图5可知：油液阻尼力在行程初期(200 mm)较小，在行程末端(0 mm)陡升。因此油孔面积优化的方向为：在行程初期适当减小，在行程末端适当增大。而油孔直径和数量一定，面积也一定，因此作者选取的优化策略为：油孔面积、数量不变，而改变在对应油孔面积下的行程(即表2中的位移值)。

在优化油孔面积分布的时候需要考虑的原则有：(1)油孔面积最大处的位移值不能超过200 mm；(2)油孔面积最小处的位移值不能低于0 mm；(3)保持行程与油孔有效面积变化曲线平滑度，尽量避免出现凸峰或凹峰。

3 优化油孔参数

根据优化方向和优化原则对油孔分布进行调整，选择的方案为不改变油孔面积和数量，仅将对应有效油孔面积的位移值增加10 mm，如表4所示。

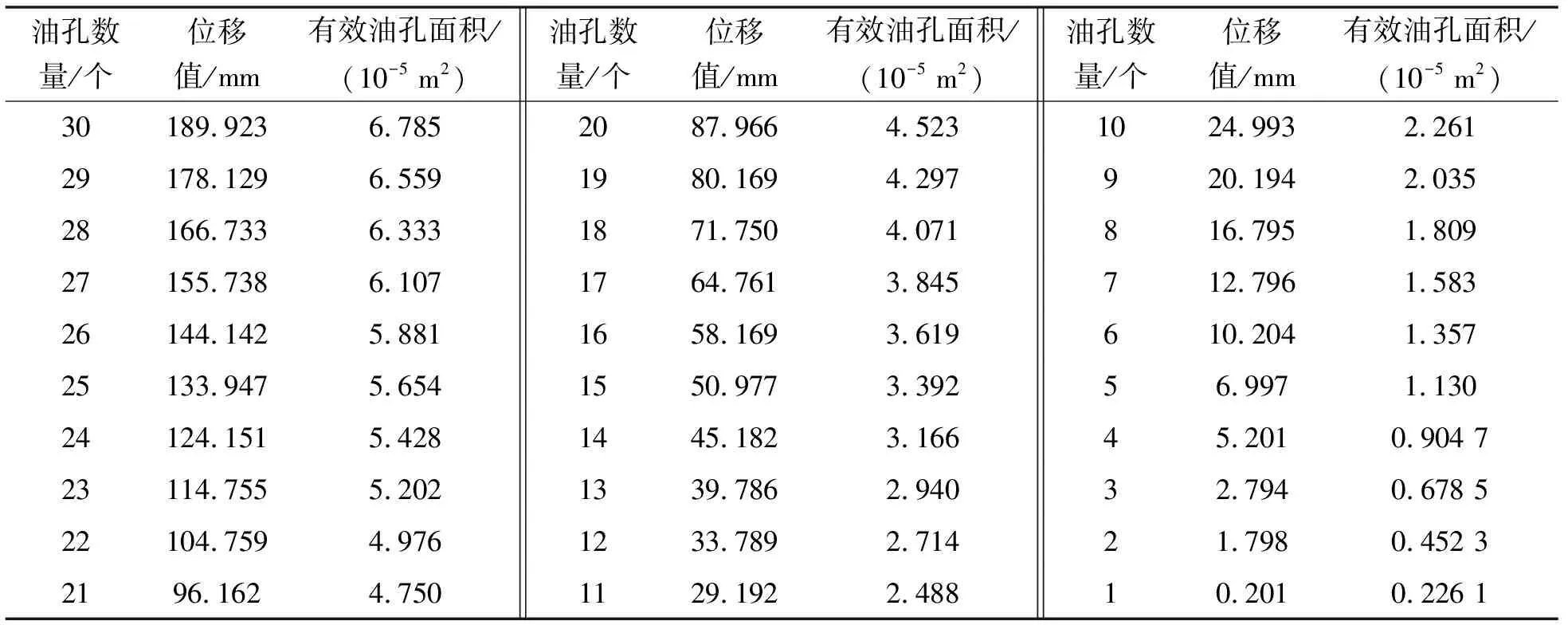
表4 优化后的有效油孔面积与位移对照

利用优化后的参数进行联合仿真计算可得到如图6所示的功量曲线，可知：缓冲器效率为93%左右，接近设定的目标效率(100%)；阻尼力随行程变化较为平缓，峰值较低(缓冲器工作过程中的油液阻尼力峰值为1.302 6×10N)，基本满足设计要求。

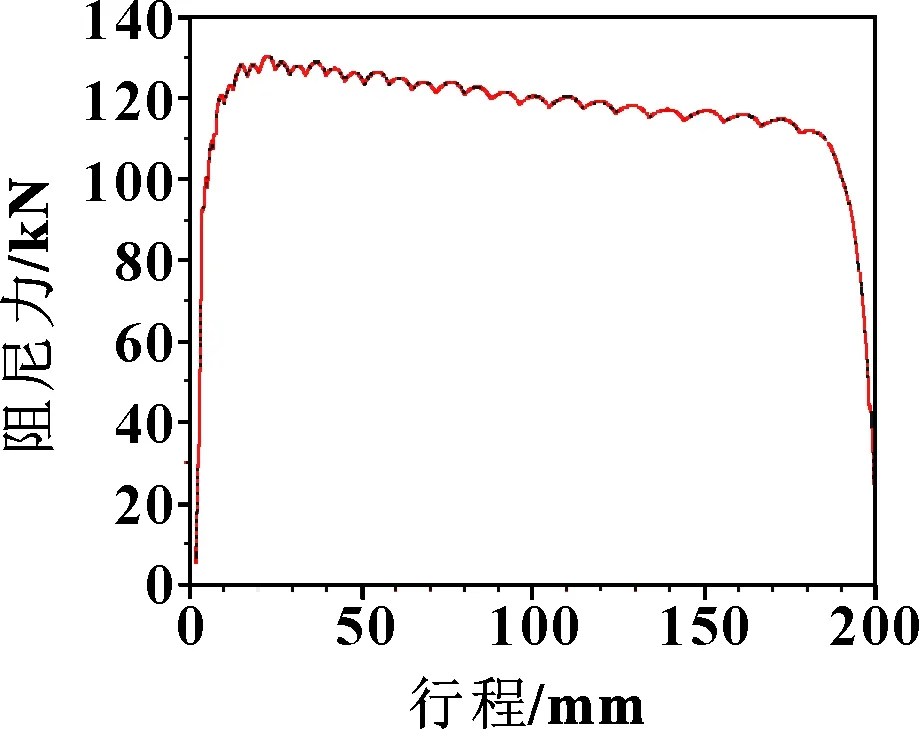
图6 优化后的油液阻尼力随行程变化曲线(功量图)

经过上述优化，可以得到一套基本满足效率和载荷峰值要求的油孔布置方案。优化前后的参数对比如表5所示。

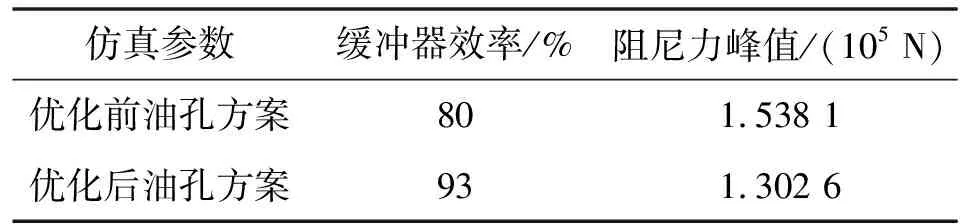
表5 优化前后的参数对比

由结果可得，优化后峰值载荷减小15.3%，效率增加了16.25%，该油孔优化方案合理有效。

4 结论

(1)提出一种新型的阻尼油孔设计方案，并应用在尾橇缓冲装置上；

(2)研究变油孔的设计方法并通过计算公式说明其原理；

(3)采用该设计方法设计了一套“等直径变距离”的分布式油孔，形成了一个套筒式尾橇阻尼油孔方案；

(4)利用MSC.ADAMS和AMESim联合仿真搭建了尾橇缓冲性能分析模型并进行了缓冲性能仿真分析和优化，发现优化后峰值载荷降低15.3%，缓冲效率增加16.25%。该优化方案合理有效，为分布式变油孔优化设计提供了一种切实可行的方法。