一种采用动态补偿的五轴机床铣削力预测方法

王胜曼，牛博英，孙晓燕

(保定理工学院,河北保定 071000)

0 前言

五轴数控机床的灵活度高，可加工较复杂的工件。随着人们对工件加工要求越来越高，五轴数控机床已被广泛应用。在五轴数控机床加工工件的过程中，其切削力与工件加工质量息息相关。

为获取较理想的工件，人们对数控机床的铣削力进行了预测。LUO等建立了一种新的曲面端铣切削力解析模型，考虑到刀具几何参数的变化，采用法向摩擦角、法向剪切角、切屑流动角和剪切应力等物理参数表征切削力系数，以斜向切削模型为基础，利用最小能量原理，建立了各物理参数之间的数学关系；采用牛顿迭代法求解所建立的非线性方程组，标定切削力系数，进而实现对切削力的预测。文献[5]通过对切削刃单元平移和旋转的精确分析，推导出未变形切屑厚度，并采用基于切削刃单元分类的设计方法确定切屑厚度；然后，利用所提出的切削刃单元模型和刀具切削力的确定方法，建立了切削力模型。CAI等提出了一种基于非均匀有理基样条和有限元法的切削力预测模型，对不同参数下的单刃切削力进行了有限元模拟，并采用非均匀有理基样条插值方法建立了单刃切削力模型；结合刀尖运动模型，对多刀面铣刀的切削力进行预测。这些方法实现了对切削力的预测，但是预测精准度不高。

对此，本文作者分析五轴数控铣削加工中心进给传动动力学，建立测量扰动频率响应的状态空间模型。通过卡尔曼滤波器求取切削扭矩的估计值，进而实现对切削扭矩的动态补偿。在Denavit-Hartenberg方法的基础上，将刀具坐标系中的刀尖力映射为驱动力矩，完成切削力的预测。通过对比加工过程中实测力信号与预测力信号的吻合性，分析所提方法的有效性。

1 五轴数控铣削加工中心进给传动动力学分析

在五轴数控加工中心中，有3个滚珠丝杠驱动的平动轴(、、)和2个旋转驱动带有蜗轮传动的机构(、)，外部PC机通过以太网与机床进行实时通信。五轴数控加工中心如图1所示。

图1 五轴数控铣削加工中心示意

在图1中，外部PC机通过以太网可直接从数控机床获得刀具中心点的指令及实际位置、速度、加速度、指令电机电流值。机床的进给速度和主轴速度可以直接从外部PC机进行控制，以便实时监控和控制加工操作。

进给驱动电机必须克服机床中的静态和动态负载。静载荷包括进给传动运动链(即滚珠丝杠、推力轴承、导轨)中的摩擦力，而动态载荷则由加速度和作为转矩扰动传递给进给驱动电机的切削力组成。电机传递的总转矩与刷毛弯曲产生的摩擦力矩和测量切削扭矩有关，其计算公式为

(1)

式中：为电机转矩常数；为电机电流；为电动机的等效惯量；为电机轴角速度。

与摩擦界面内弹性刷毛的刚度和阻尼系数有关，其表述为

(2)

式中：为黏滞摩擦系数；为相对速度；为刷毛的平均挠度。

Stribeck效应和库仑摩擦力矩及静摩擦力矩有关，其计算公式为

()=+(-)e-()

(3)

平动进给驱动电机的转矩，由切削力转换而来，其计算公式为

(4)

式中：为节距长度；为滚珠丝杠传动比；为转换效率。

切削力被传送到机器的旋转驱动装置上时，其产生的切削扭矩为

(5)

式中：为刀尖和工作台中心之间的力臂长度,=,,。

切削力通过驱动器的结构链和伺服放大器作为干扰力矩传递给进给驱动电机。在铣削过程中，切削力是周期性的，其频率等于主轴转速乘以刀具上的齿数。在通过以太网连接测量数控机床的电机轴电流和角度时，在工作台上施加冲击力激励，以测量扰动频率响应()，该传递函数可表述为

(6)

式中：和n分别为模态下电机轴的阻尼和固有频率。

式(6)可以映射为关于每个轴的多项式形式：

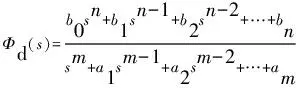
(7)

式中：、为多项式参数。

将式(6)和式(7)中给出的扰动传递函数映射到状态空间，并通过状态、输入、输出和输入传输矩阵得到其状态空间模型为

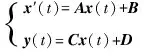
(8)

式中：()和()分别表示状态向量和输出向量。

采用状态空间模型对测量电流进行卡尔曼滤波，可估计主轴转动时，进给驱动电机上的力引起的切削力矩。

2 切削扭矩的动态补偿

结构动态模式会使包含频率高于伺服带宽的测量值失真，为减少结构动态模式的影响，需要进行切削扭矩的动态补偿。本文作者利用卡尔曼滤波器衰减噪声并补偿结构动态模式对间隔采样的切削力矩的影响。

作用在刀具上的实际切削力，被式(6)中的扰动传递函数所控制的进给驱动系统的结构动力学所扭曲。卡尔曼滤波的目的是通过去除式(6)中的扰动动力学效应，重建切削力产生的实际切削扭矩。在传动装置中，实际切削扭矩由直流(静态)分量和交流(谐波)分量叠加而成。

切削力矩的谐波分量，在具有周期性干扰噪声的Laplace域中可以表示为

(9)

式中：为齿传递频率。

式(9)对应的状态空间模型为

(10)

综合式(8)—式(10)可得：

(11)

式中：和分别为扩展状态空间模型的状态和输出矩阵；()和()分别为过程噪声项和测量噪声项；为系统噪声矩阵；和分别为直流和交流噪声比项。

从式(11)可见的切削部分取决于扰动动力学矩阵和、过程噪声项和测量噪声项()和()。

(12)

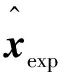
通过式(12)可得出卡尔曼滤波器的传递函数：

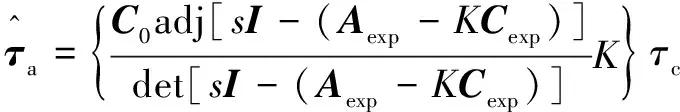
(13)

协方差矩阵的微分方程可通过和求取：

(14)

式中：测量协方差矩阵由空气切割扭矩波动的均方根确定，而系统协方差矩阵则被调整以适应补偿。

3 用于力转换的机床运动学建模

在机床工作期间,刀具的运动取决于3个平动轴和2个旋转驱动的传动机构。为将估计的切削力矩从各轴电机的电流转换到相对于机床工作台中心的刀具中心位置，在Denavit-Hartenberg(D-H)方法的基础上，对机床的运动学进行建模。

(15)

中的刀具定位可以通过以下公式计算：

(16)

利用D-H方法从刀尖位置计算平动驱动器轴位置的公式为

(17)

其中：和为旋转驱动坐标系之间的线性偏移量；s和c分别为正弦(sin)和余弦(cos)项。通过对齐次D-H变换矩阵进行逆计算，将中的刀尖位置表示为中的轴位置函数

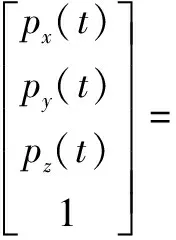
(18)

雅克比矩阵用于定义施加在工具上的力和驱动装置上的扭矩之间的关系。通过虚功原理可知在静平衡时，工件空间(外部)和驱动空间(内部)所作的虚功应相等，因此给定工件框架和驱动框架中刀具的微小位移和驱动框架所作的功应该相等，即：

(19)

式中：为包含作用在工件框架中刀具上的切削力和扭矩的矩阵；为包含驱动框架中驱动力和扭矩的矩阵，其公式分别为

(20)

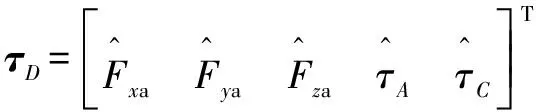
(21)

根据雅克比矩阵，式(19)可改写为

(22)

式中：为雅克比矩阵，其表达式如下：

(23)

联合式(20)—式(22)可得和的关系式：

(24)

由式(24)可知，刀具坐标系中的刀尖力映射为驱动力矩的过程为

(25)

4 实验结果

在Quaser UX600五轴联动机床上，利用Kistler测力仪采集力信号。同时,利用MATLAB/Simulink建立仿真环境,对文中方法进行力预测实验，以检测该方法对机床加工过程中力预测的精准性。实验平台如图2所示。

图2 实验平台

4.1 力预测测试结果

在加工过程中，随机截取一段时间内实际测量的力信号，与该时间段内的预测力信号相比较，以分析文中方法对五轴机床力预测的精准性。实测力信号与预测力信号如图3所示。可知：在1～6 s内，实测力信号与预测力信号基本相符；但在第6 s附近，实测力信号与预测力信号稍有偏差；在6～12 s内，预测力信号几乎与实测力信号一致，仅有两处细微的力信号偏差，主要是因为加工环境引起的颤振所致。由此可见，文中方法能够较精准地预测五轴数控机床加工时需要的力信号，能为提高数控机床加工工件的质量提供有力保障。

图3 实测力信号与预测力信号

4.2 电流测试结果

为进一步观察文中方法的有效性，对力预测测试时间段内(2～12 s)电机电流的实测信号与预测信号进行对比。电机电流的实测信号与预测信号如图4所示。

图4 实测电流信号与预测电流信号

由图4可知：实测电流信号与预测电流信号的相似度非常高，预测电流信号与测试电流信号仅在第10、12 s附近出现了些许偏差。由此说明，文中方法能够有效预测出加工过程中电机所需的电流信号，从而精准地实现力预测。

5 结论

本文作者在分析五轴数控铣削加工中心的结构后，对它进行了进给传动动力学分析。然后，通过卡尔曼滤波器对每个驱动装置的结构模态引起的干扰进行了补偿。采用Denavit-Hartenberg方法对五轴数控机床进行运动学建模，并将补偿后的切削扭矩转换到刀具坐标系中，得到切削力。通过对比实测力信号与预测力信号发现，文中方法预测的力信号与实测力信号的吻合度较高，表明文中方法能够精准地预测出五轴机床的铣削力。