轴承圆度误差测量不确定度GUM法和MCM评定分析

张珂，苏凯伦，成果

(上海应用技术大学，上海 201418)

0 前言

轴承是回转机械中的重要传动支撑件，在机床、飞机、航天器等精密机器和设备中应用广泛；轴承的精度决定了设备的精度，进而影响整台机械设备的性能，因此正确而精准地表达出轴承的圆度误差十分重要。

在测量领域，如果“测量结果”仅表示测量量的估计值并不是十分准确，还应使用测量不确定度表示测量结果的可信程度，即在评定轴承圆度误差时，还应给出相应测量不确定度。目前，使用和研究较多的测量不确定度评定方法为《测量不确定度表示指南》(Guide to the Expression of Uncertainty in Measurement，GUM法)和蒙特卡洛法(Monte Carlo Method，MCM)。

目前测量不确定度方面有很多研究，窦光武等研究了道路动态弯沉计算因子测量不确定度；PUEO等给出了估算双面齿轮滚动试验测量不确定度的一般表达式；GUILLORY 等研究了多点坐标测量系统样机的不确定度评定；神经网络、支持向量机等方法评定测量不确定度也有相关研究；MIURA、WANG 等在蒙特卡洛法评定测量不确定度方面有很深的研究。但以上研究大多是使用单一方法评定圆度误差测量不确定度；或在测量风速等其他领域研究GUM法和MCM评定测量不确定度对比。因此，为分析GUM法和MCM在评定轴承圆度误差测量不确定度实际应用领域的情况，本文作者采用这两种方法进行评定，综合分析每种方法在轴承圆度误差评定领域的适用范围、可操作性、可信度等。

1 圆度误差评定

首先对圆锥滚子轴承33009型外圈(外径公称尺寸75 mm)进行实际测量，获取坐标数据。本文作者使用三坐标测量机获取零件坐标信息，型号为德国蔡司CMM PRISMO 9/13/7 ultra型，对轴承外圈大端面13 mm处进行测量，选取均匀分布的38个测量点，测量情况如图1所示。

图1 轴承外圈实测情况

测量数据如表1所示。

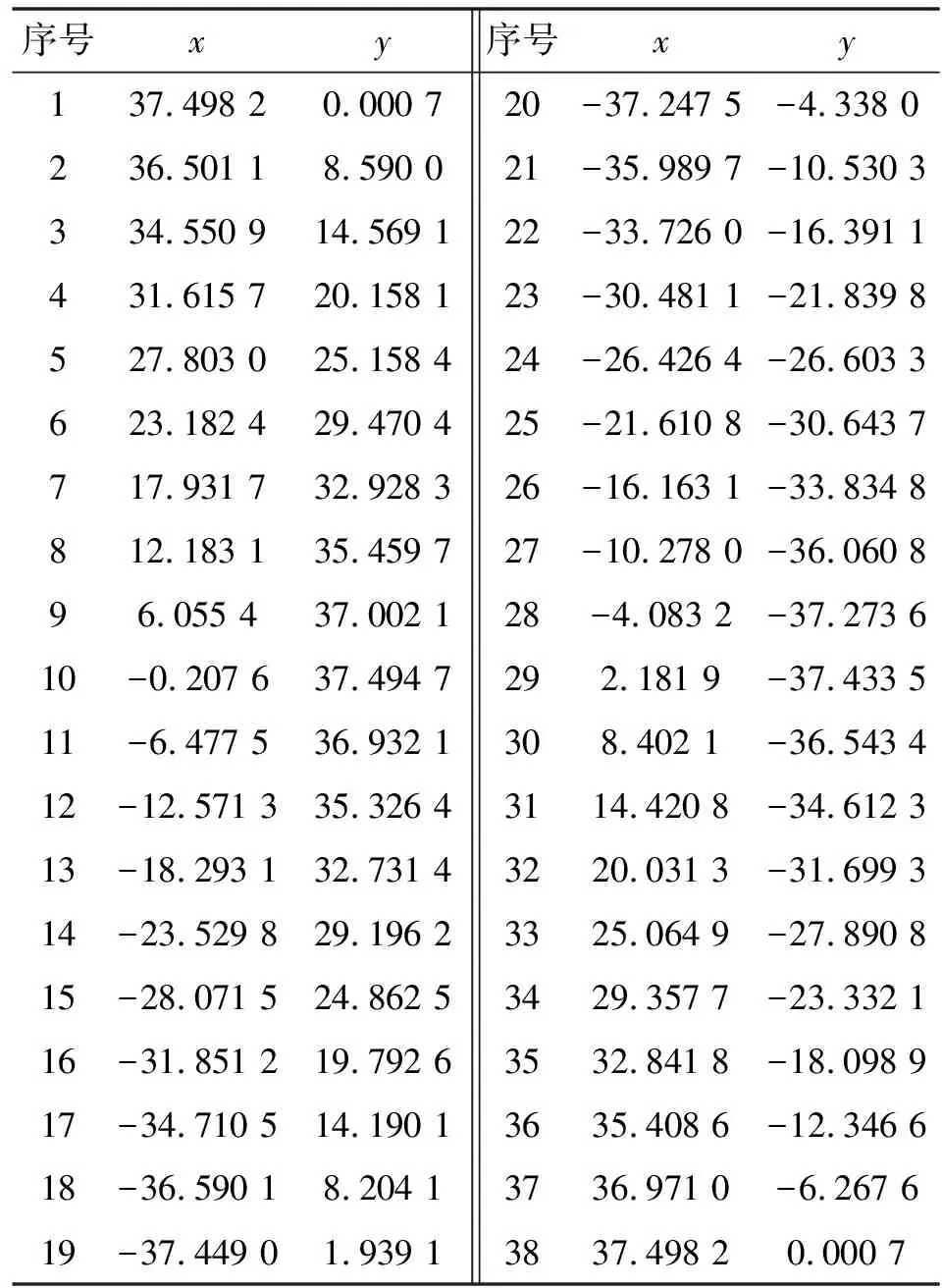
表1 三坐标测量机实测数据 单位：mm

基于方法简便程度和工程应用成熟度的考量，本文作者采用最小二乘拟合圆法进行评定。将实测获取的采样点测量值(,)进行最小二乘拟合，得到圆心坐标(,)，拟合目标可表示为

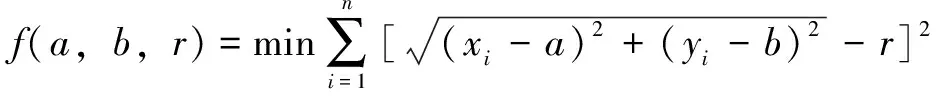
(1)

距离拟合圆圆心最远点坐标为(,)，距离拟合圆圆心最近点坐标为(,)，因此，圆度误差可表示为

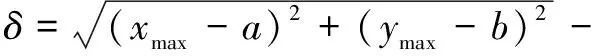
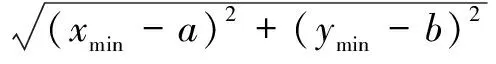
(2)

使用MATLAB对表1测量值进行最小二乘拟合，具体结果如表2所示。

表2 最小二乘拟合结果

2 测量误差不确定度评定

2.1 GUM法

采用GUM法评定测量不确定度的流程如图2所示。

图2 使用GUM法评定测量不确定度的流程

2.2 单批次MCM

(1)最小二乘模型式(2)中有、、、、、六个变量，其中、、、的测量值由表2可知，不确定度分别为、、、，可根据三坐标测量机的不确定度来源得到；、的值可由式(3)求得，其不确定度为、。

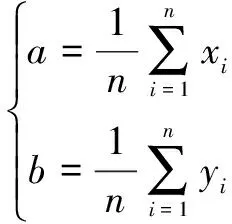
(3)

(2)、、、、、可以通过MATLAB生成的六维随机数组进行模拟，随机数组根据变量的期望和方差值获得，样本量越大越可以使结果更具真实性。利用MATLAB的随机数生成命令，生成期望分别为、、、、、，方差分别为、、、、、的正态分布随机数组。

(3)将得到的数据代入式(2)得到个圆度误差为的值，构造概率分布，判断分布类型，求出其期望和方差，期望即为圆度误差的值，方差值即为所要求的圆度误差测量标准不确定度。

2.3 自适应MCM

(1)选择所需的包含概率；

(2)选择不确定度()的十进制数字的个数=1；

(3)给出变量所进行的蒙特卡洛实验的批数；

(4)对于第批次蒙特卡洛实验，执行次蒙特卡洛实验，计算得到个模型值,…,，并计算出、()、、；

(5)每批次试验后计算参数的平均值和标准偏差

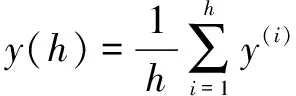
(4)

(5)

(6)设定数值容差，为标准不确定度最后一位有效数字下一位的一半；

(7)进行稳定性判断，当()、()()、()、()均小于2时，则表明达到统计学的稳定，评定结束；否则+1，返回步骤(3)。若所有的结果达到稳定，利用×个模型值计算、()和100概率包含区间。

2.4 MCM验证GUM法

(1)用GUM法得到输出量的概率的包含区间±，此处为约定包含概率；

(2)用自适应MCM获得输出量的标准不确定度()和最短包含区间的端点值和；

(3)通过式(6)、式(7)确定两个包含区间各自端点的绝对偏差，如果和不大于，则GUM法可以通过验证。

=|--|

(6)

=|--|

(7)

3 评定结果

3.1 GUM法

以表1测量值为例，先计算单点不确定度。分析合成单点不确定度的来源，过程如下：

(1)实验时对单点坐标重复测量10次，即=10，不确定度分量可由下式求得

(8)

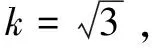
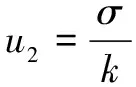
(9)

(3)测试时，室温恒定保持在20 °C，因此温度引起的不确定度近似为0。

(4)在实际测量中，测力变形引起的不确定度分量近似为0。

(5)合成单点不确定度由下式得出

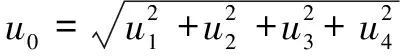
(10)

(6)实际测量中测量环境相同，各测量点的不确定度也相同均等于合成单点不确定度：====

(7)拟合圆心坐标(,)的不确定度、可通过下列两个式子计算得到

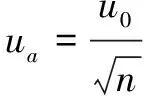
(11)

(12)

(8)实际测量中，测量点较多，和的相关系数近似为零，即=0，合成标准不确定度见下式：

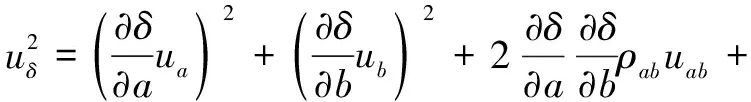
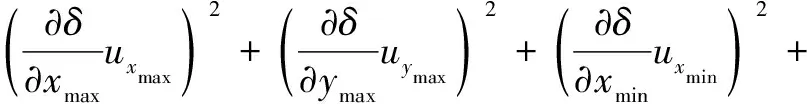
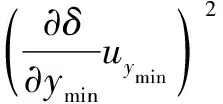
(13)

(9)选取95%的包含概率区间，区间因子=1.96计算结果如表3所示。

表3 GUM法计算结果

3.2 单批次MCM

使用MATLAB软件里自带的函数生成随机数，由此可得每组随机数的期望和方差，期望即为所需的实验测得值，方差即为各参数的单点不确定度。使用MCM产生足够多的圆度误差数据，仿真结果见表4。

表4 单批次MCM结果 单位：μm

3.3 自适应MCM

(1)设定、、、、、的分布为正态分布；

(2)设置包含概率为95%，批次内运行次数=10 000，设定=1，对应数值容差=0.5×10；

(3)设定循环次数=1；

(4)设定随机抽取样本数=10 000，当=1和=2时，执行两个单批次MCM实验，取得相应实验数据，并获取各自的最佳估计值、标准不确定度和95%概率的包含区间；

(5)当执行完两个单批次MCM后，达到了稳定状态。

仿真结果如表5所示。

表5 自适应MCM结果 单位：μm

4 对比评定

GUM法是基于中心极限定理而衍生的方法，因此，不论输入量的分布是否为正态分布，输出量的分布类型一定可以近似为正态分布或者近似为分布，即在GUM法中，输出量的分布类型不受输入量分布类型改变的影响。

而在MCM中，输出量的概率密度分布受输入量概率密度分布的影响，且为了获取更加可靠和稳定的评定结果，一般采用较大的执行次数。因此使用MCM可以获得更多的输出量信息，使得结果更精确。

为更直观对比GUM法和MCM的评定效果,对GUM法的评定结果，以最佳估计值为期望、标准不确定度为方差作概率密度分布图，以由MCM所提供的概率密度分布的离散数据作概率密度分布直方图，对比两个分布图的差异并验证GUM法是否通过MCM的验证。

4.1 输入量分布为正态分布

设定输入量即、、、、、的分布为正态分布。GUM法的概率密度分布图和MCM所得的概率分布直方图对比如图3所示，从表6可看出：输入量为正态分布时，单批次MCM和自适应MCM都与GUM法有较好的结果一致性，、均小于数值容差0.05，GUM法通过单批次MCM和自适应MCM的验证。

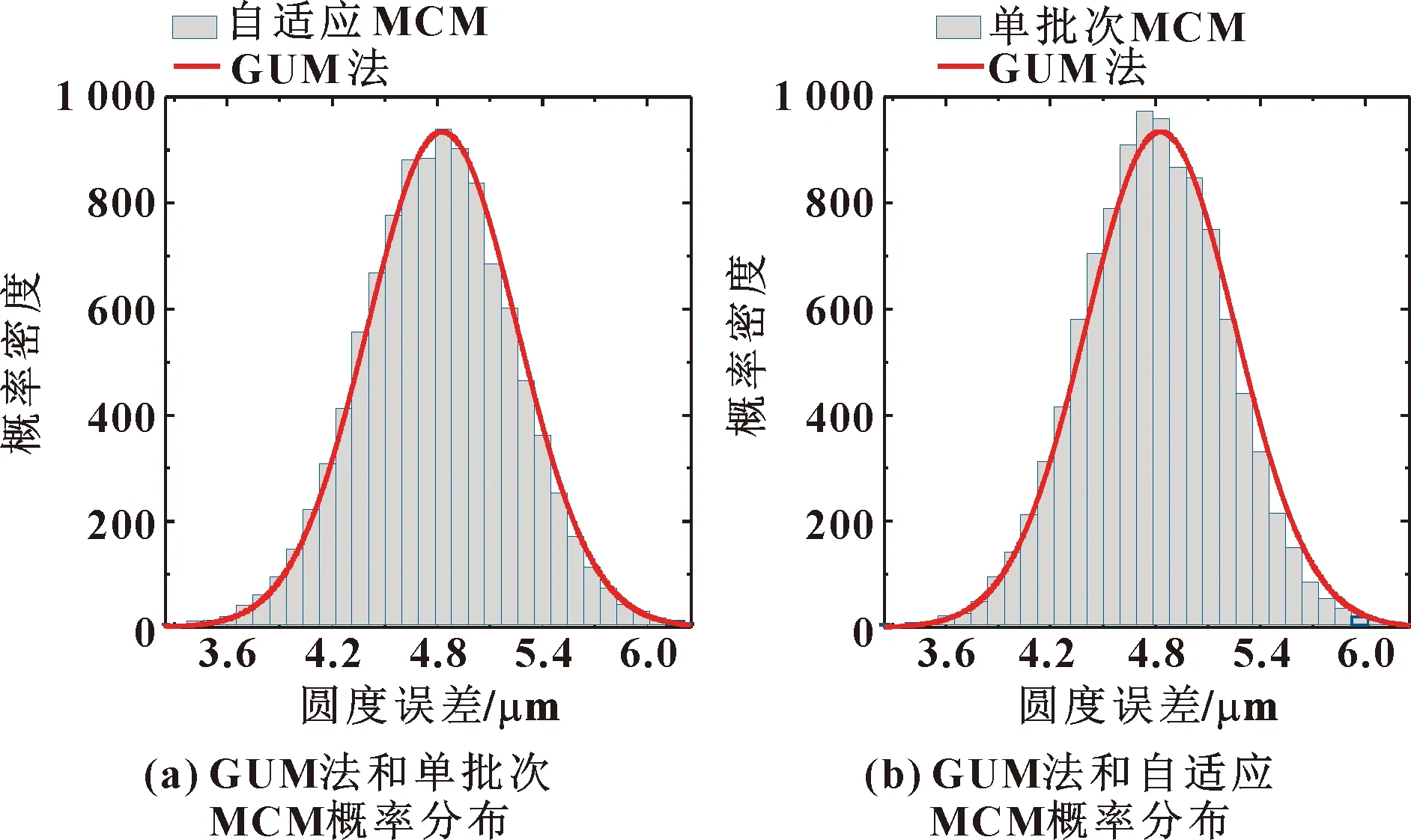
图3 GUM法和MCM的概率密度分布

表6 GUM法、MCM评定结果

4.2 输入量分布为非正态分布

因为将输入量设为正态分布，刚好满足了GUM法的评定条件，和MCM的评定结果有较好的匹配度。但在实际中无法将输入量假设为正态分布,此时输入量、、、、、可能且常见的分布有均匀分布、三角分布和梯形分布。改变输入量的概率分布类型，观察改变输入量分布的单批次MCM、自适应MCM和GUM法的结果对比，来探讨不满足GUM适用性的情况。同时观察GUM法是否可以通过MCM验证。方案及输入量分布类型如表7所示。方案一、二、三的GUM法和MCM的概率密度分布图分别如图4—图6所示，评定结果如表8—表10所示。

表7 输入量分布类型

由图4、表8可以看出：当输入量为均匀分布时，最佳估计值相差不大，但MCM的标准不确定度明显小于GUM法，且95%概率包含区间明显比GUM法更窄；、均大于数值容差0.05，GUM法没有通过单批次MCM和自适应MCM的验证。

表8 方案一GUM法、MCM评定结果

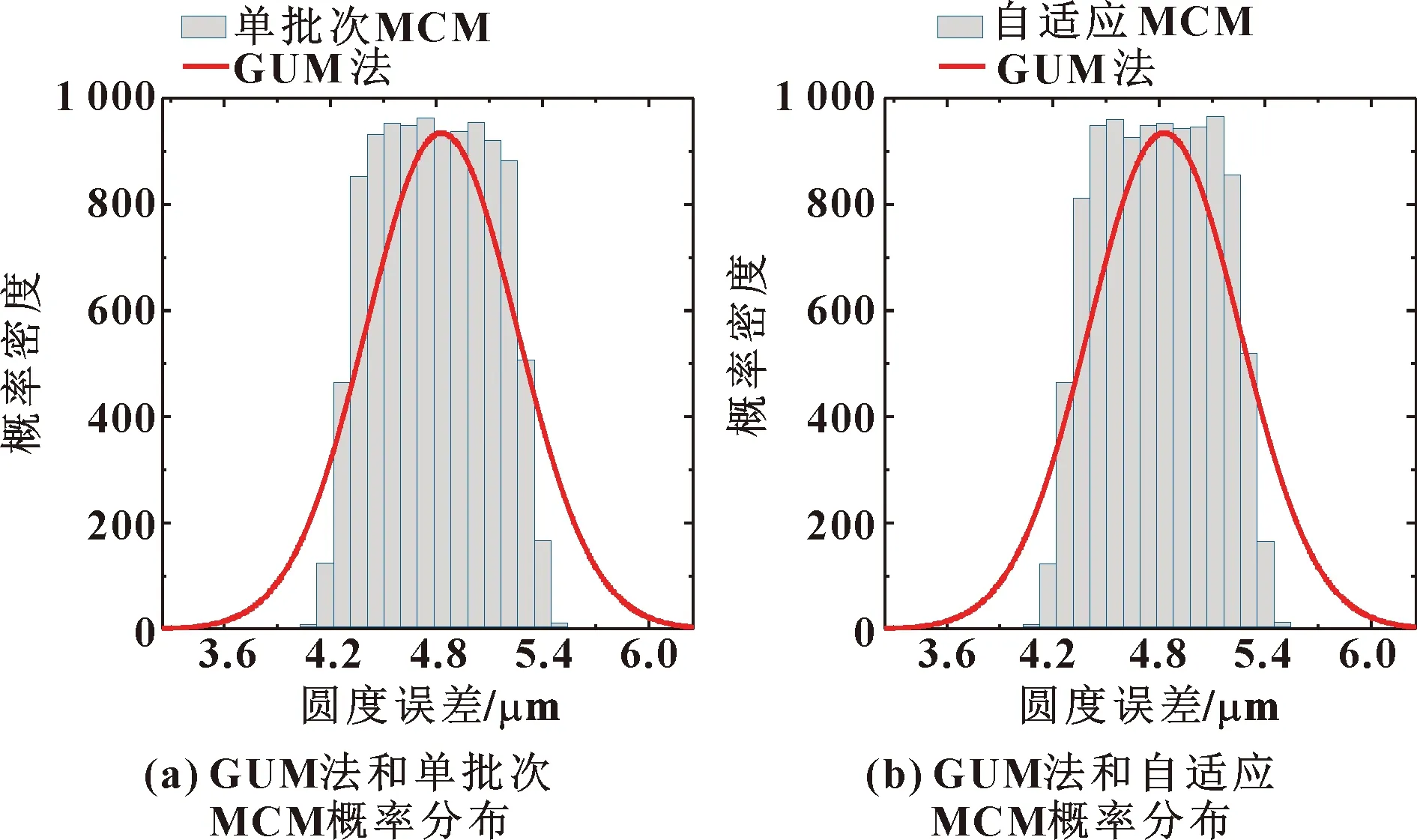
图4 方案一GUM法和MCM的概率密度分布

由图5、表9可以看出：当输入量为三角分布时，MCM的最佳估计值小于GUM法，MCM的标准不确定度小于GUM法，95%概率包含区间与GUM法差距不大但范围有明显偏离；、均大于数值容差0.05，GUM法没有通过单批次MCM和自适应MCM的验证。

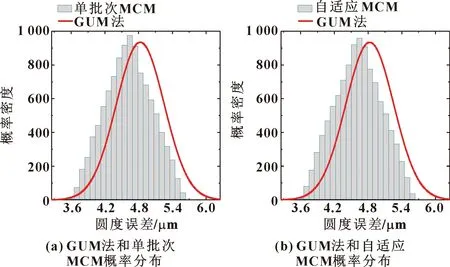
图5 方案二GUM法和MCM的概率密度分布

图6 方案三GUM法和MCM的概率密度分布

表9 方案二GUM法、MCM评定结果

表10 方案三GUM法、MCM评定结果

由图6、表10可以看出：当输入量为梯形分布时，MCM的最佳估计值明显小于GUM法，MCM的标准不确定度明显小于GUM法，95%概率包含区间明显比GUM法窄且范围有明显偏离；、均大于数值容差0.05，GUM法没有通过单批次MCM和自适应MCM的验证。

4.3 结果分析

通过输入量分布类型的改变可以看出：当输入量分布类型为正态分布即满足GUM法的条件时，GUM法与MCM得到的结果一致性好；当输入量分布为非正态分布时，由于GUM法采用近似的线性模型会忽略泰勒极值展开项，使得标准不确定度更大，95%概率包含区间更宽，结果就更保守；单批次MCM和自适应MCM的结果大体相同但有细微的差别，因为自适应MCM有稳定性判定等条件的约束，且计算机执行程序时会有一定的随机性，导致结果略有变化。

5 结论

为了正确而精准地评定轴承零件圆度，不仅需要评定圆度误差，还要给出其标准不确定度。GUM法和MCM都是目前计量领域主流的测量不确定度评定方法，本文作者使用这两种方法评定轴承零件圆度误差并进行对比分析，得出如下结论：

(1)输入量为正态分布时，GUM法和MCM的输出结果相近；当输入量为非正态分布时，MCM拥有更好的适应性，可以得到更精确的结果，GUM法未通过MCM验证，得出的结果较为保守，仅可用于误差不敏感场合，当对精度需求较高时，更建议使用MCM。

(2)MCM具有更贴近实际的模拟策略，且 MCM在评定测量不确定度时，表征了更多的输入量的分布信息，结果可信度高。且不需要繁复的求导计算，可操作性强。

(3)单批次 MCM 和自适应 MCM 评定测量不确定度的结果一致性较好，在进行测量不确定度评定时可自由选择。