全金属可溶桥塞异形接触结构密封特性*

崔 璐 邹 方 程嘉瑞 王 澎 李 臻 窦益华

(1.西安石油大学，西安市油气井完整性评价重点实验室 陕西西安 710065；2.蜂巢动力系统(江苏)有限公司 江苏扬中 212214)

多级分段压裂技术作为提高非常规油气采收率的有效方法，在完井领域技术成熟、应用广泛[1-2]。桥塞是分段压裂技术的核心组件之一，随着开采方向朝高温高压地层发展，常规桥塞采用胶筒作为密封组件，其密封性能难以满足要求，并且需要压裂作业后清理等工序。全金属可溶桥塞作为一种新型井下工具，采用可溶金属密封环与套管接触，可实现更有效的密封效果[3-4]。赵振峰等[5]自主设计了一种金属定位弹性球座，配合可溶球，并通过地面物模实验证明了密封的可靠性。刘腾等人[6]设计了一套全金属可溶桥塞，并对该桥塞的溶解性能、耐温承压进行了实验分析，发现在承压48 h后密封失效，但未解释其失效原因。陈振等人[7]采用数值模拟的方法对2种可溶材料进行对比分析，并对单凹槽密封环结构进行优化，确定最佳参数来满足密封性能。魏辽[8]通过粉末冶金的方法制备了石墨烯增强铝基可溶球座，并通过实验评价了球座的密封承压能力和溶解性能。李炎、于颖嘉、GOLTSBERG等[9-11]结合有限元法和实验证明了接触宽度仅对低载荷有影响，对于较高载荷，主要影响因素是最大接触压力和表面粗糙度。

相对于其他成熟的井下工具，全金属可溶桥塞作为较新型的井下工具，对密封性能评价尚没有成熟标准，目前主要参考封隔器、悬挂器等对金属密封的研究方法作为参考。李纯金等[12]设计了一种压缩扩张式的密封件，并用ABAQUS分析密封环宽度、承压环高度、膨胀半径、拱形半径、拱形厚度、卸载槽半径对弹性阶段接触应力的影响规律。WANG等[13]考虑C形环轴对称特性，将其分解为悬臂梁模型和简支梁模型，推导出了接触压力的理论模型，结合有限元模拟得到了最佳初始过盈量。田懿等人[14]建立了采油树K形密封环结构模型，并通过数值模拟分析了预压缩量、介质压力、温度对密封性能的影响，得出各参数的合理取值范围。YANG等[15]采用数值模拟和理论分析结合的方法，建立了井下K形金属密封接触应力与自变量之间的理论模型，结果表明解析解与数值解趋于一致。KIM等[16]针对O形金属密封圈，使用ANSYS软件来进行形状优化、结构改进以获得更好的回弹能力。崔晓杰等[17]利用有限元方法研究了外套管约束下的密封原理，并证明了金属密封技术针对于大间隙密封的可行性，但是没有揭示其密封机制。李玉婷等[18]利用ABAQUS软件建立了金属密封U形环的二维轴对称模型，但未研究U形环的结构参数对密封性能的影响。刘洋等人[19]基于椭圆密封结构设计理念，开发出一种锥形多曲面形大通径芯轴式套管悬挂器，并通过室内实验证明了该结构的可靠性。WALTON等[20]通过实验研究了可溶金属与可溶塑料制成的压裂堵头在压差作用下的瞄定性能。TAKAHASHI等[21]使用数值模拟与实验室压力测试技术研究了挤压可溶橡胶与套管之间的接触压力变化规律。

以上研究主要分析弹性阶段密封环变形特性，实际上全金属可溶桥塞在大间隙下的变形过程中同时发生塑性变形，其密封效果与密封环的结构形式强相关。为此，本文作者基于有限元法，探讨4种不同结构形式的金属密封环在锥体轴向位移量下的弹塑性变形、密封性能、不同表面粗糙度下von Mises应力分布等参数，系统讨论锥体轴向位移下4种模型的性能差异。

1 全金属可溶桥塞工作原理与密封准则

1.1 全金属可溶桥塞工作原理

全金属可溶桥塞的工作原理如图1所示。桥塞整体通过中心拉杆2与其他部件串联而成，在其底部通过螺纹与尾座7连接，通过释放螺纹的拉脱实现桥塞坐封和丢手。锥体1承受坐封工具推筒施加的坐封力，在坐封力的作用下锥体1沿轴向运动，同时锥体1是卡瓦基座4、变径密封环3的移动面，在锥体轴向推动作用下卡瓦牙6径向扩张咬入套管5实现锚定，变径密封环3与套管5挤压接触，从而实现井眼封堵[22-23]。

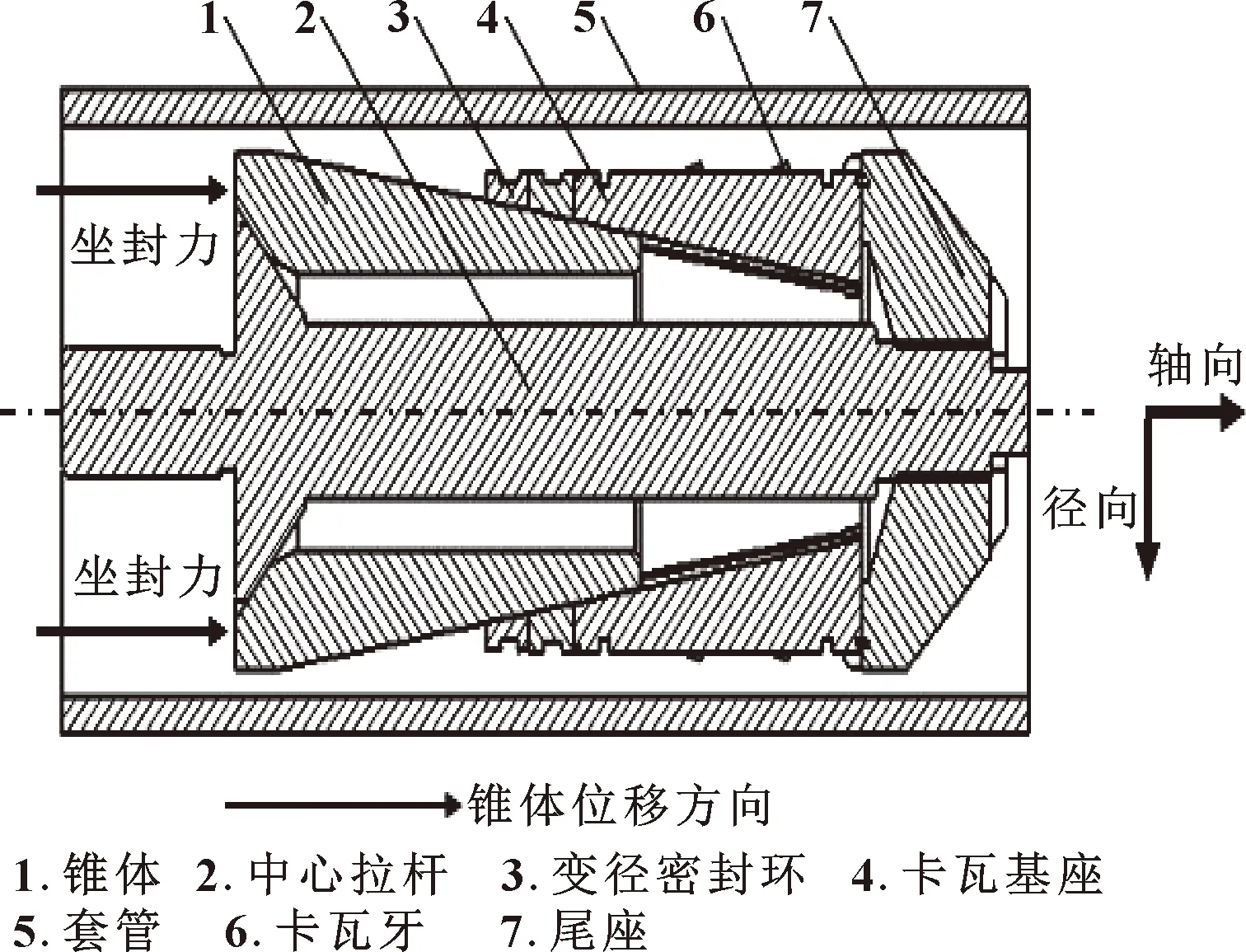
图1 全金属可溶桥塞工作原理示意Fig.1 Schematic of all-metal bridge plug

1.2 全金属可溶桥塞密封准则

目前对金属密封的研究，主要比较密封面间的接触压力与工作压力。文献[24-26]指出，在工作压力小于34.5 MPa时，接触压力大于工作压力与垫片系数乘积，能够实现密封；但是在工作压力大于34.5 MPa时，需使密封面的接触压力超过工作压力的3～10倍，总密封宽度在1.5～2 mm以上，才能实现有效密封，此判据是目前金属密封的最高准则。

2 全金属可溶桥塞金属密封性能分析

2.1 几何模型

为了简化计算，将全金属可溶桥塞核心的金属密封环与锥体套管组成的密封组件作为研究对象，同时对各部件受力分析做出如下假设：

(1)变径密封环为完全轴对称安装，无偏心。

(2)变径密封环与套管、锥体接触表面无缺陷。

(3)密封环、套管、锥体均视为各向同性连续体。

平台底层主要包括基础硬件、网络设备、系统软件等形成的网络支撑层和RFID技术、条码识别、传感器、智能手持等技术手段形成的信息感知层。

文中以单槽形(结构1)、椭圆形(结构2)、双槽形(结构3)、双曲形(结构4)4种结构形式的金属密封环为研究对象，研究坐封过程中的密封特性。图2给出了4种不同金属密封环的结构，表1给出各密封环主要结构参数。

表1 各密封环结构主要参数Table 1 Main parameters of each seal ring structures

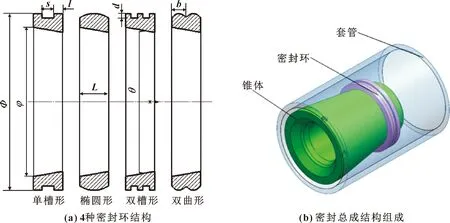
图2 不同密封环结构和密封总成结构组成示意Fig.2 Schematic of different seal ring structures and sealing assembly structure：(a)four kind of sealing ring structures：(b)structural composition of sealing assembly

2.2 材料参数

金属密封环、锥体选择不同类型可溶镁合金材料，套管选择P110钢，各部件材料参数如表2所示。

表2 各部件材料参数Table 2 Material parameters of each component

2.3 网格划分与边界条件

利用Workbench Mesh进行网格划分，其中密封环采用四面体网格划分，锥体和套管采用六面体网格划分，对接触面网格做加密处理。

定义金属密封环内周面与外锥体面、密封环外周面与套管内侧为摩擦接触，套管外侧固定约束。接触算法采用增强拉格朗日法，迭代采用完全牛顿拉普森法，密封环网格模型与边界条件如图3所示。

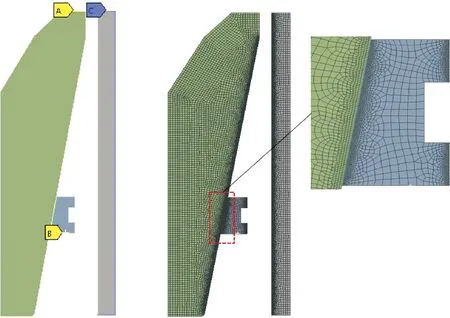
图3 密封环网格模型和边界条件Fig.3 Seal ring mesh model and boundary conditions

2.4 网格无关性验证

在单槽形密封环坐封条件下，选取不同网格数量的模型开展了全金属可溶桥塞金属密封计算域的网格无关性验证，结果如图4所示。可以看出，在网格数量由3万变化至50.4万过程中，密封环与套管接触应力变化幅度趋于定值，且当网格数量为25万时，接触应力开始趋于一致，网格数量继续增加到50.4万时，接触应力的数据基本保持不变。针对密封环径向变形而言，在网格数量从16万到50.4万时，径向变形值保持不变。综合考虑计算效率和计算精度，选取38万网格数量开展后续模拟研究。

图4 接触应力和径向变形随网格数的变化Fig.4 Variation of contact stress and radial deformation with the number of grids

3 结果与讨论

3.1 不同结构密封环径向变形特征

密封环的径向变形程度决定了接触面间的密封性能，通过模拟锥体推送过程中密封环的径向变形，为研究坐封过程密封特性提供理论基础。

4种不同结构密封环的径向变形曲线如图5所示，以初始位置为坐标零点，随着锥体向右移动直至坐封完成，4种密封环结构径向变形一致呈现出阶段性线性增长的规律。然而4种密封环结构变形量虽均随锥体轴向位移量增大，但最终变化幅值存在较大差异，曲线形(椭圆形和双曲形)结构密封环在扩张过程中始终大于凹槽形(单槽形和双槽形)结构密封环。从轴向位移量63.4～64.5 mm间放大图可以明显看出，在位移点64.07 mm前，4种结构的变形维持等差量，但在该位移点后，相比曲线形结构，凹槽形结构密封环的变形速率下降明显。这是因为针对于弹塑性分析结构的整体刚度始终属于变值，加之接触非线性因素，接触后也相应限制了变形，导致应变能积累，各结构抵抗变形能力不同。由此可推断4种结构在初始接触时锥体轴向位移量为64.07 mm。在同样的锥体轴向位移量64.5 mm下，4种结构中椭圆形结构的径向变形量最大，为10.435 mm，双曲形结构次之，为10.412 mm，单槽形结构最小，为10.135 mm。但椭圆形结构的变形值只是略高于其他3种结构，最大相差仅为0.47%

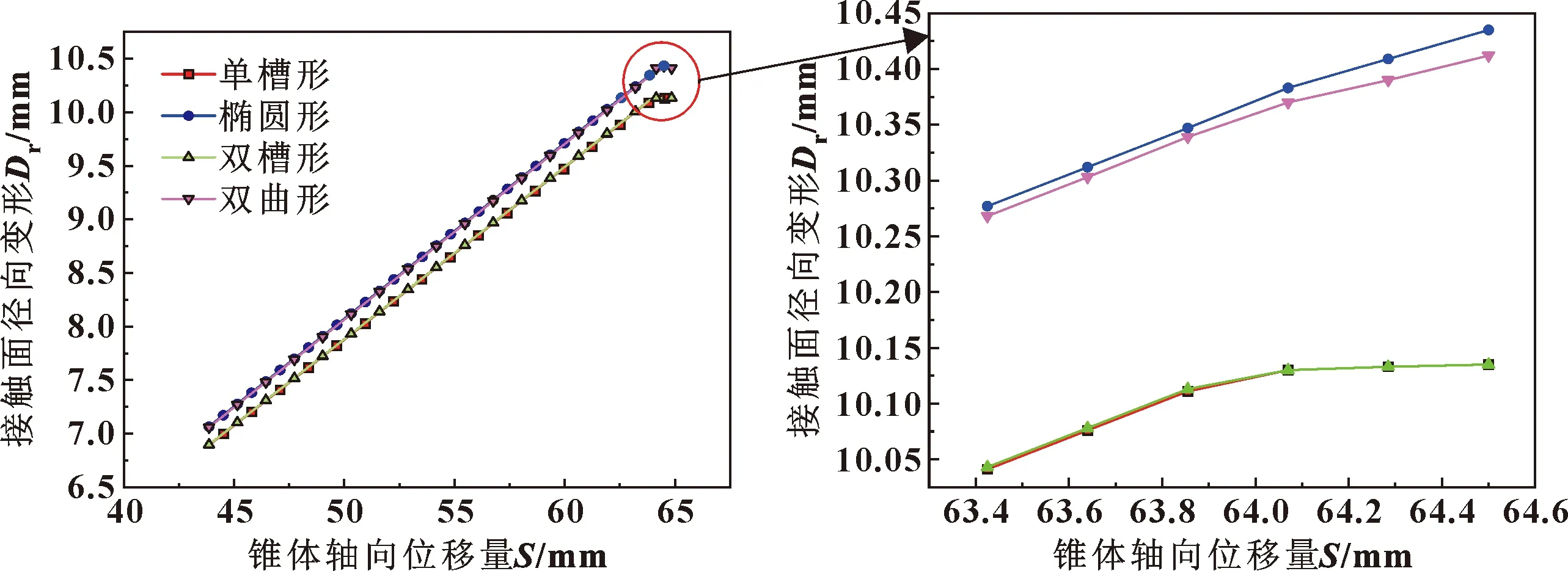
图5 不同结构密封环在不同锥体轴向位移下的径向变形Fig.5 Radial deformation of sealing rings with different structures at different axial displacement of cone

选取双槽形和双曲形2种结构分别代表曲线形和凹槽形两对照组，分析2种结构接触面径向变形随锥体轴向位移量变化过程，结果如图6所示。密封面的最大变形量都发生于密封环厚度最大的外圆侧，说明密封环的变形过程整体趋势为厚度大的一侧高于厚度小的一侧。由此得出，在变形接触过程中，对于凹槽形结构，其厚度较大的一侧先与套管接触形成密封；而对于曲线形结构，虽然最大外圆周变形程度大于凸体变形，但是从图6(b)可知，接触过程中总是凸体与套管先接触，针对双曲结构，变形过程中右侧凸起变形程度大于左侧凸起，右侧先行接触。

图6 接触面径向变形随锥体轴向位移量的变化过程Fig.6 The process of radial deformation of contact surface with the axial displacement of cone：(a)radial deformation process of double groove structure；(b)radial deformation process of hyperbolic structure

结合图5和图6中结果，可得到结论：对于密封环整体径向变形和接触面径向变形，凸曲线形结构变形特性始终优于凹槽形结构，椭圆形结构变形量最大，双曲形结构次之，单槽形结构最小。

3.2 不同结构密封环密封特性分析

设定金属密封环接触面锥度为10°，工作温度为20 ℃，介质压力为70 MPa，研究了4种密封环结构在锥体轴向位移量43.00～64.50 mm下的性能变化。

图7所示为不同结构密封环von Mises应力云图，可见最大von Mises应力发生位置均位于密封环与锥体的接触面。这是由于密封环与锥体接触特殊的尖角结构导致其刚度较小，导致在膨胀过程中容易产生大的von Mises应力。

图7 不同结构密封环应力云图Fig.7 Stress cloud diagram of sealing rings with different structures

在完成坐封后，4种密封环最大von Mises应力均大于抗拉强度210 MPa，最大应力点最有可能成为损伤点位。由图7可以看出，与单槽形和双槽形结构相比，椭圆形结构的损伤位点更密集，几乎遍布整个密封环内周面，双曲形结构应力集中程度有所减缓。同时，4种密封环结构全部发生塑性流动，能够形成有效的密封。

图8示出了4种金属密封环接触应力、接触面积、塑性应变、锥体坐封反力随锥体轴向位移量的变化情况。可以看出，随着锥体轴向位移量由43.0 mm增加到64.50 mm，接触应力、接触面积、塑性应变、支反力均不断增加，分别由初始零状态增加至312.48 MPa、2 109.96 mm2、0.180 0 mm、186 kN(单槽形)；464.11 MPa、475.83 mm2、0.192 7 mm、121 kN(椭圆形)；329.05 MPa、2 143.53 mm2、0.178 0 mm、191 kN(双槽形)；550.01 MPa、598.16 mm2、0.195 6 mm、138 kN(双曲形)。这是因为锥体轴向位移量的大小决定了密封环与套管的接触特性，从而决定了结构的密封性能。

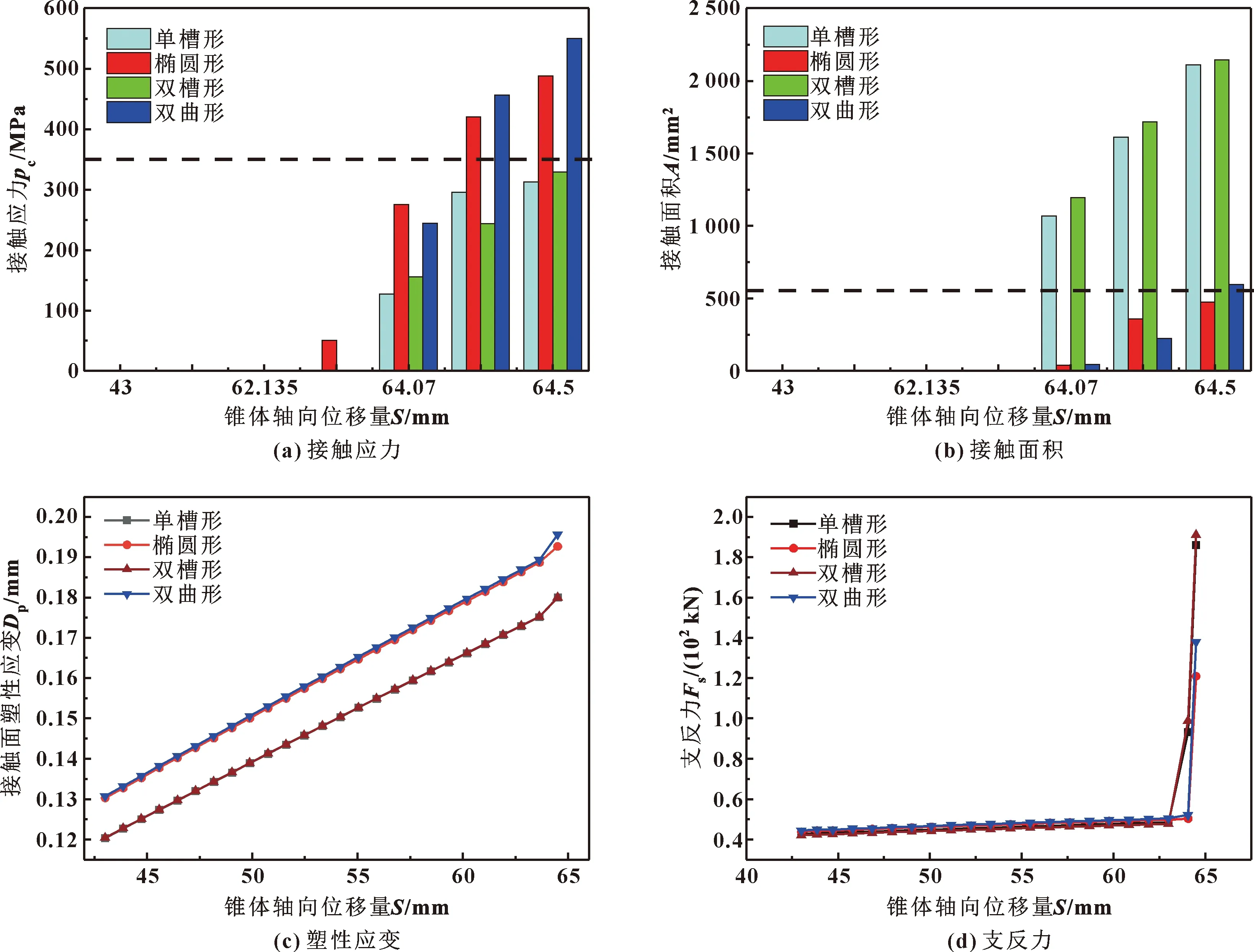
图8 密封参数随锥体轴向位移量变化曲线Fig.8 Variation curves of sealing parameters with the axial displacement of the cone：(a)contact stress；(b)contact area；(c)plastic strain；(d)support force

从图8(a)和图8(b)可以发现，椭圆形结构在锥体轴向位移量为63.855 mm时首先与套管接触，在锥体轴向位移量为64.07 mm时，4种结构都已经发生接触；在整个坐封过程中，凹槽形结构的接触面积始终大于曲线形结构，而接触应力却相反，这是因为在接触过程中，凹槽形结构相当于圆柱面与圆柱面内切，而曲线形结构相当于椭球面与圆柱面内切。如图8(c)所示，锥体轴向位移量越大，一定程度上密封环接触面发生塑性应变程度越大，与套管贴合就越紧密；在整个坐封过程中曲线形结构塑性应变始终大于凹槽形结构，在相同锥体轴向位移量64.50 mm下，双曲形结构塑性应变最大。支反力随锥体轴向位移量的变化曲线如图8(d)所示，在密封环与套管接触前坐封力几乎没有任何差别，但在接触后会导致坐封力激增，凹槽形结构坐封力几乎是曲线形结构坐封力的1.5倍。但是锥体轴向位移量过大会引起密封环的强度破坏，文献[7]也得出相似的结论。

根据井下的实际情况，文中选取接触压力大于工作压力5倍、密封接触宽度1.5 mm作为判断依据。4种密封环结构在相同锥体轴向位移量64.5 mm下，各因变参量存在不同，对于接触应力密封准则，椭圆形和双曲形结构满足要求，但是对于接触宽度密封准则，椭圆形结构并不能满足要求。结合图7和图8可知，双曲形结构密封性能最高，双槽形结构次之，椭圆形结构最差，这是因为在弹塑性分析中，椭圆形模型结构复杂，曲面结构增加了密封环与套管初始接触时的接触面积，又改变了结构接触后产生的应变能。

3.3 密封环表面粗糙度对密封性能的影响

由前文分析可以得到结论，在所述4种密封环结构中，双曲形结构变形能力、密封性能优于其他3种结构。实际接触情况下，考虑接触面的粗糙程度更能反应真实情况，为此，探讨了在实际情况下不同摩擦因数时双曲形结构的接触性能[27]。

图9所示为双曲形密封环接触面接触应力、接触面积随摩擦因数变化曲线。随着摩擦因数的增大接触应力呈线性增大规律，当摩擦因数从0增大到0.3时，接触应力从542 MPa增大到552 MPa。然而随着摩擦因数增大，接触面积却从599.05 mm2下降至597.55 mm2，这是因为施加摩擦因数，相当于考虑了切向力的影响，在同样锥体轴向位移量下，切向力越大，对接触过程中密封环变形阻力越大。

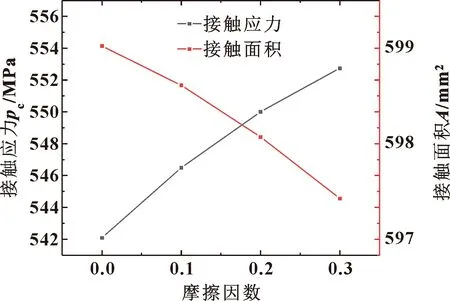
图9 密封性能随摩擦因数变化Fig.9 Variation of seal performance with friction coefficient

不同摩擦因数下密封环的应力分布如图10所示。由图10(a)可知，随着摩擦因数的增大，在密封环内表面应力集中程度不同，摩擦因数升至0.2时，内表面应力集中程度突扩至较薄一侧，并且随着摩擦因数继续增加至0.3，应力集中程度占比达到50%以上。由图10(b)可知，切向摩擦会导致双曲形密封环凸体顶部的等效应力略有增加，无摩擦接触时，相比较而言局部应力集中程度不明显，最小应力点在远离接触点位置，随着摩擦因数增大，应力集中区域逐渐向摩擦力方向偏移，摩擦因数增加为0.3时，对凸体顶部等效应力影响最大，应力云图向初始接触点偏移增大，且形状不完整。结合图9和图10可得，在摩擦因数取值0.18左右双曲形密封环性能最优，这是因为在该摩擦因数下密封环内表面应力集中程度较小、凸体顶部应力分布更加均匀。

图10 不同摩擦因数下密封环Mises应力分布Fig.10 Mises stress distribution of seal rings at different friction coefficients：(a)effect of friction coefficient on Mises stress of inner wall surface；(b)effect of friction coefficient on Mises stress of top of convex body

4 结论

设计了4种不同结构的金属密封环，在所研究参数值范围内利用Workbench模拟研究了在相同锥体轴向位移量条件下4种密封环的径向变形特征、密封性能、应力分布，并对比有无切向力对双曲结构密封环性能的影响，结论如下：

(1)4种结构密封环径向变形规律基本一致，径向变形过程中壁厚较大一侧变形量始终大于壁厚较小一侧，曲线形结构变形量始终大于凹槽形结构，并且在接触后凹槽形结构变形速率下降更加明显。

(2)4种密封环在径向变形过程中接触应力、接触面积、接触面塑性应变、支反力均逐渐增大，其最大损伤点均位于密封环内壁面。对于接触应力密封准则只有椭圆形和双曲形结构满足要求，而对于接触宽度密封准则只有双曲形结构满足标准。

(3)双曲形结构密封性能最高，考虑切向力会导致该结构接触应力增大，接触面积减小；同时增大摩擦因数会使金属密封环凸体顶部von Mises应力集中分布发生变化。