基于角谱域和时间反演的任意均匀场的生成方法*

安腾远 丁霄

(电子科技大学应用物理研究所,成都 611731)

现有均匀场往往基于阵列天线的特殊排布,通过平顶波束赋形在角远场区域或者通过点聚焦在近场区域生成的,生成的均匀场直接受制于阵列排布形态且无法灵活调控.提出了一种基于角谱域和改进时间反演方法相结合的均匀场生成方法,该方法不受阵列排布的限制,能够以同一阵列排布形态,在包括近场区域在内的任意位置,生成指定大小、形状以及偏转角度的多种均匀场.首先理论解析了本方法不受阵列排布限制的原因;其次数值验证了固定阵列排布形态灵活生成多种均匀场的能力;最后引入时间反演方法,并做出反演信号幅度倒数加权的改进,解决了上述均匀场在生成过程中由幅度衰减和相位延迟带来均匀场平坦度恶化等问题.研究结果表明,合成场质量与其对应角谱域包络的主瓣和副瓣信息有关,且生成任意均匀场必须包含至少1/2 的角谱域主瓣信息和1/2 的副瓣信息.本方法能够灵活调控一维和二维均匀场的位置、大小、形状以及偏转角度,为灵活生成均匀场提供了一条新思路.

1 引言

均匀微波场通常指目标区域内的微波场具有均匀的场强分布,其在空中测试(OTA)[1]、微波热成像[2]、微波加热[3,4]以及射频识别(RFID)[5]等应用领域发挥着重要作用.先前,研究者们提出了多种均匀微波场的合成方法,如伍德沃德-劳森抽样合成法[6]、泰勒方法[7]、艾里奥特合成法[8]以及矩阵铅笔法[9-11].伍德沃德-劳森抽样合成法相对简单,但通过此方法分析得到的均匀场波束具有较高的副瓣,且目标区域的抖动波纹较大.相比之下,泰勒方法、艾里奥特合成法以及矩阵铅笔法在副瓣和目标区域均有良好的表现,但是生成的均匀场仍然受限于天线阵列的排布,无法灵活地改变目标场的位置以及形状.最近又出现了通过计算机迭代优化的均匀场赋形方法[12-15],一方面,这些方法既能够抑制旁瓣电平,在一定程度上又能够控制目标场的位置以及形状.但是这些全局优化方法计算量往往随着阵列规模和场形复杂度的增加而增加.另一方面,上述提及的合成均匀场的方法大多是基于天线阵列的角远场区域,通过生成平顶波束从而获得的.但是随着电磁应用环境日益复杂,往往要求固定排布形态的天线阵列具备生成多种均匀场的潜能,如微波加热系统以及肿瘤探测就要求在笛卡儿坐标系下的近场区域内生成任意可调的均匀微波场[16,17].因此,亟需一种能够在阵列近场区域内,灵活调节均匀场的场型以及位置的方法.

时间反演方法以其灵活快速的波束调控和场赋形能力而备受关注[18-22].文献[19]中提出了利用时间反演多点聚焦的方法,在指定位置通过多个聚焦斑线性叠加,生成任意规定图案的电场.但是该方法产生的目标场的波纹抖动受到各个聚焦斑的大小和位置的影响,且单纯的时间反演方法严重依赖多径效应,限制了其应用场景.文献[23]提出了一种基于角谱投影和线性叠加的场整形方法,通过将目标场的空间域变换为角谱域,借助“伞形”、“半圆形”排布的阵列,通过不同入射角的投影线性叠加生成指定的目标场.文献[24]在文献[23]的基础上,首次提出利用空间角谱投影和时间反演方法相结合的方法产生阵列对应圆心位置处的均匀场,但是仍受阵列排布的影响无法实现灵活可调的效果,且文献中时间反演的作用只是为了解决单元耦合、缺失以及阵元出现偏移带来的影响.

据此,本文利用角谱域变换并结合时间反演方法,基于固定形态的线阵和均匀栅格平面阵,提出了一种灵活调控均匀场位置、大小、形状以及偏转角度的通用方法.该方法不需要计算机迭代优化,通过合理的空间域与角谱域的傅里叶变换和快速的时间反演,即可确定阵列中每个阵元的幅度和相位,从而得到所需的均匀场.多种数值计算验证论证了该方法的有效性和可靠性.

2 基于角谱域的任意均匀场合成方法

类似于通信领域中的信号,可以通过傅里叶变换在时域和频域相互转变.对于空域中一个已知空间分布的任意场型,也可以通过傅里叶变换转换为角谱域形式,如一个矩形脉冲信号可以转换为不同频率的信号的叠加.因此,按需生成空间分布的任意场型,可转换为求解不同角频率信号的相互叠加.

2.1 一维均匀场的合成

一维均匀场的数学模型可以用矩形窗函数表示.假设在x轴上有宽度为τ的均匀场,该均匀场可表示为

其中A表示该均匀场的幅度.对Eumf进行傅里叶变换,将其变换为角谱域形式,即

其中,kx表示x方向的空间角频率(空间波数),sinc(·)是辛格函数.可以看出一维均匀场的角谱域形式是一个与均匀场宽度τ相关的辛格函数.在自由空间中当|kx| >k0时,即x方向的空间波数kx大于自由空间波数k0,此时的电磁波为倏逝波,其幅度随着距离的变化呈指数衰减无法远距离传播.因此在自由空间中一维均匀场可以看作由角频率为|kx| ≤k0的场组合而成,即

式中,k0=2π/λ为自由空间波数,其中λ表示为任意频率电磁波的波长.对于均匀微波场数学上可以看作从-k0–+k0无数个连续的角频率场的叠加,但是现实中无法实现连续叠加.因此对于由阵列产生的均匀场,可以将其对应的角谱域离散化处理.其中由N个阵元组成的天线阵列,第n个阵元在均匀场的位置对应的角频率kxn为

其中,θn为第n个天线相对于均匀场中心的夹角.因此可以通过抽样函数将(3)式离散化处理,那么对应角频率叠加而产生的合成场为

其中δ(·)表示冲激函数.通过(4)式和(5)式可以看出,不同的阵列排布产生不同的采样函数,而不同的采样函数影响最终合成电场的平坦度.此处,采用等空域划分的半圆阵列以及等空域划分的直线阵列,与文献[23,24]中提出的等角谱域划分的半圆阵列进行分析比较,来证明采用等空域划分的直线阵列的可行性.

首先设置均匀微波场位于x轴中心位置,宽度为4λ.半圆阵列半径为10λ,直线阵列中心位置距离均匀场中心位置10λ,阵元间距0.5λ,其中λ为任意值.3 个阵列均由31 个阵元组成,其具体模型如图1 所示.

图1 三种不同的阵列排布方式Fig.1.Three different array arrangements.

3 种不同的阵列排布对应3 种不同的抽样方式,作用于宽度为4λ的均匀场角谱域,各个角频率对应的幅度如图2(a)所示.可以看出等角谱域半圆阵列在-k0–+k0的范围内均匀采样,等空域直线阵列采样点主要集中在主瓣附近,而等空域半圆阵列采样点主瓣附近较少,主要集中在两侧.将采样结果代入(5)式并观察目标场合成效果,其合成结果如图2(b)所示.

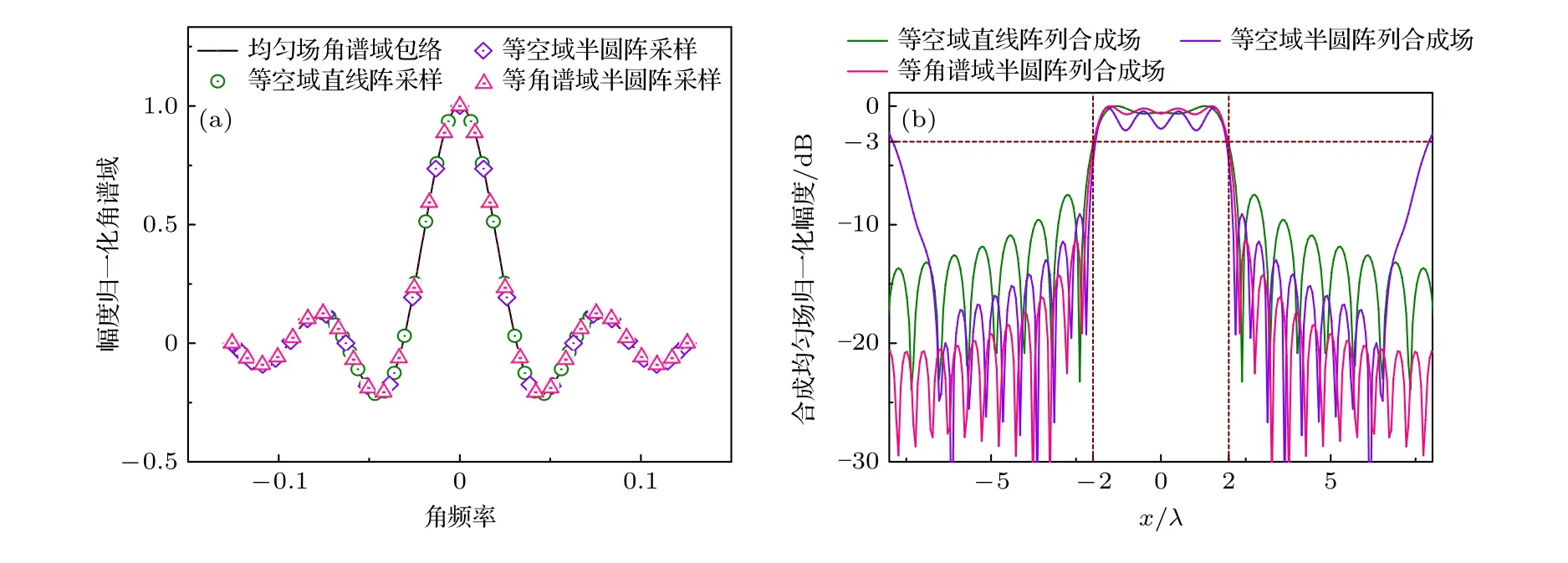
图2 三种不同阵列排布对应的角谱域采样图和合成场分布图 (a)归一化角谱域采样图;(b)归一化电场分布图Fig.2.Angular spectrum domain sampling diagram and synthetic field distribution diagram of three different array configurations:(a) Normalized angular spectrum domain sampling diagram;(b) normalized electric field distribution diagram.

从图2(b)可以看出,3 个合成场在-2λ–+2λ的范围内合成场的幅度保持在-3dB以上,在±2.5λ附近出现大小在-20dB左右的第一零点,场型具有较好的滚降,说明3 种阵列排布均能实现在目标区域生成指定大小的均匀场.因此完全可以采用简单的等空域直线阵列代替复杂且占用大量空间的半圆阵列,去生成均匀微波场.

由吉布斯现象可知,当合成矩形脉冲波形时,选取有限项项数越多,合成波形质量越好越接近理想的矩形脉冲.结合上述分析算可以看出当选取项数相同时,角谱域主瓣采样点越多,合成场主瓣波纹越小,越趋于一个固定数值;反之主瓣波纹越大.换言之,均匀场的主要信息集中在其对应的角谱域主瓣内,相同规模的等空域直线阵列可以产生更平稳的均匀微波场.

当生成同一目标均匀场时,对于不同规模相同阵元间距的等空域直线阵列,角谱域信息的差别主要体现在副瓣上.因此保持目标均匀场仍在阵列轴线上,目标均匀场位于阵列10λ处,阵元间距0.5λ不变,改变阵元数量.对应角谱域和合成场如图3所示.

图3 改变阵元数量后的角谱域和合成场 (a)阵元间距为0.5λ 的角谱域采样结果;(b)不同阵元数量的阵列在目标位置的合成场Fig.3.Angular spectrum domain and generated field after changing number of array elements: (a) Angular spectrum domain sampling results with a spacing of 0.5λ between array elements;(b) composite field of arrays with different number of array elements at target position.

本文选取了4 种不同阵元数量的阵列,其中当阵元数量为11 个时,其角谱域只包含对应角谱域包络的主瓣;当阵元数量为17 个时,其对应角谱域包含对应角谱域包络的主瓣和1/2 个第一副瓣.通过合成场对比可以发现,当角谱域信息只包含全部主瓣,缺少副瓣信息时,合成场在±2λ的位置幅度明显小于-3dB,平坦度较差,无法正常生成目标均匀场.当角谱域信息包含主瓣和1/2 副瓣时,合成场在±2λ的位置幅度在-3dB左右,合成场主瓣平坦度较好,并且随着角谱域中副瓣信息的增多,滚降系数增大,但是当角谱域主瓣采样点数量比副瓣采样点数量小于1/2 时,合成场主瓣波动剧烈,合成场质量恶化.因此通过等空域直线阵列合成均匀场时,不但需要角谱域主瓣信息,还需要足够数量的角谱域副瓣信息,至少要包含1/2 角谱域副瓣信息.

为了进一步探究等空域直线阵列灵活调控均匀场的能力,利用非均匀直线阵列和等空域直线阵列进行对比分析,非均匀直线阵列与等空域直线阵列口径相同,第1–7 个单元以及第25–31 个单元间距0.7λ,第8–24 个单元间距0.3λ.并且保持相对距离10λ、相对宽度4λ不变,改变均匀场在x轴上的位置,两阵列的排布如图4(a)和图4(b)所示.图5展示了当目标均匀场中心位置位于x轴(0λ,0),(+6λ,0)以及(-8.5λ,0)处两阵列的角谱域采样结果以及合成场结果.

图4 两阵列和目标均匀场的空间分布 (a)等空域直线阵列 (b)非均匀直线阵列Fig.4.Spatial distribution of two arrays and target uniform field: (a) Isospatial linear array;(b) non-uniform linear array.

图5 目标均匀场对应的角谱域采样图和合成场分布图 (a)等空域直线阵列归一化角谱域采样图;(b)等空域直线阵列归一化电场分布图;(c)非均匀直线阵列归一化角谱域采样图;(d)非均匀直线阵列归一化电场分布图Fig.5.Angular spectrum domain sampling diagram and composite field distribution diagram of uniform field: (a) Normalized angular spectrum domain sampling diagram for isospatial linear array;(b) normalized electric field distribution diagram for isospatial linear array;(c) normalized angular spectrum domain sampling diagram for non-uniform linear array;(d) normalized electric field distribution diagram for non-uniform linear array.

为了方便突出3 个合成场场型的区别,在图5(b)和图5(d)中将3 个合成场的中轴线对齐.对比图5(a)和图5(b)可看出,随着均匀场位置偏离阵列轴线时,均匀场角谱域对应的辛格函数主瓣采样点减少,合成场场型恶化.尤其是当目标均匀场中心位于(-8.5λ,0),此时主瓣采样信息严重缺失不足1/2,已无法正常合成均匀场.虽然当目标均匀场偏离阵列轴线后的场型恶化,但通过分析(5)式可得,理想情况下其合成场仍然呈对称状态.对比图5(a)和图5(c)可看出,由于阵列的非均匀排布,当目标均匀场正对的区域阵元较多时,均匀场角谱域包络主瓣会有更多的角频率采样点,反之更少.从图5(d)可看出,非均匀阵列相较于均匀直线阵列在(0λ,0)的角谱域主瓣采样点更多,生成场质量更好;但是在(6λ,0)和(-8.5λ,0)的角谱域主瓣采样点更少,生成场波动更加严重,质量相对更差.因此虽然非均匀阵列在阵元密集对应的区域生成的均匀场质量更好,但是其灵活可调范围大大缩小.

根据上述分析可以得出如下结论:

1)当期望的均匀场未在阵列轴线上时,只要均匀场对应的角谱域主瓣有足够多的采样点,即可通过该阵列合成指定的均匀场;

2)当阵列对应的角谱域信息包含至少1/2 的角谱域主瓣信息以及1/2 角谱域第一副瓣信息时才能正常生成均匀场;

3)对于非均匀直线阵列,在阵元密集对应的区域合成的均匀场质量更好,在较稀疏的区域合成的均匀场质量相对较差;

4)在角谱域主瓣信息不严重丢失的前提下,利用等空域直线阵列可以更加灵活地调控均匀场.

2.2 二维均匀场的合成

在三维空间中生成二维平面均匀场,对空域进行傅里叶变换转变为角谱域时,需要同时考虑x和y两个方向的角谱分量,因此需要对空域做二维傅里叶变换.假设在xOy平面上有边长为τ的正方形均匀场,可以用下式表示:

对Eumf(x,y)关于kx和ky两个分量同时做傅里叶变换,将二维均匀场的空域形式转变为角谱域的形式,即

与2.1 节分析相同,考虑到微波在自由空间传播时波数的限制,在自由空间中二维均匀场可以看作由角频率满足的场组合而成,即

对于由N个阵元组成的阵列天线产生的均匀场,第n个阵元在目标区域对应的角频率kxn和kyn分别为

其中,θn为阵元指向目标场中心的射线关于z轴正半轴的夹角,φn为该射线在xOy平面内的投影关于x轴正半轴的夹角.最终由阵列天线离散抽样合成的场可以表示为

与二维空间生成一维均匀场相似,生成二维均匀场的阵列不需要拘泥于以满足角频率从-k0–+k0的均匀或非均匀采样而设计的特殊外形.本文采用均匀栅格平面阵,对二维均匀场的角谱进行离散采样,通过观察不同位置合成场的场型,分析均匀栅格平面阵对二维均匀场的调控能力.

在这里设置一个位于xOy平面、边长为2λ的均匀场.在距离xOy平面上方10λ处平行放置规模为21×21、阵元间距为0.5λ的阵列.由2.1 节分析可知,均匀场的信息主要集中在其对应的角谱域主瓣内,因此令目标均匀场的位置分别为(0λ,0λ),(0λ,-5λ)以及(-5λ,-5λ),来观测二维均匀场角谱域主瓣信息缺失程度对二维合成场的影响.每个阵元对应的归一化角频率如图6 所示,其中每个色块表示合成目标均匀场时,需要阵列提供的角频率的大小.

图6 各个阵元对应的归一化角频率 (a)目标均匀场位于(0λ,0λ);(b) 目标均匀场位于(0λ,-5λ);(c) 目标均匀场位于(-5λ,-5λ)Fig.6.Normalized angular frequency corresponding to each array element: (a) Target uniform field is located at (0λ,0λ);(b) target uniform field is located at (0λ,-5λ);(c) target uniform field is located at (-5λ,-5λ).

可以看出,图6(a),(b)和(c)分别具有(a)完整的角谱域主瓣,(b)1/2 的角谱域主瓣,(c)1/4 的角谱域主瓣.将每个阵元对应的角频率代入(10)式,求出由该阵列产生的合成场.为了直观展示合成场的区别,在图7 中将合成场幅度归一化并居中绘图.

图7 幅度归一化合成场 (a)目标均匀场位于(0λ,0λ);(b) 目标均匀场位于(0λ,-5λ);(c) 目标均匀场位于(-5λ,-5λ)Fig.7.Amplitude normalization field: (a) Target uniform field is located at (0λ,0λ);(b) target uniform field is located at (0λ,-5λ);(c) target uniform field is located at (-5λ,-5λ).

结合图6 和图7 可以看出,当采样点包含整个角谱域主瓣时,合成场中心区域幅度保持一致,在±1λ的位置附近出现低于-20 dB 的第一零点,可视为完美的正方形均匀场.但随着主瓣信息的缺失,合成场场型恶化.特别地,当目标均匀场位于(-5λ,-5λ)时,有3/4 的角谱域主瓣信息缺失,合成场中心凹陷,幅度小于-3 dB,边界处出现较大的波纹,已经无法被视为均匀微波场.因此对于二维均匀场,当均匀栅格平面阵包含的均匀场角谱域主瓣信息大于1/4 时,阵列可以灵活的产生均匀微波场,同时主瓣信息越丰富均匀场质量越卓越.

3 基于时间反演的阵元幅度相位优化方法

改用直线或平面阵列既可以灵活地调控均匀场,又大大缩小了阵列规模,但会导致不同阵元到达目标场的距离不同.如果不对各个阵元的幅度相位做进一步优化,那么不同角频率的波到达目标区域时幅度比例发生变化,初始相位不再相同,导致均匀场无法正常的合成.而所需要的幅度相位优化方案可以通过时间反演的方法快速获取[18].

时间反演空时同步聚焦特性可以快速补偿由于传播和耦合带来的相位差.对于传统的时间反演方法是按照幅度不变、相位共轭对信号进行处理的,这些信号再沿着原先路径反向传播,幅度再一次衰减,实则并没有解决第2 节忽略路径影响所产生的幅度优化问题,但是有关传播衰减和耦合的信息是包含在各阵元接收信号的幅度中.受到角谱域主瓣采样数量的限制,均匀场可调节范围在阵列天线的上方,所以阵元间的耦合较弱可以忽略.因此可在不考虑耦合对幅度造成影响的前提下,对传统的时间反演做出简单的变形处理,改进的时间反演具体步骤为:

1) 在目标均匀场中心放置探测天线并发射探测信号,记录各阵元接收到的探测信号.

2) 对记录的探测信号做时间反转,并提取时间反转信号对应的幅度an和相位fn.

3) 各个阵元的幅度在对应角频率大小的基础上,乘以时间反转信号对应幅度的倒数1/an,各个阵元的相位为时间反转信号的相位fn.

即可以通过一次时间反演获得的相位信息确定均匀场的中心位置,幅度信息来预处理各个角谱域分量在空间中的变化,最终实现对均匀场的灵活快速调控.

为了证明对时间反演方法改变的合理性,并详细展示各阵元基于改进时间反演所获取的幅度和相位信息,本节使用31 个偶极子天线,按照阵元间距0.5λ组成均匀直线阵列作为模型.在距离阵列中心15λ的轴线位置生成3λ的均匀场,将改进的时间反演和传统时间反演的均匀场生成结果进行对比.在这里将各阵元的辐射能量按照辐射能量最大值归一化处理,即阵元最大辐射能量为1.两种方法下各个阵元辐射能量的幅度和初始相位如图8 所示.

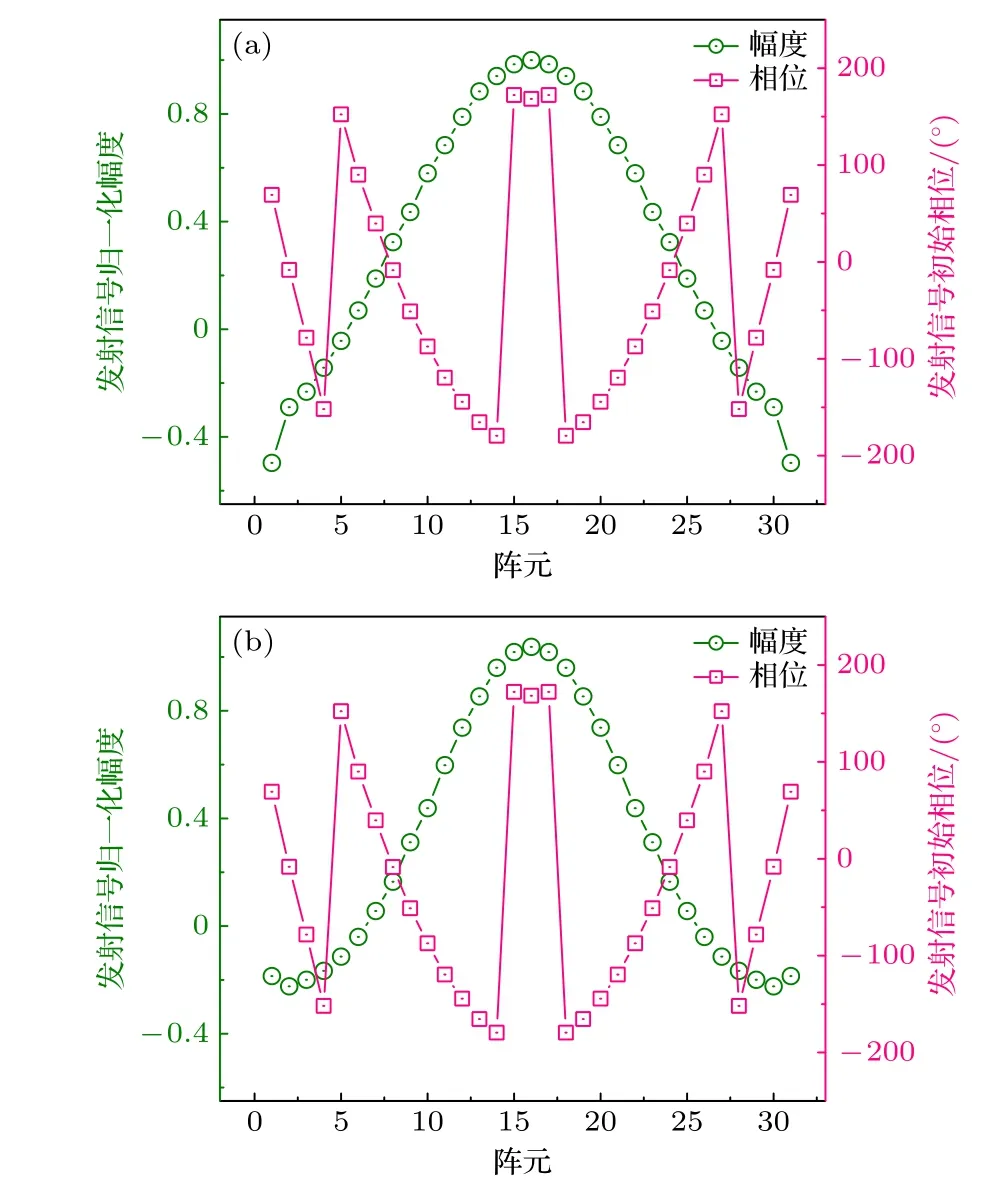
图8 各阵元辐射能量的幅度和初始相位 (a)本文提出的改进时间反演方法;(b)传统的时间反演方法Fig.8.Amplitude and initial phase of radiation energy of each array element: (a) Improved time reversal method proposed in this paper;(b) traditional time reversal method.

两方法在目标位置的合成场结果如图9 所示.可以看出改进时间反演方法(角频率大小÷反演信号幅度)的合成场在目标区域具有更佳的平坦度,第一零点的间距更小,能量更加集中在目标区域.而使用传统时间反演方法(角频率大小×反演信号幅度),在中心处出现最大能量后几乎无平坦区域,直接向两侧开始衰减.这是因为改进的时间反演方法中,通过角频率除以反演信号幅度,预先弥补了由于路径损耗造成的幅度衰减,从而使合成场场型更好.

图9 两种时间反演方法在目标位置的合成场对比Fig.9.Comparison of two time reversal methods in synthetic field of target location.

与一维均匀场的分析相同,对于生成二维均匀场,由于不同阵元到达目标均匀场中心距离不同而所需的幅度和相位优化,同样可以通过时间反演方法获取,在这里不再赘述.

4 实验验证

为了进一步验证本文提出的基于角谱域和时间反演合成任意均匀场方法的可行性,展现该方法在均匀场位置、大小以及偏转角度等方面控制的灵活性,本节采用CST STUDIO SUITE 2021 进行全波仿真实验验证.

4.1 基于等空域直线阵列的一维均匀微波场赋形

图10 展示了合成一维均匀微波场所需的直线阵列,阵列由31 个工作在6 GHz 的偶极子等间距组成,偶极子沿纸面垂直放置,其中偶极子的物理尺寸为:L1=1.5 mm,L2=1 mm,L3=20.5 mm以及阵元间距d=0.5λ(λ=50 mm).

图10 用于合成目标均匀微波场的等空域直线阵列Fig.10.Isospatial linear array for synthesizing uniform microwave field of target.

表1 中列举了5 种不同形式的一维均匀场,并描述了其空域、角谱域表达式以及各个阵元相对于均匀场中心的夹角θn.通过(2)式和(4)式可以算出合成该均匀场各角频率分量对应的大小,并利用时间反演方法获取各个阵元对应的幅度优化值an和相位优化值φn,最后将得到的幅度和相位赋予对应的阵元,激励后得到的场分布如图11 所示.

表1 5 个目标场对应的空域、角谱域表达式以及各阵元的投影夹角Table 1. Five target field expression spatial domain,spatial frequency domain and projection angle of each element.

图11(a)左、(b)左、(c)左、(d)左和(e)左分别展示了基于角谱域和时间反演相结合的方法,利用直线阵列在xOz面合成的电场分布图,图11(a)右、(b)右、(c)右、(d)右和(e)右则分别展示了相应坐标函数线上的场分布.可以看出,目标场1、目标场2 和目标场3通过本文提出的方法,在目标位置合成的电场其幅度都在-3 dB以上,并且在0.5λ的范围内快速滚降至零点,因此可以视为具有明显分界线的均匀场.

对于目标场4,虽然在目标区域附近有大于-3 d B的电场,但是合成场场型发生变化与理论分析求得的合成场并没有良好的匹配.这是因为在理论分析中以均匀场中心位置为基准,假设每个阵元只对目标场贡献唯一角频率.但是实际上,由于目标场处于阵列的笛卡儿坐标系近场区域,各个阵元从目标场一侧到另一侧对应的角频率以及到达时的初始相位并不相同,所以按中心位置计算角频率为近似等效,且近似程度随着目标场大小的增大而减小.前3 个目标场合理均衡均匀场的大小和位置,使得仿真结果与理论近似结果基本保持一致;第4 个目标场斜率过大,各个阵元对目标区域贡献的角频率无法近似等效为中心点对应的角频率,到达目标区域的初始相位也不相同,最终导致仿真结果与理论近似结果出现偏差.目标场5 相对于目标场4 的中心位置向左平移4.5λ,从图11(e)右可以看出,场型得到明显改善,在(-7.5λ,10λ)处生成了与x轴不平行的均匀场.因此在考虑微波传播中的衰减和时延的情况下本方法依然有效.

4.2 基于均匀栅格平面阵列的二维均匀场赋形

图12 展示了合成二维均匀场的平面阵,阵列由21×21 个工作在6 GHz 的贴片天线按照0.5λ(λ=50 mm)等间距构成,其中贴片天线表面金属贴片对应的物理尺寸为,L1=22.5 mm,L2=15 mm.

图12 用于合成目标均匀微波场的均匀栅格平面阵Fig.12.Uniform raster planar array for synthesizing uniform microwave field of target.

表2 和表3 列举了3 种不同形式的二维均匀场并描述了其空域、角谱域表达式以及各个阵元相对于目标均匀场中心的夹角θn和φn.将对应投影夹角以及角谱域表达式代入(8)式和(9)式,可以求出通过图12 阵列合成该目标均匀场所需要的各个角频率分量大小.

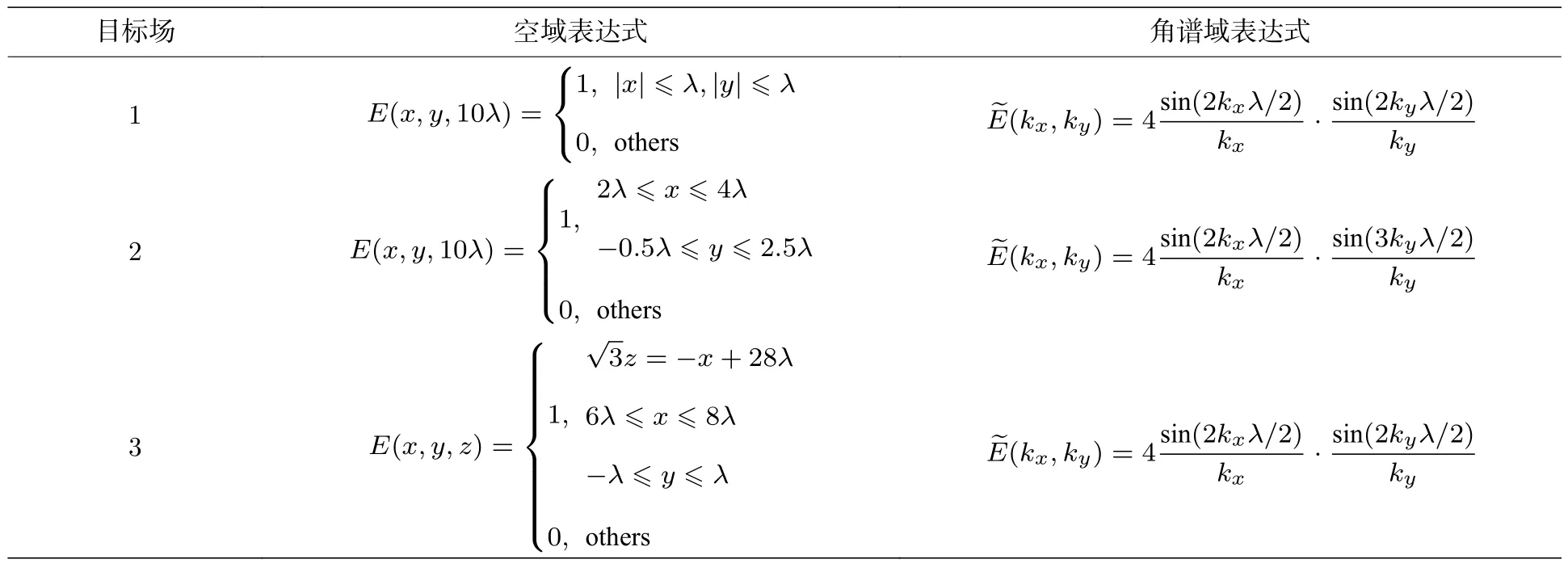
表2 3 个目标场对应的空域、角谱域表达式Table 2. Three target field expression spatial domain,spatial frequency domain.

表3 3 个目标场对应的各阵元的投影夹角Table 3. Three target field projection angle of each element.

图13、图14 和图15 分别展示了通过图12 所示阵列生成表2 中3 个目标场的电场图.对于目标场1 即均匀场处于阵列的正上方10λ处,其对应的角谱域主瓣信息完整且对称,从图13(a)可以看出在目标区域生成了指定大小的均匀场,在均匀场边界±λ的位置有-20 dB的零点,与周围空间具有较好的隔离效果.并且从图14(b)可以看出,利用时间反演优化各个阵元的幅度和相位后,能量从阵面的位置开始逐渐向中间叠加汇聚,最终在指定位置10λ处形成聚焦斑,并在后续的传播中分散.因此有别于通过阵列在角远场区域生成平顶波束进而产生均匀场,利用时间反演方法可以在近场区域指定位置产生均匀场.此外,为了进一步凸显本文提出方法的灵活调节能力,表2 还展示了改变均匀场形状和位置的目标场2 以及旋转均匀场,使其不再与阵面平行的目标场3.需要指出的是,利用时间反演方法,由于在目标区域不存在吸收源,电磁波在指定位置汇聚后会继续扩散传播[21],使得实际生成的均匀场略大于目标场.但是在指定区域的电场强度大于-3 dB,因此并不影响本文方法的灵活调控能力.这些仿真结果结合第2 和第3 节实验分析有力地证明了本文所提出的方法的可行性.

图13 表2 中目标场1 近场电场图 (a) z=10λ 对应的xOy 平面归一化电场图;(b) y=0λ 对应的xOz 平面归一化电场图Fig.13.Near-field electric field diagram of target field 1 in Table 2: (a) xOy plane normalized electric field diagram corresponding to z=10λ;(b) xOz plane normalized electric field diagram corresponding to y=0λ.

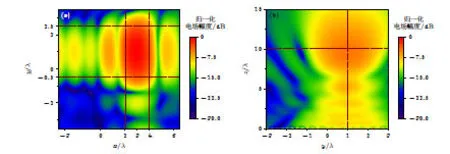
图14 表2 中目标场2 近场电场图 (a) z=10λ 对应的xOy 平面归一化电场图;(b) x=3λ 对应的yOz 平面归一化电场图Fig.14.Near-field electric field diagram of target field 2 in Table 2: (a) xOy plane normalized electric field diagram corresponding to z=10λ;(b) yOz plane normalized electric field diagram corresponding to x=3λ.

图15 表2 中目标场3 近场电场图 (a) z=-x+28λ 平面归一化电场图;(b) y=0λ 对应的xOz 平面归一化电场图Fig.15.Near-field electric field diagram of target field 3 in Table 2: (a) z=-x+28λ plane normalized electric field diagram;(b) xOz plane normalized electric field diagram corresponding to y=0λ.

5 结论

对微波场进行自由灵活地调控能够充分发挥阵列天线的潜能.本文在文献[24]的基础上进行升级,其显著亮点是抛弃了臃肿的半圆形和伞形阵列,利用直线阵列以及均匀栅格平面阵列,在笛卡儿坐标系近场区域,实现了对均匀场包括距离、形状以及偏转角度在内的灵活调控.本文通过对均匀场对应的角谱域主瓣进行分析,证明了均匀场主要信息集中在角谱域的主瓣中,生成均匀场至少需要1/2 的角谱域主瓣信息以及1/2 的角谱域第一副瓣信息.并巧妙地利用了时间反演方法,实现了各个阵元在目标区域的空时同步聚焦.进一步,通过偶极子和贴片天线组阵验证了基于角谱域和时间反演方法合成任意均匀场的可行性.