基于混合导电机制的新型TMOSFET三值逻辑反相器*

马鑫 芦宾† 董林鹏 苗渊浩

1) (山西师范大学物理与信息工程学院,太原 030031)

2) (西安工业大学,陕西省薄膜技术与光学检测重点实验室,西安 710032)

3) (中国科学院微电子研究所,微电子器件与集成技术重点实验室,北京 100029)

三值逻辑技术相比于二值逻辑,不仅能够提高芯片信息密度,还能进一步降低电路功率损耗和系统设计复杂度.然而采用传统的二值逻辑器件搭建三值逻辑电路所需要的元器件数量较多,而且需借助无源元件,这反而牺牲了三值逻辑的优势.借助新型的二维材料也可以实现三值逻辑器件,这种方式需要的元器件数量少,且不需要借助无源元件,但是却面临制备工艺不成熟无法批量生产的问题.目前还没有能够兼容于传统互补金属氧化物半导体工艺的低功耗三值逻辑门电路,针对这一问题,本文将载流子隧穿机制与漂移扩散机制相结合,提出混合机制的隧穿金属氧化物半导体场效应晶体管(TMOSFET),并对其工作原理进行了深入分析,研究了基于TMOSFET 的三值逻辑反相器工作原理,分析了三值逻辑反相器输出3 种状态所对应输入电压范围相当的必要条件,对于后续三值逻辑电路设计具有一定的借鉴意义.

1 引言

在过去几十年中,互补金属氧化物半导体(complementary metal-oxide semiconductor,CMOS)技术随摩尔定律的发展,器件特征尺寸不断缩小,电路集成度不断提高,但随着其尺寸缩小至纳米尺度,器件短沟道效应越来越严重,集成电路静态功耗不断增加,甚至超过动态功耗已成为集成电路功耗的主要来源[1-3].目前以CMOS 为基础的二值逻辑处理器性能很快触顶,为了进一步推动高性能低功耗集成电路的发展,三值逻辑技术被广泛研究.相比于仅采用{0,1}两种状态的二值逻辑,三值逻辑使用{0,1,2}或{－1,0,1} 3 种状态表示信息,其信息表达能力更强[4].对于给定数量的晶体管,三值逻辑可以表达更丰富的信息,当表达相同的信息时,三值逻辑能够减少所需的晶体管数量及互联,这不仅能够使系统设计的复杂度降低约37%,还可以进一步降低电路功率损耗[5-7].目前,三值逻辑的巨大优势已使其成为微电子和计算机领域的研究热点,被认为是超摩尔定律时代持续提升系统性能和信息密度的有效途径之一.

一般情况下,人类对问题的看法并不是只有“真”和“假”两种答案,还有一种“不知道”,这在二值逻辑学中是无法表达的.然而在三值逻辑中,可以用“1”代表“真”,“－1”代表“假”,“0”代表“不知道”,更接近人类大脑的思维方式.实际上人脑被认为是一个三值突触权重的低功耗系统,尽管其包含1000 亿个神经元和100 万亿个突触,功耗却仅有20 W 左右[8,9].三值逻辑更接近人脑的运行原理,基于三值逻辑的神经网络不仅比二值逻辑更为精简,而且在同样的模型结构下,三值神经网络还具有更强的表达能力[10].因此,三值逻辑更符合计算机在神经形态计算中的发展趋势[11],可以为模糊运算和自主学习提供更高效的实现途径.

通常三值逻辑门电路的实现主要有两种方法.第1 种方法采用传统的二值逻辑金属氧化物半导体场效应晶体管(mental-oxide-semiconductor field-effect-transistor,MOSFET)直接搭建三值逻辑门电路[12-15],该方法能够兼容于传统的CMOS工艺,便于批量化生产,但实现一个三值门电路所需要的元器件数量较多,而且通常需要借助无源元件或者双极性电源,这反而增大了芯片面积和系统设计复杂度,无法将三值逻辑本身的优势发挥出来.此外,由于MOSFET 的短沟道效应,这种方法还面临着摩尔定律功耗限制和信息密度无法有效提升的矛盾.第2 种方法直接采用具有3 种状态的三值逻辑器件,这类器件除了具有“开”和“关”两种状态外,还具有一种处于“开”和“关”之间的中间态.这种方法不需要借助无源元件和双极性电源,且每个三值反相器只需要两个三值逻辑器件,因此能够降低芯片面积和系统设计复杂度,可以将三值逻辑的优势发挥出来.然而为了获得具有3 种状态的逻辑器件,通常需要采用与传统CMOS 工艺不兼容的新型二维材料[16-19],如有机材料及相变材料等,这不仅使得中间态的形成很不稳定,而且所设计的逻辑门电路面临新型材料制备工艺不成熟而无法批量化生产的问题.因此,目前还没有能够兼容于传统CMOS 工艺的低功耗三值逻辑门电路,这在很大程度上限制了三值逻辑芯片及其设计方法学的研究.

针对以上问题,本文将载流子隧穿机制和漂移扩散机制相结合,提出混合机制的隧穿金属氧化物半导体场效应晶体管(TMOSFET),该结构可以输出3 种稳定状态,所实现的三值逻辑,不仅不需要借助无源器件,而且结构简单,制备工艺能够兼容于传统CMOS 平台.

2 器件结构与仿真设置

图1 为一个n 型TMOSFET 结构示意图,器件参数如表1 所列,其中Source -Ⅰ,Channel -Ⅰ和Drain 构成nTFET 器件,Source -Ⅱ,Channel -Ⅱ和Drain 构成nMOSFET 器件.可以看出,TMOS FET 相当于一个nTFET 和nMOSFET 的并联,其结构简单,制备工艺能够兼容于传统CMOS 工艺,而且只需在n 型器件结构的基础上,改变源区、沟道和漏区对应掺杂类型便可得到相应的p 型器件.为了便于后续器件原理分析,图1 中的AA0为氧化层与半导体界面正下方3 nm 处的切线.

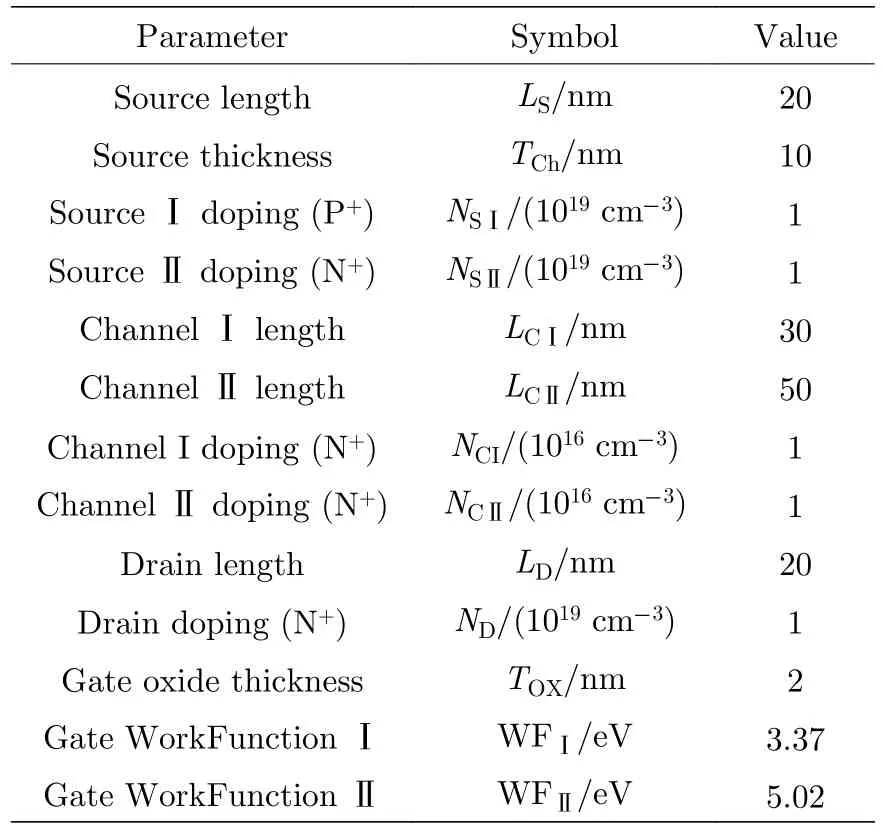
表1 n 型TMOSFET 结构参数Table 1. Structure parameters of n-type TMOSFET.

图1 n 型TMOSFET 器件结构示意图Fig.1.Structure diagram of n-type TMOSFET.

通过TCAD 二维数值仿真工具对所设计的器件及三值逻辑电路进行研究,为了能够考虑非均匀电场对隧穿过程的影响,采用非局域带带隧穿(band-to-band tunneling,BTBT)模型计算载流子隧穿路径和概率[20].此外,仿真过程中还考虑了掺杂相关的迁移率模型,高电场速度饱和模型以及Shockley-Read-Hall 复合等模型[21].

3 TMOSFET 器件原理分析

图2 给出了漏极电压VD=0.5 V 时nTMOS FET 的ID-VG转移特性曲线(其中ID为漏极电流,VG为栅极电压),可以看到nTMOSFET 的特性曲线与传统MOSFET 的特性曲线有明显的不同,在转折电压Vturn=0.6 V 左右存在明显的转折过程,这一转折使得nTMOSFET 表现出了3 种状态,也就是关态、开态以及处于开关状态之间的中间态,nTMOSFET 的三态特性使其十分适合于三值逻辑电路的设计.

图2 nTMOSFET ID-VG 特性曲线Fig.2.ID-VG characteristic curve of nTMOSFET.

实际上这是由Vturn前后不同的导电机制所导致的,为了进一步说明,图3(a)给出了曲线转折前VG=0.3 V 时,沿切线AA0的能带分布图,可以看出当VG=0.3 V,Source -Ⅰ区导带(EC)与Channel -Ⅰ区的价带(EV)发生交叠,因此Source -Ⅰ区的价带电子可以隧穿进入Channel -Ⅰ区,并被Drain 区收集形成电流.此时,Source -Ⅱ区与Channel -Ⅱ区之间的势垒较高,Source -Ⅱ的电子无法越过势垒进入Channel -Ⅱ区,因此器件的电流主要由Source -Ⅰ到Channel -I 的隧穿电流主导.图3(b)给出了VG=0.3 V 时的电子隧穿概率及电流密度分布情况,可以看出此时在Channel -Ⅰ中靠近Source -Ⅰ区附近电子隧穿概率较高,而且电流密度主要分布在Channel -Ⅰ区.

图3 VG=0.3 V 时,(a)沿切线AA0 的能带分布图和(b)电子隧穿概率与电流密度分布图Fig.3.(a) Energy band diagram along cutline AA0 and (b) contour mapping of electron BTBT rate and current density at VG=0.3 V.

当VG增至0.9 V 时,如图4(a)所示,Source -Ⅱ与Channel -Ⅱ之间的势垒高度明显降低,这使得Source -Ⅱ区的电子可以通过热发射的形式跨过势垒进入Channel -Ⅱ区,并以漂移扩散的形式被Drain 区收集形成电流.虽然此时Channel -Ⅰ与Source -Ⅰ区的能带依然交叠,甚至隧穿电流更高,但是相比于Source -Ⅱ到Channel -Ⅱ的漂移扩散电流,其对总电流的贡献十分小,因此此时器件电流主要由Source -Ⅱ到Channel -Ⅱ的热发射电流主导.图4(b)给出了VG=0.9 V 时的电子隧穿概率及电流密度分布情况,可以看到,尽管此时在Channel -Ⅰ区依然存在大量隧穿电流,但是器件电流密度却主要分布于Channel -Ⅱ区.

图4 VG=0.9 V 时,(a)沿AA0 的能带分布图和(b)电子隧穿概率与电流密度分布图Fig.4.(a) Energy band diagram along cutline AA0 and (b) contour mapping of the electron BTBT rate and current density at VG=0.9 V.

综上可见,在TMOSFET 中存在两种导电机制,当VGVturn时,器件电流主要由Source -Ⅱ到Channel -Ⅱ的热发射电流主导,由于热发射电流远大于隧穿电流,在Vturn附近电流突然上升,导致传输曲线出现转折,并最终使TMOSFET 器件表现出3 种状态.

4 基于TMOSFET 的三值逻辑反相器

图5 为电学特性匹配的n 型和p 型TMOS FET 转移曲线,其中p 型器件结构与n 型器件相同,具体结构参数如表2 所列.通过TMOSFET设计三值逻辑反相器的电路结构与二值逻辑反相器相同,如图5 插图所示,其中Vin与Vout分别为反相器输入电压与输出电压;VDD为反相器工作电压;S,G,D 分别表示n 型或p 型器件的源极、栅极、漏极.

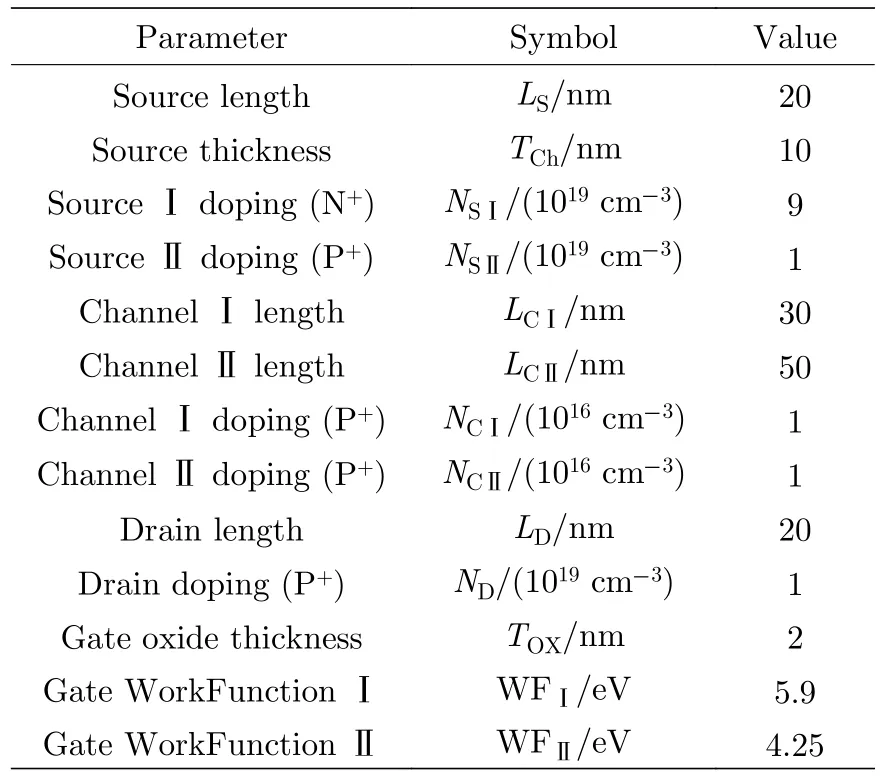
表2 p 型TMOSFET 器件参数Table 2. Structure parameters of p-type TMOSFET.

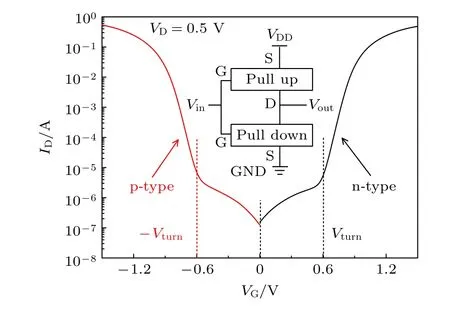
图5 n 型和p 型TMOSFET 器件ID-VG 特性曲线Fig.5.ID-VG characteristic curves of the n-type and p-type devices.

图6(a)给出了电源电压VDD=0.9 V 时的反相器电压传输曲线(VTC),可以看到,反相器输出有明显的3 种状态,即高电平H(“2”),中间电平M(“1”)及低电平L(“0”),其中高电平H 和低电平L 所对应的电压曲线十分平坦,而中间电平M 所对应的电压曲线并不平坦,而是随输入电压升高缓慢下降.对于理想的三值逻辑反相器,这3 种状态应是等概率的,也就是电平H,M 和L 所对应的输入电压范围应当相等.图中VIL,VIML,VIMH和VIH分别为斜率为-1的点对应的输入电压值,RH,RM和RL分别为高电平H、中间电平M 和低电平L所对应的输入电压范围,可以看到虽然RM略微小于RH和RL,但是3 种状态所对应的输入电压范围基本相当.反相器瞬态特性如图6(b)所示,输入信号频率为25 kHz,从L 上升到M 和从M 上升到H 的上升时间τr=0.07 μs,从H 下降到M 和从M 下降到L 的下降时间τf=0.09 μs,可以看到,所设计电路能够实现三值逻辑反相功能.

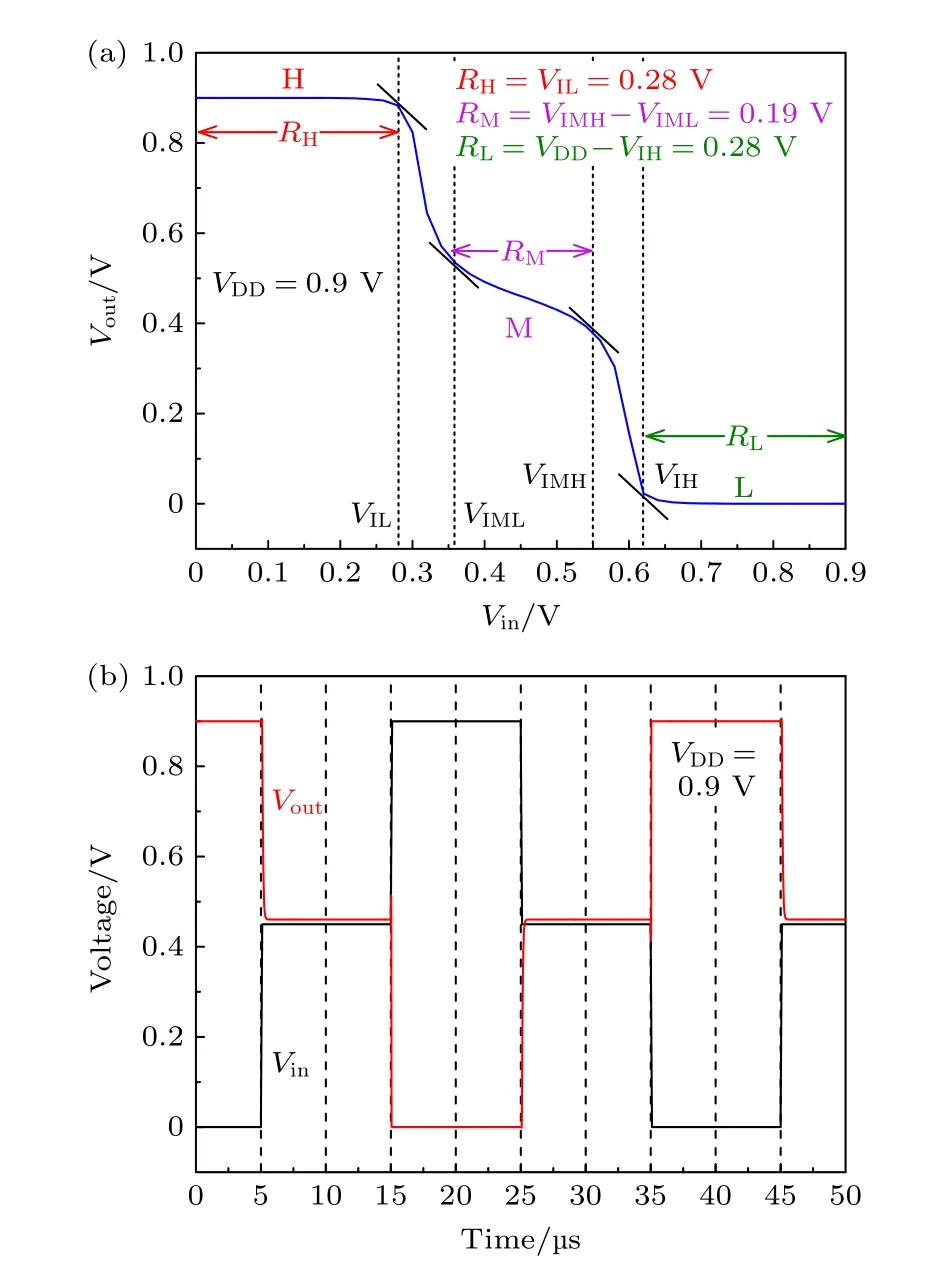
图6 反相器的(a) VTC 曲线和(b)瞬态特性曲线Fig.6.(a) VTC curve and (b) transient response of the proposal ternary inverter.

图7 给出了不同VDD下的反相器VTC 曲线,对比可发现,随着VDD从0.9 V (1.5Vturn)逐渐减小,中间电平M 所对应的电压曲线逐渐变得平缓,因此其所对应输入电压范围RM逐渐变大,而高电平H 和低电平L 所对应输入电压范围RH与RL逐渐减小.直到VDD减小到VDD=Vturn=0.6 V时,高电平H 和低电平L 已近乎消失,VTC 曲线主要由中间电平M 和过渡区组成,因此三值反相器正常工作时工作电压VDD应大于Vturn.随着VDD从0.9 V 增大,VTC 曲线表现出相反的规律,中间电平M 所对应电压曲线变得越来越陡峭,其所对应输入电压范围RM逐渐减小,而高电平H 和低电平L 所对应电压范围则逐渐增大.直到VDD增大到VDD=1.1 V 时,中间态M 已变得很不明显,当VDD≥2Vturn=1.2 V 时,中间电平M 已彻底消失,此时VTC 曲线已完全变成了二值逻辑反相器曲线.

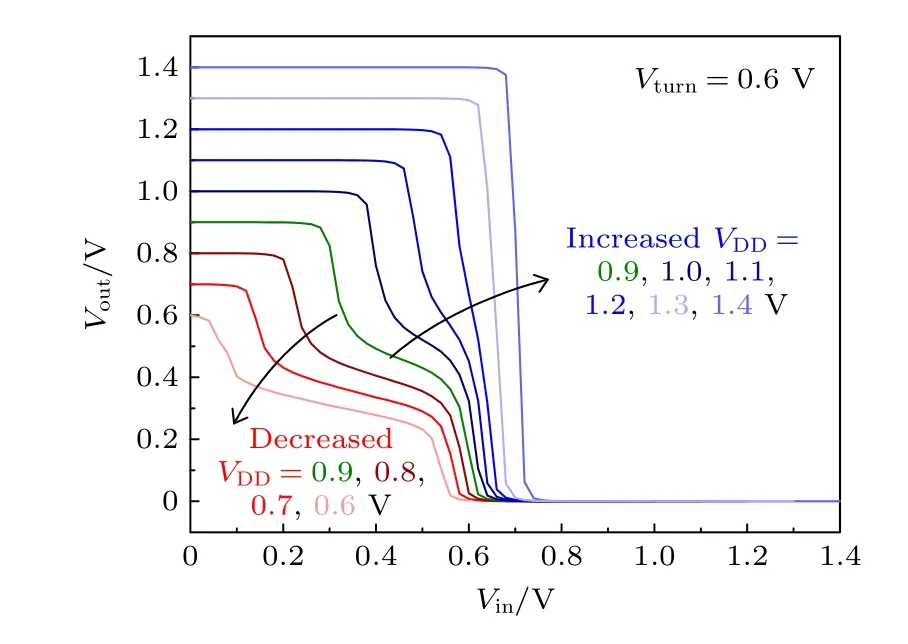
图7 不同VDD 下三值逻辑反相器的VTC 曲线Fig.7.VTC curves of ternary inverter at various VDD.

可见,电源电压VDD对反相器工作特性影响较大,在忽略过渡区的情况下,最优的VDD≈1.5Vturn,此时反相器表现出明显的3 种状态,且每种状态所对应的输入电压范围基本相当.VDD减小,将导致中间电平M 所对应电压范围变宽,而高低电平所对应电压范围变窄,直至VDD=Vturn时,高低电平几乎消失;VDD变大,将导致高低电平所对应电压范围变宽,而中间电平M 所对应电压范围变窄,当VDD>2Vturn时,中间电平完全消失,三值反相器退化为二值逻辑反向器.

在三值逻辑反相器中,nTMOSFET 的栅极输入电压VGSn=Vin,而pTMOSFET 的栅极输入电压VGSp=Vin－VDD,因此只需要将pTMOSFT的传输曲线向右移动VDD,即可得到反相器IDVin曲线.图8(a)给出了VDD=Vturn=0.6 V 时的ID-Vin曲线,可以看到,输入电压Vin从0 V 逐渐增大到VDD/2 的过程中,p 型器件电流大于n 型器件电流,即p 型器件的导通电阻RONp小于n 型器件导通电阻RONn,因此在这一过程中输出电压Vout>VDD/2,如图7 所示.当Vin=VDD/2 时,n 型器件的电流与p 型器件电流大小相等,两者导通电阻也相等,此时Vout=VDD/2.当Vin继续增大,n 型器件电流大于p 型器件电流,RONn小于RONp,因此Vout

图8 反相器ID-Vin 曲线 (a) VDD=Vturn;(b) VDD=0.9 V;(c) VDD=2Vturn=1.2 V;(d) VDD=1.4 VFig.8.ID-Vin curves of ternary inverters: (a) VDD=Vturn;(b) VDD=0.9 V;(c) VDD=2Vturn=1.2 V;(d) VDD=1.4 V.

为了出现明显的高低电平,实现三值逻辑,应使n 型和p 型器件电流相差较大,即RONp和RONn存在较大差异,才能使得Vout接近0 V(低电平L)或者VDD(高电平H),这就要求p 型器件传输曲线继续向右移动,也就是需要VDD>Vturn.

图8(b)给出了VDD=0.9 V 时的曲线,可以看到,当0 V

然而如果继续增大VDD,n 型和p 型器件电流均受隧穿电流主导的区域,也就中间电平M 所对应的电压范围将会逐渐变窄,直到VDD=2Vturn时,中间电平M 已经消失,如图8(c)所示.此时Vin从0 V 上升到VDD的过程中,只有两种明显状态,即 当0.0 V2Vturn的情况与VDD=2Vturn情况类似.

以上分析可以发现,当VDD2Vturn时,反相器只能输出高电平H 和低电平L,只有当Vturn

图9 RH/VDD 和RM/VDD 随VDD 的变化曲 线Fig.9.Variation of RH/VD and RM/VDD with VDD.

Vturn是器件电压传输曲线的关键参数,其大小可以通过WFII进行调整,图10 给出了不同Vturn下的器件特性曲线,相应的WFII参数如表3所列.由于WFII主要控制器件Channel -Ⅱ区的势垒高低,而不对Channel -Ⅰ区的电势产生影响,因此随着WFII变化,器件的漂移扩散电流曲线水平移动,而隧穿电流部分并不发生变化,最终使得器件从隧穿电流到漂移扩散电流的转折电压Vturn发生变化.

表3 不同Vturn 所对应的WFⅡTable 3. WFⅡ corresponding to different Vturn..

图10 不同Vturn 时TMOSFET 转移特性曲线Fig.10.ID-VG characteristic curves of TMOSFETs with different Vturn.

图11(a)给出了不同Vturn下三值逻辑反相器的VTC 曲线,可以看出,随Vturn的增大,RM逐渐增大,RH和RL逐渐减小.图11(b)给出了RH/VDD和RM/VDD随Vturn的变化曲线,当Vturn满足Vturn=VDD/1.4 ≈ 0.63 V 时,3 种状态所占比例相等约为0.27,这与图9 中得出的结论是一致的.

图11 不同Vturn 时的(a)三值反相器的VTC 曲线和(b) RH/VDD 及RM/VDD 随VDD 的变化规律Fig.11.(a) VTC curves of ternary inverter and (b) variation of RH/VD and RM/VDD with VDD at different Vturn.

在CMOS 反相器中,互补的nMOS 和pMOS器件只有一个导通,这使得电路的静态功耗很低,而我们所提出的TMOSFET 三值反相器只有在H 和L 电平时才是互补的.当反相器输出M 电平时,nTMOSFET 和pTMOSFET 同时工作在半导通状态,器件的中间态电流对反相器特性有较大影响.器件的中间态电流主要由Channel -Ⅰ区的隧穿电流主导,因此改变WFⅠ可以改变Channel -Ⅰ区的能带高低,从而控制中间态电流的大小,同时并不影响Channel -Ⅱ区的能带分布和开态电流的大小,如图12(a)所示.可以看到,随着WFⅠ减小,中间态电流增大,且中间态电流曲线逐渐平缓,但是器件导通电流并没有发生变化.图12(b)给出了相应的三值反相器VTC 曲线,随着器件中间态电流曲线变得平缓,VTC 曲线M 所对应电压曲线也逐渐平缓,所对应输入电压范围RM变大,这就意味反相器中间电平M 与高电平H、低电平L 的区分度更大,具有更强的抗干扰能力.

图12 不同WFⅠ下,(a)器件的ID-VG 特性曲线和(b)三值反相器VTC 曲线Fig.12.(a) ID-VG characteristic curves and (b) VTC curves of ternary inverter at different WFⅠ.

图13(a)给出了WFⅠ对反相器瞬时特性的影响,随着WFⅠ增大,器件中间态电流减小,使得电容充放电时间变长,反相器输出从电平H 跳变到电平M 的延迟时间从0.06 μs 增大到0.18 μs,从电平L 跳变到电平M 的时间从0.04 μs 增大到0.15 μs,致使反相器速度变慢.中间态电流的变化还会影响到电路功耗,图13(b)给出了反相器输出在不同电平之间跳变时,从电源到地的电流变化,可以看到,当反相器输出H 和L 电平时,电源电流相对较小,而当反相器输出M 电平时,电源到地的电流较大,这是因为反相器处于H 和L 电平时,n 型器件和p 型器件只有一个器件导通,不存在从电源到地的直流通路,而当其处于M 电平时,n 型和p 型器件均处于中间半导通状态,因此反相器静态功耗主要由M 电平主导.随着WFⅠ变小,器件中间态电流和关态电流同时变大,导致反相器电流也逐渐增大,而且器件关态电流随WFⅠ减小而增大的速度比中间态电流增大的速度要快,当WFⅠ=3.07 eV时,关态电流已接近中间态电流,此时反相器输出3 种状态时的电流大小相当,共同决定了反相器的静态功耗,如图13(b)中的黑线所示.反相器在一个周期内的总功耗PT可以描述为

图13 不同WFI 时三值反相器的(a)瞬态特性和(b)电流曲线Fig.13.(a) Transient response and (b) current curves of ternary inverter at different WFI.

式中T为周期,IVDD表示反相器从电源到地的电流大小,t表示时间为积分变量,其中VDD是常数,第2 项积分项相当于反相器电流与时间轴所围成的面积.通过差分求和,可以计算出WFⅠ分别为3.57,3.37,3.07 eV 时,一个周期内反相器功耗分别为15.1,32.1,98 pJ,可见,反相器功耗随WFⅠ的减小和器件中间态电流的增大而增加.

可见,TMOSFET 中间态电流对反相器的稳定性、速度和功耗有很大影响,随中间态电流增大,VTC 曲线中间电平M 所对应电压曲线变得平坦,反相器稳定性和抗干扰能力增强,速度也变快,但这是以牺牲功耗为代价的,实际反相器在设计时需要根据电路的应用场景在稳定性、速度和功耗之间进行折中考量.

最后,还需要强调的是,半导体器件在实际制备过程中一般会经历多次高温工艺,掺杂原子横向扩散,难以形成突变隧穿结,再加上缺陷辅助隧穿等因素的影响,使得TFET 器件突破60 mV/dec亚阈值摆幅(SS)十分困难,对器件制备工艺要求很高.但本文所提出的TMOSFET 结构中,TFET主要工作在电流变化较为平缓的区间,也就是SS较大的区域,因此并不要求其有很小的SS,这很大程度上降低了对器件性能的要求和制备工艺的难度.再者,TMOSFET 器件结构简单,制备工艺能够兼容于CMOS 工艺,因此,本文提出的TMOS FET 无论从器件性能还是制备工艺方面都比传统的TFET 更容易实现.

5 结论

本文将载流子隧穿机制和漂移扩散机制结合提出混合机制的TMOSFET,并对其工作原理进行了深入分析,TMOSFET 的传输曲线具有关态、开态以及处于开关状态之间的中间态,共3 种状态,这一特性使其十分适合于三值逻辑设计.此外,本文还研究了基于TMOSFET 的三值逻辑反相器的工作原理,分析了反相器三态输出的条件,发现当工作电压VDD与器件转折电压Vturn满足VDD/Vturn≈ 1.4 时,三值逻辑反相器输出的3 种状态所对应输入电压范围相当.此外,还分析了器件特性对反相器稳定性、速度以及功耗的影响,研究成果对于后续三值逻辑电路设计具有一定的参考价值.