“模型思想”在2022年新高考全国Ⅱ卷中的应用探析
福建师范大学附属福清德旺中学 (350319) 周 丹
福建省福清市进修学校 (350300) 林新建
数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法建构模型解决问题的素养.数学模型是借用数学的语言讲述现实世界中的数量、图形有关的故事,使数学走出了自我封闭的世界,构建了与现实世界的桥梁.在解题过程中,“模型思想”的建立,能帮助我们更好地挖掘模型或者建构模型,从而将复杂的问题化归转化为简单的数学模型进行求解,进一步培养学生的核心素养,在教学中具有实际的意义.以下就“模型思想”在2022年新高考全国Ⅱ卷中的应用作一探析,以飨读者.
一、挖掘模型
应用“模型思想”在题中挖掘所蕴藏的数学模型,借助找出的数学模型简化运算,将问题轻松解决.
A.-6 B.-5 C.5 D.6


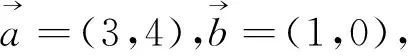
评析:本题中强调用数学的眼光去直观想象并进行数学抽象,一步步地抽象出菱形模型,是“模型思想”的应用,整个过程进行逻辑推理,培养了学生的数学眼光、数学思维和数学核心素养.
例2 (第12题)若x,y满足x2+y2-xy=1,则( ).
A.x+y≤1 B.x+y≥-2
C.x2+y2≤2 D.x2+y2≥1
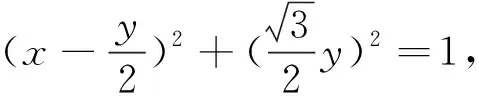



分析:由|MA|=|NB|可知,线段MN中点与线段AB中点重合,这样就可以将问题抽象为中点重合模型进行求解.


评析:本题通过数学抽象,抽象出中点重合的模型,注重对数学运算的考查,中点模型的给出可以简化运算,而圆锥曲线简化运算实际上是基于数学抽象和逻辑推理下的运算简化,进一步也培养了学生的数学抽象和逻辑推理素养.
二、建构模型
应用“模型思想”,借助一些现有模型特征构建满足题意的新模型,或通过观察、分析数学式子特征,建构适当的模型,帮助问题更好、更快地解决.

A.-3 B.-2 C.0 D.1


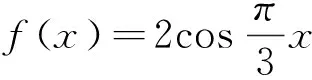
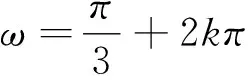
评析:本解法先通过对模型的初步识别,发现这个模型与两角和余弦公式的模型类似,由此受到启发,通过待定系数法建构合理的建模,实现从特殊到一般,再从一般到特殊的转化,实际上也是数学抽象的培育过程.
例5 (第22题)已知函数f(x)=xeax-ex.
(1)当a=1时,讨论f(x)的单调性;
(2)当x>0时,f(x)<-1,求a的取值范围;
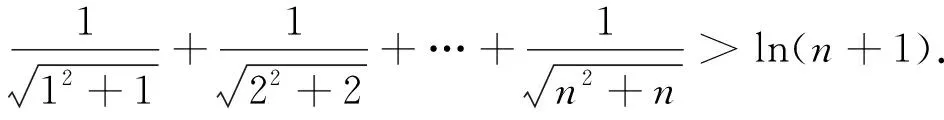

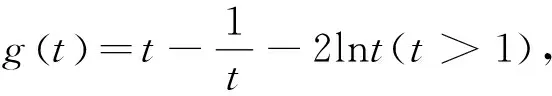
评析:引导学生分析观察数学式子,猜测探究适当的数学结论,给出解释或证明,培养学生直观想象,数学抽象,逻辑推理,数学建模核心素养.
三、结语
“模型思想”的培养,不止可以帮助学生快速地挖掘或建构合理的模型来解决问题,从而有效地简化求解途径,还能通过数学建模的过程,提高学生发现和提出问题的能力、分析和解决问题的能力.在“模型思想”的培养过程中,教师要引导学生用数学的眼光去观察,用数学的思维去思考,用数学的语言去概括,进一步使学生掌握必备的基础知识和关键能力,培养学生的数学抽象、逻辑推理、数学建模、直观想象、数学运算等素养.

