一道抛物线联考题的变式与推广

湖南省长沙市南雅中学 (410027) 龙 伟

1 试题再现

题目(2023届江西省“新八校”高三上学期第一次联考理数第8题)如图1,抛物线E:y2=2px(p>0)的焦点为F,过F且斜率为1的直线交E于A,B两点,线段AB的中点为M,其垂直平分线交x轴于点C,MN⊥y轴于N,若四边形OCMN的面积等于8,则E的方程为( ).

图1

A.y2=2xB.y2=4x

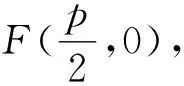
点评：本题考查直线与抛物线的位置关系,由于M为线段AB的中点,所以运用“点差法”表示点的坐标,令直线MC的方程中y=0表示点C的坐标,然后应用三角形面积公式列方程求得p的值得解.

2 试题变式

若上述试题中所得抛物线的方程为已知条件,直线MC与直线AB垂直的位置关系不变,并将直线MC移至过点F,则有下面的若干变式并推广一般性的结论.

变式1 已知抛物线E:y2=4x的焦点为F,过F作两条互相垂直的直线l1,l2,直线l1,l2与分别交于A、B和D,H则|AB|+|DH|的最小值为( ).

(1) 盾构隧道常见病害之间是相互联系的，往往表现为多种病害同时存在，且随着地铁运营时间的增加病害亦会随之加剧。其中，隧道不均匀沉降是导致产生其他常见病害的重要原因之一，也是判断隧道是否稳定的重要依据之一。

A.10 B.12 C.14 D.16

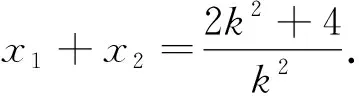
解法2：如图2,E的准线与x轴交于G,过点A作准线的垂线于K1,AK2⊥x轴于k2.

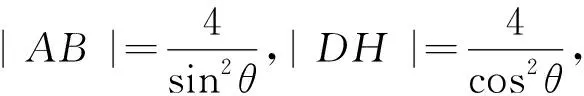
A.64 B.32 C.16 D.10

变式4 已知抛物线E:y2=4x的焦点为F,过F作两条互相垂直的直线l1,l2,直线l1,l2与E分别交于A、B和D、H,则四边形ADBH面积的最小值为( ).

A.64 B.32 C.16 D.10

变式5 已知抛物线E:y2=4x的焦点为F,过F作两条互相垂直的直线l1,l2,直线l1,l2与E分别交于A、B和D、H,若AB的中点为M,线段DH的中点为P,则△FMP面积的最小值为( ).

A.4 B.8 C.16 D.22

变式6 已知抛物E:y2=4x线的焦点为F,过F作两条互相垂直的直线l1,l2,直线l1,l2与E分别交于A、B和D、H,若AB的中点为M,线段DH的中点为P,则直线MP恒过点( ).

A.(2,0) B.(3,0) C.(4,0) D.(8,0)

②若k=1或k=-1,则直线MP的方程为x=3,也过点(3,0).

综上可知直线MP恒过点(3,0).故选B.

3 结论推广

将上述各变式推广到一般形式的抛物线,可有下面相应的结论.

结论1 已知抛物线E:y2=2px(p>0)的焦点为F,过F作两条互相垂直的直线l1,l2,直线l2,l2与E分别交于A、B和D、H,则|AB|+|DH|的最小值为8p.

结论1的证明仿照变式1的证明过程.

结论2的证明仿照变式1、2的证明过程.

结论3 已知抛物E:y2=2px(p>0)线的焦点为F,过F作两条互相垂直的直线l2,l2,直线l2,l2与E分别交于A、B和D、H,则|AB|·|DH|的最小值为16p2.

结论3的证明仿照变式1、3的证明过程.

结论4 已知抛物线E:y2=2px(p>0)的焦点为F,过F作两条互相垂直的直线l2,l2,直线l2,l2与E分别交于A、B和D、H,则四边形ADBH的最小值为8p2.

结论4的证明仿照变式3的证明过程.

结论5 已知抛物线E:y2=2px(p>0)的焦点为F,过作两条互相垂直的直线l2,l2直线l2,l2与E分别交于A、B和D、H,若AB的中点为M,线段DH的中点为P,则△FMP面积的最小值为p2.

结论5的证明仿照变式5的证明过程.

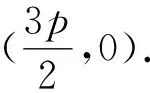
无论是同步教学还是在高考复习中,要常态化地指导学生通过对一些典型问题的探讨和拓展,及时归纳、总结出一些常用的“二级结论”,这对于学生解题能力的提高和数学素养的提升是颇有裨益的.