基于双弹光级联差频调制的应力双折射二维分布测量
李克武, 邱元芳, 崔志英, 毛磊, 王志斌, 匡翠方1,*
(1.浙江大学 光电科学与工程学院,浙江 杭州 310014;2.宁波永新光学股份有限公司,浙江 宁波 315040;3.中北大学 山西省光电信息与仪器工程技术研究中心,山西 太原 030051)
1 引 言
国际标准(ISO10110-2:1996(E))给出了几种典型应用中光学材料和元件的应力双折射的容忍限值,例如偏振、干涉仪器中要求<2 nm/cm,精密光学、天文光学要求不超过5 nm/cm,成像光学、显微光学中要求不超过10 nm/cm等[1]。对光学材料和光学元件的应力进行测试分析,特别是应力分布测试评估,将光学元件应力控制在允许值范围内,是光电系统研制和生产的必要环节。
玻璃、光学晶体等光学材料生长过程、加工过程、装载夹持过程均会引入应力双折射[2-3]。应力双折射不仅会影响光学元件的机械稳定性,而且会带来成像畸变和像散等危害[4]。目前,国内外开展了大量应力双折射测量研究工作,相继提出了偏光干涉、偏振补偿、偏振成像、偏振调制等应力双折射测量方法。偏光干涉法,检测光源依次通过起偏器、样品和检偏器发生干涉,通过成像探测器观测干涉色序,然后计算出应力双折射延迟量[5]。偏振补偿法基于Senarmont补偿原理,在偏光干涉的基础上在样品和检偏器之间加入一个1/4波片或相位延迟器,通过旋转波片或检偏器观测偏振角来实现应力双折射测量[6]。偏光干涉和偏振补偿测量方法具有仪器结构简单,测量孔径大等优势,特别是,基于偏光干涉法建立的数字光弹性应力仪是目前市场主流应力双折射测量产品。但受限于干涉色序计数的判断精度,应力双折射测量分辨率始终无法突破1 nm量级。近年来随着微电子加工工艺的发展,像元级偏振器被研制应用于CMOS成像探测器上,开发出偏振成像探测器,并应用于应力双折射延迟量成像研究,单次成像便能实现应力双折射分布测量[7]。但目前开发的偏振CMOS成像探测器无法实现圆偏振分量探测,并且每个像元上偏振器一致性差异,进而限制了应力双折射延迟量测量的动态范围和精度。
基于法拉第旋光器、液晶可变延迟器、电光调制器和弹光调制器等偏振调制技术,开发了偏振调制型应力双折射测量方法[8-9],通过调制信号的分析提高了信噪比,实现了较高精度的的应力双折射测量,但偏振调制方法测量过程复杂,测量系统成本昂贵,最为关键的是偏振调制方法多为单点测量,应力双折射分布测量需要扫描样品实现。本文基于弹光调制技术具有高调制频率、大通光孔径、高调制纯度、工作稳定等应用优势[10-11],开展双弹光级联差频调制,结合数字锁相数据处理技术实现高速、高精度的应力双折射测量,系统搭载二维电动平移台来扫描样品,实现高空间分辨,大空间范围的应力双折射分布测量研究。
2 应力双折射测量原理
光学材料、光学元件中存在应力时,最显著的光学效应是会产生双折射现象。入射光沿两个应力主轴方向分解为振动方向相互垂直、传播速度不同的寻常光和非寻常光。两个偏振光通过具有应力分布的光学材料或元件出射后会产生一个光程差。该光程差也称之为应力延迟量。同时,单位厚度上的延迟量定义为应力双折射。应力延迟量和应力双折射都能够直接用来评估光学材料或元件的应力情况,描述为[9,12]:
其中:C为材料应力光学系数,d为材料厚度,σ1和σ2为两个方向相互垂直的主应力。由式(1)可知,通过对应力延迟量的测量能够进一步确定应力双折射大小,应力等大小,因此应力延迟量是光学材料、光学元件中应力测量评估的基本物理量。
利用弹光调制技术的高调制频率、大通光孔径、高调制纯度、宽光谱范围等应用优势,本文基于弹光调制技术,结合数字锁相数据处理技术,建立应用双弹光级联差频调制的应力测量方法。基于双弹光级联差频调制实现应力延迟量和快轴方位角同时测量,并通过二维电动平移台扫描样品来实现样品应力延迟量的二维分布测量,测量方案基本原理如图1所示。
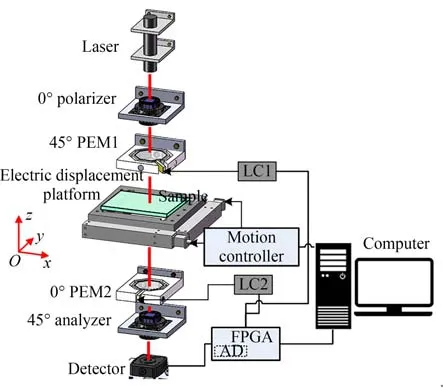
图1 应力双折射二维分布测量方案原理图Fig.1 Block diagram of two-dimensional distribution measurement of stress birefringence
如图1所示,以弹光调制器1(PEM1)和弹光调制器2(PEM2)为核心构建偏振分析装置,检测激光依次经过起偏器,两个弹光调制器,再经过检偏器被探测器探测。起偏器和检偏器的透光轴方向分别设置为0°和45°,两个弹光调制器的调制快轴方向分别设置为45°和0°,使整个偏振分析装置中偏振器透光轴方向、弹光调制快轴方向依次相差45°。为了能够实现应力延迟量和快轴方位角同时测量,本文方案中选用的两个弹光调制器谐振工作频率不一致,级联工作,构成差频调制偏振分析测量系统。待测样品设置在分析系统的中部。整个检测光信号采用Stokes矢量描述,偏振器、弹光调制器和样品的偏振传输特性采用Mueller矩阵描述较为方便。整个测量方案采用Stokes矢量和Mueller矩阵描述为[13]:
其中:Sout表示出射光的Stokes矢量,Sin表示经0°起偏器后的入射光Stokes矢量,通常表示为Sin=I0[1100]T,其中I0为入射光经起偏器透射的总光强。MPEM1和MPEM2分别表示PEM1和PEM2的Mueller矩阵,且PEM1调制快轴方位角设置在45°,PEM2的设置在0°,所以两个PEM的Mueller矩阵可以描述为[14]:
其中:PEM1和PEM2的相位调制分别用δ1和δ2表示,且可以进一步表示为δ1=δ10sinω1t和δ2=δ20sinω2t,δ10和δ20分别表示两个PEM的相位调制幅值,ω1和ω2分别表示两个PEM的谐振工作频率。为了同时实现应力延迟量和快轴方位角测量,本文方案的关键在于两个PEM谐振工作频率不相等(ω1≠ω2),构成双弹光级联差频调制的偏振分析测量系统。
样品应力延迟量R对应的相位延迟可表述为X=2πR/λ,因此,样品应力双折射的偏振传输特性可以用Mueller矩阵描述为[5-6]:
其中,ρ表示为应力双折射的快轴方位角。
检偏器的透光轴设置在45°方向,其Mueller矩阵表示为:
将式(3)~式(5)表述的PEM、样品和检偏器的Mueller矩阵,连同入射光的Stokes矢量带入式(2),并考虑探测器能够探测到的光强为Stokes矢量的第一个分量,求解获得探测器探测到双弹光级联差频调制的偏振分析测量系统的输出检测光强为:
其中:两个PEM调制项sinδi=sin(δi0sinωit)和cosδi=cos(δi0sinωit)采用第一类贝塞尔函数展开得和1,2,…,k,且为正整数,J0,J2k-1和J2k分别代表第0阶,第2k-1阶,第2k阶贝塞尔级数,PEM1和PEM2分别对应i=1和2。取低阶贝塞尔级数,式(6)进一步改写为:
由式(7)分析可知,样品应力双折射的相关项sin(4ρ)sin2(X/2)被加载在2ω1,2ω2,2ω1+2ω2和2ω2-2ω1等频率信号中,相关项cosX被加载在ω1+ω2和ω2-ω1等频率信号中,相关项cos(2ρ)sinX被加载在ω2,2ω1+ω2和2ω1-ω2等频率信号中,相关项sin(2ρ)sinX被加载在ω1、2ω2+ω1和2ω2-ω1等频率信号中。通过求解双弹光级联差频调制的不同频率成分,便能够实现应力延迟量和快轴方位角的同时测量。在本方案中,采用数字锁相技术通过FPGA控制AD采样频率,将AD转换后的检测光强数字信号序列输入FPGA中[15-17],同时解调出两个PEM的基频信号幅值Vω1和Vω2,和差频信号幅值Vω2-ω1:
为了数据求解方便,将两个PEM的基频信号幅值(和)和差频信号幅值求比值,定义两个通道的比值为RI和RII:
利用上述比值,同时求解出待测样品的应力延迟量R与快轴方位角ρ:
本文方案通过双弹光级联差频调制的偏振分析系统单次测量便能同时实现应力延迟量R与快轴方位角ρ测量,结合电动平移台推扫样品便可实现样品整个通光面上的应力二维空间分布测量。
3 实 验
按照原理图1搭建的系统装置如图2所示。应力双折射二维分布测量系统装置的仪器结构尺寸为850×1 750×650 mm(宽×高×深),自上而下主要分为样品测量室和信号处理室。检测激光选用杭州新势力光电技术有限公司NewOpto-633-2-P型氦氖激光器,波长632.8 nm,光功率2 mW,光斑大小为2 mm;起偏器和检偏器选用格兰泰勒偏振棱镜,消光比优于105∶1;PEM1和PEM2为本文自行研制的单驱动八角对称状结构PEM,压电驱动器为压电石英晶体,通光晶体选用熔融石英晶体。PEM1和PEM2的熔融石英晶体尺寸分别为60×60×16 mm和54.2×54.2×16 mm,加工装调好的两个PEM谐振频率分别为44.91 kHz和49.95 kHz。电动平移台为武汉红星扬科技有限公司生产的精密二维电动平移台,XY行程150×150 mm,最大扫描速度6 mm/s,定位精度50 μm。探测器选用大恒光电DH-GDT-D020V硅光电探测器。PEM驱动控制及数据处理模块是以紫光同创PGL25G-6IMBG324型 FPGA为核心加工制作。FPGA的DDS模块提供驱动方波信号经电感电容(LC)谐振放大电路放大后驱动PEM工作。调制光信号经光电探测器探测,采用12位高精度ADC转换后输入FPGA数字锁相数据处理模块,同时完成两个基频信号幅值和差频信号幅值的数据处理[15-17]。

图2 系统装置图Fig.2 System device diagram
如图2所示系统装置,检测激光、起偏器、PEM1和二维电动平移台构成系统装置的样品测量室,PEM2、检偏器探测器和控制及数据处理模块构成系统装置的信号处理室,系统装置中的电脑上位机在Windows平台基于Visual Studio编写,主要包括PEM驱动控制,平移台控制和数据处理与显示等模块。
3.1 PEM相位调制幅值设置及系统初始偏移值定标
PEM是一类谐振光机电器件,其相位调制幅值与驱动电压成正比,相位调制幅值可通过驱动电压进行精确控制[11]。结合第2节的理论分析,由式(8)和式(9)能够看出,为了实现调制信号中基频信号幅值Vω1和Vω2,和差频信号幅值较大,来获得较高的信号数据处理信噪比,本文合理设置PEM相位调制幅值使第0阶和第1阶贝塞尔级数J0和J1均取较大值。贝塞尔级数随PEM相位调制幅值变化规律如图3所示。
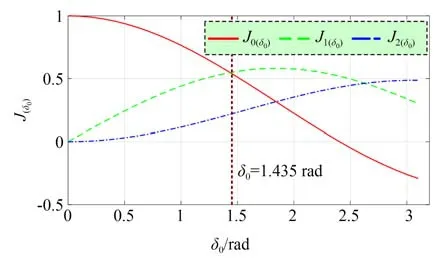
图3 贝塞尔级数Fig.3 Bessel series
依据图3可知,将两个PEM的相位调制幅值δ10和δ20设置在1.435 rad附近时,第1阶贝塞尔级数J0和J1同时取到较大值。达到该相位调制幅值,两个弹光调制器的驱动电压分别设置为185 V和190 V。
首先,不放置任何样品时,检测光信号受到两个弹光调制器调制,将调制光强信号进行数字锁相数据处理,完成系统初始值定标。数字锁相周期设置为差频信号ω2-ω1=5.04 kHz的1 008个周期, 每间隔200 ms测量一个数据点,提取的基频信号幅值和,和差频信号幅值记录如图4所示。
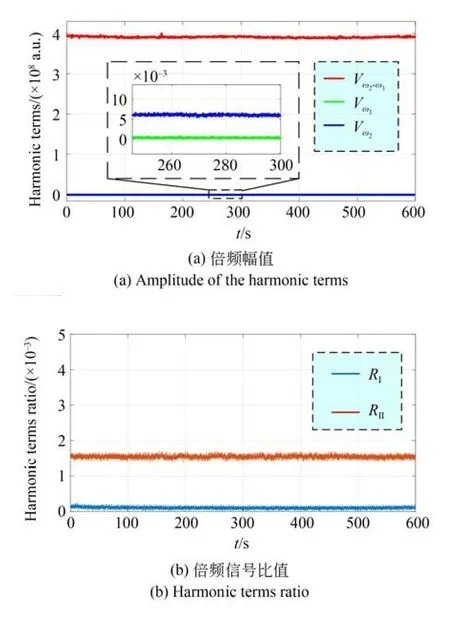
图4 调制光信号数字锁相结果Fig.4 Digital phase lock result of modulation light signals
不放置任何样品时,数字锁相获取的差频信号幅值(=3.910×108a.u.)远大于两个弹光调制的基频信号幅值(=0.425×105a.u.)和Vω(2=6.039×105a.u.),并且计算获得两个基频信号与差频信号的比值较小=0.109×10-3和=1.545×10-3。实际上,无样品时,两个比值应趋近于0,造成上述情况主要是两个PEM的自身存在微小剩余双折射造成的,但本文优选PEM搭建的测试系统在无样品时,基频信号与差频信号的比值较小,不超过10-3量级。然而,为了能够实现高精度的波片参数测量,本文将上述两个非零比值视为系统初始偏移值,在实际测量时,获得的信号比值都需要减去系统初始偏移值,尽可能减小或消除系统测量误差。
3.2 采用波片进行测量精度和重复性测试
为了确定本文方案的测量精度和重复性,论文首先选用一个632.8 nm波长的1/4波片样品,测试过程中实验室的温度设置为23 ℃,整个实验过程实验室温度波动不超过0.1 ℃。1/4波片选用北京大恒光电的GCL-060402胶合石英零级波片,延迟精度λ/300。波片裸片为1英寸,安装在大恒光电GCM-1109M可旋转镜架中,角度旋转精度5′,光学套件夹持后有效通光孔径为Φ22 mm。
首先将波片放置在平移台中部位置,让检测激光通过波片的中心位置,波片快轴方位角旋转调节至22.5°方位上。数字锁相获得的信号幅值记录如图5所示。
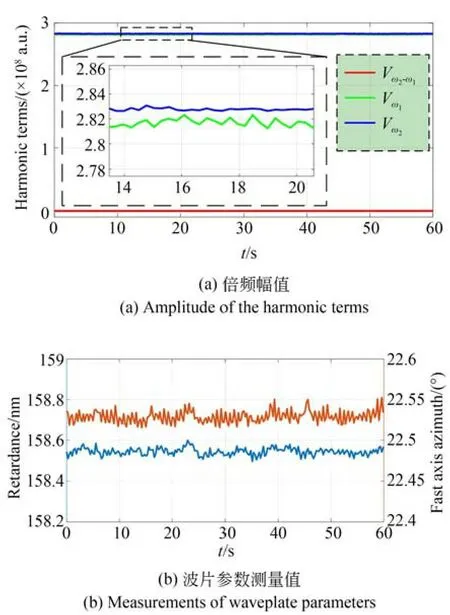
图5 1/4波片测试结果Fig.5 Measurement results of 1/4 waveplate
图5(a)可以看出,差频信号幅值几乎为0,基频信号幅值和接近。将数字锁相获得的信号幅值连同贝塞尔级数带入式(8)和式(9),进一步求解获得波片的延迟量和快轴方位角两个参数,如图5(b)。测试记录约1 min,约200个测试数据点,测量结果显示,波片的快轴方位角均值为θˉ=22.53°,标准偏差为σθ=0.01°,波片的延迟量均值为ϕˉ=158.54 nm,标准偏差为σϕ=0.02 nm,表明本文测量系统具有较好的重复性。
为了进一步实现波片在整个通光孔径的参数测量,启动精密二维电动平移台以2 mm间隔扫描26×26 mm区域。测量获得632.8 nm的1/4波片在整个通光孔径的波片参数,如图6中所示,整个测量区域耗时约1 min。为了直观显示,扫描的整个通光区域,每个空间位置的延迟量参数大小用颜色图例表示,快轴方位角直接在每个扫描图像位置以直线方位画出。
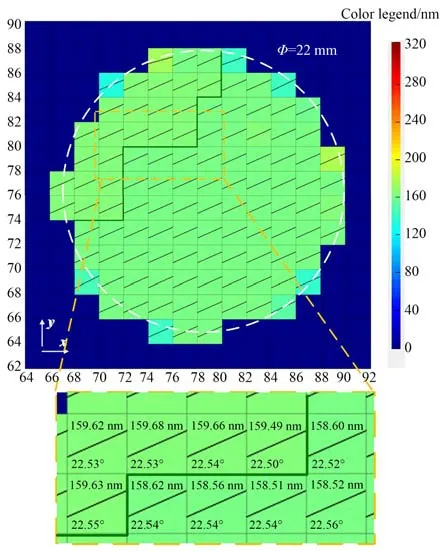
图6 1/4波片在整个通光孔径的波片参数测量结果Fig.6 Measurement results of the 1/4 waveplate over the whole optical aperture
由图6测试结果显示,延迟量整体分布在158 nm到159 nm附近。在波片的左上方区域,波片的延迟量值偏大,将扫描结果部分区域进一步放大,如图6所示。但在扫描区域边缘出现异常值数据点,主要是检测激光被旋转镜架边缘遮挡或反射造成测量误差。由实验结果能够看出,除了边缘异常数据点,整个通光孔径上波片延迟量值分布158.50~159.68 nm,快轴方位角分布在22.50°~22.56°。波片样品在整个通光孔径内延迟量参数和快轴方位角一致性较好,波片延迟量值最大偏差小2 nm,满足生产厂商延迟精度λ/300(约2.1 nm@λ=632.8 nm)的出厂要求。
3.3 应力双折射分布测量实验
为了进一步验证本文方案的应力双折射二维分布测量能力,样品选用一块双面抛光的BK7玻璃样品,样品的尺寸为150×150 mm,厚度为10 mm。玻璃样品放置在系统的样品夹持夹具上。初始时检测激光从样品中心通过。实验中选择扫描玻璃样品中部50×50 mm区域的应力双折射分布情况如图7(a)所示。应力双折射分布测量的实验结果如图7(b)所示。
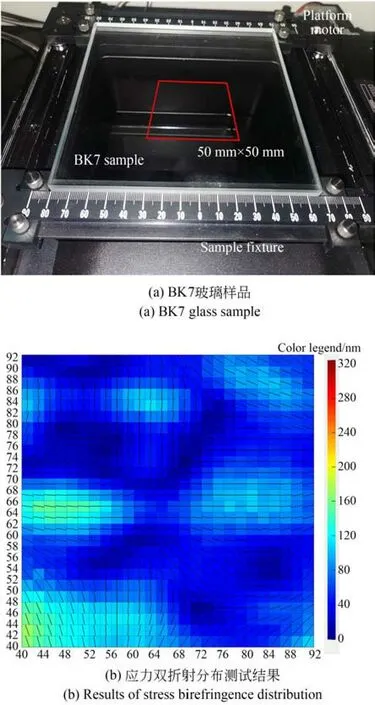
图7 BK7玻璃样品的应力双折射二维分布测试结果Fig.7 Stress birefringence two-dimensional distribution of BK7 glass sample
由实验结果能够看出,玻璃样品的应力双折射并不是均匀分布的。在测量区域的左下部分应力双折射值较大,并且存在最大应力双折射延迟量值为159.98 nm,考虑样品厚度10 mm。待测BK7玻璃样品的应力双折射不超过159.98 nm/cm。且大部分区域应力双折射延迟量值分布在80 nm以内,有的区域应力双折射值非常小,接近于0。
由图7实验结果还能看出,应力双折射的快轴方位角也不是均匀朝向分布,进一步说明BK7玻璃样品中的应力并非均匀分布。实际上,玻璃样品中的应力双折射主要来源于玻璃生长退火的内应力,和后期切割和抛磨造成的残余应力。由实验结果能够看出,本文方案可为玻璃、晶体等光学材料或光学元件应力评估,提供很好的测量评估方法和装置。
4 结 论
本文开展了基于双PEM级联差频调制的应力双折射测量研究。两个弹光调制器工作在不同的谐振频率下,构成差频调制偏振分析测量系统。样品应力双折射的延迟量和快轴方位角信息被加载到弹光调制信号中,结合数字锁相技术,同时完成双PEM级联差频调制的差频信号和基频信号解调,并同时求解出应力双折射延迟量和快轴方位角。结合二维电动平移台推扫样品,实现了样品应力双折射二维空间分布测量。论文按照原理分析研制了测试系统装置,完成了系统初始偏移值定标实验,有效地消除了PEM自身微小剩余双折射的影响;采用波片完成了测量系统测量精度和重复性测试;并完成了BK7玻璃样品的应力双折射二维分布测试,其结果表明该系统的快轴方位角标准偏差为σθ=0.01°,延迟量的标准偏差为σϕ=0.02 nm,表明本文测量系统具有较好的稳定性和重复性。并且具备应力双折射二维分布测量能力。此外,本文方案单数据点测量时间在ms量级。本方案实现了高速、高精度和高重复度的应力双折射延迟量和快轴方位角同时测量,可为波片、玻璃或晶体等光学材料双折射测量分析和评估提供有效手段。

