浅海大孔径水平阵列差频匹配场定位研究

刘 哲，朱飞龙，杨习山

(1.中国科学院声学研究所声场声信息国家重点实验室，北京 100190；2.中国科学院大学物理学院，北京 100049)

0 引 言

常规的匹配场方法通过将接收声压与拷贝场声压进行空间相关获得模糊表面进行声源定位，其定位准确性主要依赖于模型和模型参数的准确性。这使得常规匹配场定位对于失配比较敏感[1-2]，并且失配对于定位的影响会随着信号频率、阵列孔径、声源距离的增加而增大。失配主要分为系统失配和环境失配。系统失配主要包括阵元位置失配，环境失配主要包括水体声速失配、海深失配、沉积层失配等[3]。

为解决高频时匹配场不适用的问题，Worthmann等首次提出了差频匹配场的概念[4]，通过对接收信号的差频自积处理消除高频信号的相位波动，对拷贝场进行降频处理，提高定位的稳健性，并通过仿真实验验证了在完全反射边界条件下差频声压与低频拷贝场的相似性[5]。针对差频匹配场分辨力低的缺陷，Worthmann等提出自适应的差频匹配场定位方法，对差频匹配场的性能进行改进分析[6]。Dowling等使用垂直阵列，将差频匹配场用于深海远距离目标定位，定位准确率达到90%[7]。杜竞宁分析高频环境下海底衰减对差频匹配场定位性能的影响，总结出差频匹配场在海底衰减系数较大的浅海环境中定位效果更优[8]。史文佳等利用垂直阵，通过对两个频率的模糊函数做高阶互谱处理，对互谱结果进行深度积分解决了匹配结果的周期解问题[9]。

本文将差频匹配场应用到浅海大孔径水平阵列的定位中，用简正波理论分析对比了常规匹配场和差频匹配场对失配的敏感程度。仿真和实验结果表明，相比于常规匹配场方法，差频匹配场有更好的定位稳健性，在失配占主导时定位性能优于常规匹配场。

1 基本原理

1.1 常规匹配场

根据简正波理论，声压可以近似表示为各号简正波求和的形式[10]：

其中：al为第l阶简正波的幅度；ul为第l阶简正波的水平波数；βl为衰减系数；r为声源到接收的距离。假设N个阵元均分分布在长度为L的水平直线阵列中，声源位于直线阵的端射方向，其中第n个阵元的接收声压为

其中：r0为声源到阵列第一个阵元的距离，d为阵元间距。

拷贝声压表示为

其中：uls=(1+γl)ul，γl为第l阶简正波水平波数的相对失配系数，ds=(1+δ)d，δ为阵列失配相对失配系数。为简化分析，近似认为各阵元间的声压衰减忽略不计，则后续匹配处理中带有衰减系数βl的项是只与r0和rs有关的幅度项，与失配无关，后续推导将忽略衰减项。

常规匹配场的响应表达式

式(4)中第一项为期望项，可以看出期望项的幅度项受环境和阵列失配共同影响，近似呈sinc函数分布，阵列孔径越大、频率越高，sinc函数值越小，匹配对失配越敏感。期望项的相位项只受环境失配的影响，环境失配会导致定位结果出现偏差。

考虑一个等声速波导环境，声速为1 500 m·s-1，海深100 m，假定失配系数(γl+δ)/2为0.001 5，频率为200 Hz时，期望项中第一阶简正波的幅度失配响应随阵列孔径大小的变化如图1所示。从图1中可以看出，幅度失配项随阵列孔径的增大而减小。对于大孔径阵列来说，常规匹配场对失配比较敏感。

图1 幅度失配项绝对值随阵列孔径的变化Fig.1 Variation of absolute value of amplitude mismatch term with array aperture

1.2 差频匹配场

差频匹配场最初应用于高频信号的匹配处理，其通过对接收信号进行差频自积，将得到的差频声压与低频率的归一化拷贝场声压进行匹配。频率f处第n个阵元接收声压为pn(f)，选定频率差为Δf，同时对接收信号和拷贝声场进行差频自积处理，则差频接收量表示为

差频匹配场的拷贝量为：

则差频匹配场在频率f处的匹配输出为

将式(2)、(3)、(5)、(6)代入式(7)中，得到：

通过对比式(4)和式(8)，差频匹配场将距离定位的敏感项从水平波数ul变为相邻频率水平波数的差。将失配系数γ和δ代入式(8)，当相邻频率不同阶简正波对应的水平波数失配系数相近时，式(8)可以近似为

对比式(4)和式(9)可知，与常规匹配场相比，当|ul-um(f+Δf)|＜ul时，差频匹配场的期望项在幅度和相位都对失配更不敏感，更具有稳健性。

从上述推导可以得出，差频匹配场不是简单地对应简正波之间的匹配，而是相邻频率的一簇简正波之间的匹配。使用差频拷贝量进行匹配，在不存在环境失配和系统失配时，理论上可以与差频接收量完全匹配，获得更好的定位效果。

对比式(4)和式(9)，假定在频带内简正波号总数均为N，则常规匹配场期望项与非期望项的项数之比为1/(N-1)，差频匹配场期望项与非期望项的项数之比为1/(N2-1)，当N＞1时，差频匹配场非期望项比重更大，增强了模糊表面的旁瓣和背景。此外，差频匹配场每一次匹配包含了频率f和f+Δf的噪声。以上两个因素使得差频匹配场等效于降低了信号的信噪比，因此差频匹配场对信噪比更加敏感。

2 仿真分析

在浅海环境下进行仿真，仿真环境如图2所示，水深为100 m，声速在1 520～1 540 m·s-1范围变化，所用阵列为大孔径水平阵列，阵列置于水体底部，仿真信号频率为200～250 Hz，差频匹配处理选用的频率差为5～30 Hz，间隔5 Hz选取，沉积层中的声速为1 600 m·s-1，密度为1.8 g·cm-3，声吸收系数为0.05 dB·λ-1。以频率为200 Hz为例，水平波数|ul(f)|和不同频率差Δf下水平波数差|ul(f)-ul(f+Δf)|随简正波号数变化如图3所示。从图3可以发现，在选取的频率差范围内各号简正波的水平波数差均小于水平波数，结合第1节的分析，差频匹配场应对失配更具有稳健性。

图2 仿真波导环境示意图Fig.2 Diagram of simulated waveguide environment

图3 水平波数和水平波数差随简正波号数的变化Fig.3 Variations of horizontal wavenumber and wavenumber difference with normal-mode number

假定声源与参考阵元相距22 km，声源深度为50 m，带宽内阵元信噪比为0 dB，在无参数失配时常规匹配场和差频匹配场输出的模糊表面如图4所示。两种匹配方法均准确定位到声源的位置，差频匹配场模糊表面的峰值高度略低于常规匹配场，但旁瓣和背景模糊度也更低，对峰值的分辨力更高。

图4 无失配时两种匹配方法的匹配定位结果Fig.4 Matched localization results of the two matching methods in the case of no mismatch

对存在失配时两种匹配方法的定位性能进行仿真分析。环境失配考虑声速失配情形，两种失配声速剖面如图5所示，分别为实际声速剖面右移5 m·s-1和声速为实际声速剖面平均声速并增大5 m·s-1的等声速的声速剖面。

图5 真实和失配的声速剖面Fig.5 Real and mismatched sound speed profiles

使用蒙特卡洛方法比较不同信噪比下常规匹配场和差频匹配场的定性性能，带宽内阵元信噪比从-20 dB增加到10 dB，分别进行200次蒙特卡洛实验。两种匹配方法在两种声速失配情形定位的距离均方根误差(Root Mean Square Erro, RMSE)如图6所示。

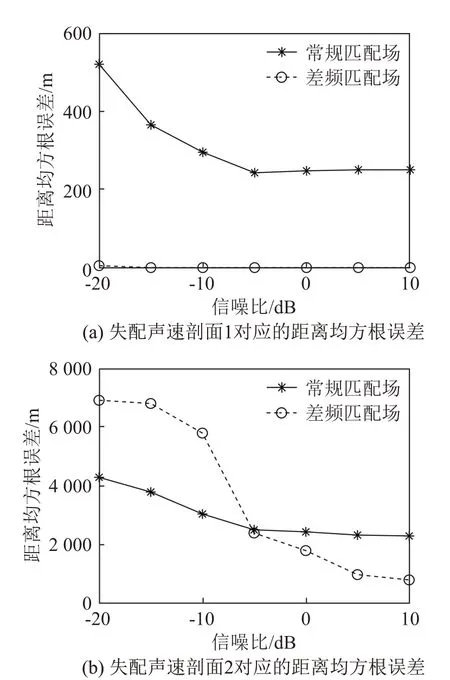
图6 水体声速剖面失配时两种匹配方法定位的距离均方根误差Fig.6 RMSE of range localization of the two matching methods in the case of mismatched water sound speed profiles

在失配声速剖面1中，声速剖面右移的情形下，常规匹配场定位出现了一定的距离误差，而差频匹配场对水平波数误差的敏感度更低，定位误差较小。在等声速的情形下，两种匹配方法都出现了较大的距离定位误差，当信噪比较高时，差频匹配场由于降低了匹配对水平波数失配的敏感度，距离定位误差更小；当信噪比较低时，差频匹配场等效降低了信噪比，因此定位效果不如常规匹配场。

考虑阵元位置失配情形，计算拷贝声场的阵元间距为真实阵元间距乘以系数0.98，带宽内阵元信噪比由-20 dB增加至10 dB，分别进行200次的蒙特卡洛实验。两种匹配方法的距离定位均方根误差如图7所示。阵元位置失配会使得接收信号的相位出现变化，降低了常规匹配场的定位性能，使得常规匹配场的距离定位误差较大；差频匹配场通过信号的差频自积抵消了相位波动，对阵元位置失配的敏感度较低，定位误差较小，定位稳性更好。

图7 阵元位置失配时两种匹配方法的定位距离均方根误差Fig.7 RMSE of range localization of the two matching methods in the case of mismatched array element positions

3 实验验证

利用浅海大孔径水平阵列实验数据对差频匹配场定位性能进行验证。实验的波导环境和水体声速剖面如图8所示，沉积层相关参数同仿真波导环境相同。实验中，一条长约500 m的水平线列阵置于海底表面，一艘水面船在端射方向由远及近驶向接收阵。两种匹配方法在不同时刻的距离和深度定位的实验结果如图9所示，处理过程中使用的信号频段为200～250 Hz，差频匹配场使用的频率差范围是5～50 Hz，间隔5 Hz选取。

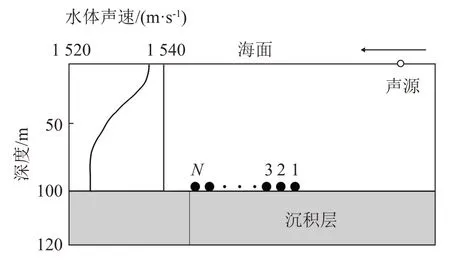
图8 实验波导环境示意图Fig.8 Diagram of experimental waveguide environment

图9 两种匹配方法距离和深度定位的实验结果Fig.9 Experimental results of distance and depth localization of the two matching methods

从图9中可以观察到，在30 min以后，声源的水平距离小于15 km，差频匹配场深度和距离结果都更加准确和稳定，而常规匹配场距离和深度定位异常点较多，只有少部分的定位结果相对准确；在前30 min，声源的水平距离大于15 km，差频匹配场定位性能开始下降，绝大部分距离定位结果都错误地定位在了周期解的位置，在声源水平距离大于22 km时甚至出现较多距离和深度定位异常点，而常规匹配场的距离和深度结果变得比较稳定。这主要是因为距离较近时，对于孔径较大的水平线列阵，平面波假设存在较大的失配，导致常规匹配场在近距离定位结果较差而在距离较远时定位结果更好，同时由于受到其他环境参数失配的影响，在前20 min，常规匹配场的定位误差随着声源距离的增加而增大；对于差频匹配场来说，由于差频匹配场对阵元位置失配敏感性更低，在近距离存在较大阵列失配时定位结果与真实值依然吻合较好，但在距离较远时，接收信号信噪比降低，又由于差频匹配场等效降低了信噪比，从而导致定位结果变差。

4 结 论

本文将差频匹配场应用到浅海大孔径水平阵列定位中，利用简正波理论进行分析对比。结果表明，差频匹配场通过差频自积处理降低了匹配结果幅度项和相位项对环境失配和阵型失配的敏感度，提高了匹配结果的稳健性。

差频匹配场非期望项展开项项数占比更高，同时匹配量包含了两个频率的噪声，等效于降低了常规匹配场的信噪比，对信噪比更加敏感。仿真和实验结果表明，在失配起主要作用时，差频匹配场能够提升常规匹配场的定位效果，定位稳健性更好，而在信噪比起主要作用时，差频自积处理反而会降低常规匹配场的最大匹配距离。关于差频匹配场非期望项对声场匹配的具体影响以及如何减弱其负面影响还有待进一步研究。