基于卷积神经网络和Transformer网络的鸟声识别

王基豪，周晓彦，李大鹏，韩智超，王丽丽

(南京信息工程大学电子与信息工程学院，江苏南京 210044)

0 引 言

鸟类作为生态系统中的重要组成部分，分布广泛且对环境变化敏感，多数学者将鸟类作为监测环境变化的指示物种[1-2]，因此对鸟类物种的监测、识别及分类具有重要意义。目前识别鸟类物种的主要方式有两种，分别是对鸟类物种外形特征的识别以及对鸟鸣声的识别，在实际监测中，由于鸟类形态监测存在成本高、范围限制大、效率低等问题[3]，使得鸟鸣声监测成为当前的主流监测方向。随着信号处理和声音识别技术的逐渐成熟，1996年Anderson等[4]利用模板匹配的方法首次实现了对靛蓝彩鹀和斑胸草雀两种鸟鸣声的识别。之后国内外学者围绕基于鸟鸣声的鸟类识别问题，通过手工提取特征、机器学习等方法展开了大量的研究，但对识别效果的提升一直比较有限。

随着深度学习的发展，国内外部分研究表明深度神经网络如卷积神经网络(Convolutional Neural Network, CNN)[5]、卷积循环神经网络(Convolutional Recurrent Neural Network, CRNN)[6]、长短期记忆网络(Long Short-Term Memory, LSTM)[7]等在鸟声识别中能提取更有价值、更丰富的特征信息。邱志斌等[8]将梅尔语谱图输入到24层的自搭建CNN模型中，利用微调网络参数在包含40类鸟鸣声的数据集中能达到96.1%的识别准确率。Takahashi等[9]在原有VGGNet卷积神经网络的基础上进行改进用于鸟声识别，结合数据增强算法解决了过拟合问题，对Freesound数据库中的鸟类进行识别实验，识别准确率较改进前提高了16个百分点。Adavanne等[10]在卷积神经网络和循环神经网络(Recurrent Neural Network, RNN)的基础上提出了卷积循环神经网络，该方法提取了主频和对数梅尔频带能量声学特征，在三个独立数据集上测试获得了95.5%的识别准确率。冯郁茜[11]提出了双模态特征融合鸟类物种识别方法，通过卷积神经网络与长短时记忆网络的级联结构，融合鸟声的时频域特征，完成对鸟声识别算法的优化，在6种鸟类识别中获得了93.9%的平均识别准确率。但文献[8-10]只使用了单一特征，并且对于某些关联性不强的数据不能获取更为全面的特征，存在一定的局限性。

本文重点关注鸟鸣声信号特征的多样性，通过短时傅里叶变换(Short Time Fourier Transform,STFT)获取包含时频域特征信息的鸟声语谱图，以及通过对原始音频信号计算得到梅尔频率倒谱系数(Mel Frequency Cepstrum Coefficient, MFCC)静态分量、MFCC一阶差分和二阶差分组成的混合特征向量。本文受文献[11]启发，提取了不同鸟声音频特征后利用双通道网络级联特征，其中一条通道利用卷积神经网络具有的平移不变性，对三维语谱图局部特征信息进行提取交互，得到局部细粒度频谱特征，同时另外一条通道利用Transformer网络结构的多头注意力机制，完成对MFCC混合特征向量的提取，得到兼顾上下文的全局序列特征，最后将两条通道的特征融合到一起，增加每一个特征的信息量以提高鸟声识别的准确率。

1 鸟声特征提取网络结构

本文提出的鸟声识别算法网络整体由两个分支组成，两个分支为并行关系，各自同时进行计算处理。上部分支首先对输入的原始音频信号进行预加重、分帧加窗等预处理操作后得到STFT三维语谱图；然后输入到卷积神经网络(CNN)中提取局部频域特征；最后通过线性层得到大小为Ncls×C1的二维矩阵特征集，其中Ncls为识别鸟类物种数目，C1为上部分支输出特征向量维度大小。下部分支首先对输入的原始音频信号进行预加重、分帧加窗等预处理操作后计算得到MFCC以及对应的一阶差分、二阶差分特征，将其拼接得到F×C2维的梅尔特征集，随后对特征集嵌入位置编码，以时序排列的方式输入Transformer编码器网络中，通过多头注意力(Multi-Head Attention, MHA)模块并行处理多组特征向量，得到兼顾上下文的全局序列特征，再通过多层感知机(Multi-Layer Perceptron, MLP)完成对输出结果的优化，最后通过线性层得到Ncls×C2维的二维特征集矩阵，其中F为梅尔特征向量维度大小，C2为下部分支输出特征向量维度大小，在这里表现为原始音频信号的输入帧数。将两条分支的特征集进行拼接融合得到更丰富的特征信息后，通过Softmax函数得到最终的预测结果。鸟声识别整体网络结构图如图1所示。

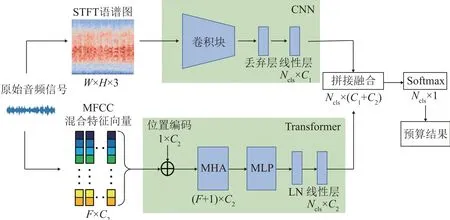
图1 鸟声识别整体网络结构示意图Fig.1 Schematic diagram of the general network structure of bird sound recognition

1.1 特征提取

1.1.1 STFT语谱图

对于获取的原始鸟声音频信号来说，每一帧内的鸟声频谱可以看作是不变的，但是这种看作不变的短时频谱只能用于反映鸟声鸣叫时的静态特性。为了能反映出鸟声信号的动态频率特性，实现对非平稳时变信号的分析，采用短时傅里叶变换生成STFT语谱图[12]。对于一个连续时间信号x(t)，其连续时间内的STFT表达式为

式中：S(ω，τ)是关于ω和τ的二维函数，w(t-τ)是时移长度为τ的窗函数。从本质上来看，STFT是对傅里叶变换(Fourier Transorm, FT)进行加窗操作，对每一次窗函数中的信号分帧进行单独处理。但实际中由于计算机只能处理离散信号，所以还需要对连续时间信号的STFT中每一帧信号的傅里叶变换用离散傅里叶变换(Discrete Fourier Transorm, DFT)代替。对于输入的离散信号x(n)，其对应的离散STFT表达式为

式中：X(l，k)是一个关于l和k的二维函数，l表示帧平移量，k表示当前谱线数，N和n分别表示总采样点数以及当前第n帧。利用幅度变化关于时间与频率的关系以及能量大小关于时间与频率的关系，还可以推导出：

式中：S(l，k)为功率谱，是能量关于时间与频率的二维函数，根据式(3)中关于X(l，k)的二维函数关系，可以绘制对应的STFT语谱图，利用图像来获取所需的三维信息，横轴为时间，纵轴为频率，颜色的深浅表示能量的大小。STFT语谱图可以清楚了解到鸟声音频随时间变化所能展现的频率以及能量的变化。

通过上述操作对原始鸟声音频信号进行处理获取STFT语谱图，窗函数采用汉宁窗，其中帧移为l=11 ms，总采样点数为N=44 100。考虑到不同种类鸟声的能量差异较大会导致生成语谱图颜色差异影响后续网络训练，为此挑选出能量最大的鸟声语谱图作为上限基准点，对所有语谱图按照式(4)标准化缩放：

为节省存储空间，将缩放后生成的语谱图压缩为256×256×3的三通道RGB图像，并以jpg格式存储。灰雁鸟声信号生成的STFT语谱图如图2所示。

1.1.2 MFCC混合特征向量

MFCC特征参数是一种在语音识别中广泛应用的特征，其更接近人耳听觉机制，可以降低原始鸟声音频中环境噪声的干扰[13]。为了获取MFCC静态特征、一阶差分和二阶差分特征组成的混合特征向量，对原始音频信号进行如下操作：

(1) 通过一阶高通滤波器进行预加重，滤波器计算公式为

其中：α取值区间为(0.9, 1)，本文取0.935。

(2) 对信号进行分帧加窗操作，窗函数选择为汉明窗，帧长为23 ms，帧移为11 ms。

(3) 对每一帧预处理后的信号进行快速傅里叶变换(Fast Fourier Transform, FFT)获取对应的频谱，再通过式(3)获得功率谱。

(4) 将功率谱输入到梅尔滤波器组中计算获得梅尔能量，其中梅尔滤波器组选用一组非均匀等高三角带通滤波器对频谱进行平滑处理，消除谐波带来的干扰[14]。设划分的三角带通滤波器为Hm(k)，则对于每一帧音频信号均存在一个对数梅尔能量函数Emel(m)，将功率谱与梅尔滤波器组计算得到的对数梅尔能量表达式为

式中：M为每组滤波器个数，本文M=40。

(5) 对经过梅尔滤波后的对数梅尔能量进行离散余弦变换(Discrete Cosine Transform, DCT)，具体求解表达式为

式中：Emfcc(n)函数中n表示当前第n帧，m取值满足式(6)中每组滤波器个数限制。创建好对应的数组标签后，可以得到MFCC静态特征。这里考虑到第0维为表征平均值，没有参考价值，且大部分能量集中在低频区，所以最后选择第1～13维共12组数据[15]。

(6) 最后为了更好体现提取鸟鸣声时域特征的上下文连续性，增加提取特征的丰富度，对MFCC静态特征计算一阶差分zid和二阶差分[16]：

式中：v=2，对获得的一阶差分和二阶差分同样取第1～13维，拼接得到二维的MFCC混合特征向量X∈RN×F，这里N表示总帧数，F=36表示提取的特征个数。

1.2 卷积神经网络(CNN)

对于从原始鸟声信号中生成的STFT语谱图来说，CNN直接采用原始图像作为输入，可以从大量图像数据中学习得到有效特征，再通过对图像的局部像素点进行感知之后在高层对信息进行共享合并，从而使网络的每一层通过共享参数来获得图像的表征信息，在加强了对语谱图局部特征提取能力的同时，又能保证网络结构本身的高度不变性。一般的CNN由输入层、卷积层、池化层、全连接层和输出层组成，本文使用ResNet50作为网络主干，考虑到输出参数量较少的同时加入了残差模块，减少了网络深度加深之后梯度消失问题的影响[17]。网络设置的输入尺寸大小为256×256，和上文中提取的语谱图大小一致；第一层卷积层之后输出大小为128×128；然后通过四组残差模块，最后通过全连接层得到大小为Ncls×2 048的二维数组，Ncls为设定的鸟声识别种类；卷积核大小设定均为3×3，池化层大小设定均为2×2×2。

1.3 Transformer网络模型

在鸟声识别中，不仅需要对每帧音频信号进行关注提取，还需要考虑每一帧信号在对应位置的重要程度。为此对于上文中通过梅尔对数转换提取获得的MFCC混合特征向量，本文加入了Transformer网络模型[18]，通过该模型所带有的多头注意力(MHA)机制，寻找定位显著性的鸟声音频表征特征。之前很多时间序列处理任务中都有加入注意力机制[19]，但却只能在每一步中只关注一个区域的特征信息，而Transformer网络模型通过多个注意力模块并行处理特征参数，既能利用注意力机制提取信息，还能加快网络的训练速度，得到兼顾上下文的全局序列特征。

Transformer网络主要由编码器和解码器两部分组成。本文主要利用Transformer网络中的的编码器部分完成对MFCC混合特征向量的提取。Transformer网络编码器部分结构如图3所示，主要由MHA和多层感知机(MLP)组成，中间加入了残差连接、层标准化(Layer Norm, LN)和Dropout层。

图3 Transformer编码器网络结构Fig.3 The structure of Transformer encoder network

对于输入的MFCC混合特征向量X∈RN×F，首先需要进行位置编码来保证音频帧按照时序顺序正常输入。本文采用正余弦位置编码，计算公式为

式中：p表示每一帧在整段信号中的绝对位置，q表示维度，d表示可输入特征向量的最大维数，目的是保证位置向量长度和输入特征向量大小一致，这里d=512，2q和2q+1用于表示位置奇偶性，对生成的位置编码与原二维特征向量进行相加操作得到新的输入向量X'∈RN×()F+1。将加入位置标记的特征向量导入到后续的MHA模块中，本文的MHA使用了注意力机制：

其中：Att(Q，K，V)函数可以看作将一个查询(query)和一系列键值(keys-values)对映射为一个输出的过程：X'×(WQ，WK，WV)→(Q，K，V)，将新的输入向量X'与权重矩阵WQ，WK，WV进行乘积映射为一个query向量和一组keys-values向量。通过计算query向量和所有keys向量的点乘，之后将结果除以则是对每个输入的音频之间相关性得分进行归一化处理，使训练时梯度保持稳定，其中dk为keys向量的维度。最后通过softmax函数将权重得分转化为0到1之间的概率分布矩阵，乘上values向量后得到最终的输出矩阵。

但是单一的注意力机制只是局限于自身内部的特征联系，交互能力有限。而对于MHA来说，通过将上述的一组权重矩阵，扩充为并行输入使用多组权重，这样可以使得模型在不同的时频位置获取信息，并通过上下文信息的交互获取更丰富的音频特征，进一步增强了注意力机制中对突出部分特征信息的利用。这里的处理公式为

其中：对于hi=Att(QWiQ，KWiK，VWiV)，映射的权重矩阵WiQ∈Rd×dk，WiK∈Rd×dk，WiV∈Rd×dv。本文中设定注意力头个数i=8，每个注意力头满足dv=di=64；通过WO作为拼接后的参数矩阵保证最后拼接得到的输出矩阵与单一注意力机制计算得到的大小基本一致。

通过MHA得到的输出矩阵后续送入前馈网络(Feed Forward Network, FFN)，这里采用MLP模型作为前馈网络的主干为，表达式为

其中：W1、W2为权重矩阵，b1、b2为偏置向量，MLP模型整体由两个线性层和一个ReLU激活函数嵌套组成，输出与前置LN层通过残差连接输入到最后一个全连接层，最终得到处理后大小为Ncls×C2的二维数组，其中Ncls为设定的鸟声识别种类，C2为总帧数，本文中C2=173。

2 实验设置与分析

2.1 鸟声数据集

为了验证所提出模型的有效性，本文选用Birdsdata[20]鸟鸣声数据集和xeno-canto[21]鸟鸣声数据集进行实验。Birdsdata是2020年由北京百鸟数据科技公司最新发布的手工标注自然声音标准数据集，在国外期刊文献中已被用于鸟声的识别检测。该数据集公开收集了共20类国内常见的鸟类鸣叫声，共计14 311份wav音频文件，且所提供的音频数据均已经过2 s标准化分割以及降噪处理。xenocanto鸟声数据集作为BirdCLEF鸟声识别竞赛的官方数据集，其数据来源于全球性野外鸟声数据库网站，具有一定的权威性。该数据集包含了44种欧亚地区且均为自然环境下录制的常见鸟类音频，时长在30 s～5 min不等且自带有环境噪声。本文需要将音频文件手动分割为2 s，并对原音频中的空白部分进行删减，最后得到共计34 703份处理好的音频文件。以上数据集采样率均为44.1 kHz，各数据集包含的鸟鸣声种类和数量如表1和2所示。

表1 Birdsdata数据集信息Table 1 The information of Birdsdata dataset

表2 xeno-canto数据集部分信息Table 2 The partial information of xeno-canto dataset

2.2 实验设置及评价标准

本文中实验部分硬件操作系统为Ubuntu 20.04，GPU型号为GTX 2080Ti，CUDA版本为10.1，网络模型的搭建全部采用Pytorch 1.8.0深度学习框架。在整体训练过程中，迭代次数(epoch)设置为100，对输入数据的单次训练步长(batch_size)设置为32，优化器采用Adam算法更新权重参数，学习率(learning_rate)采用阶梯衰减方式，初始学习率设置为10-4，之后经过总迭代数的56%和78%时，均衰减为前一级学习率的0.1倍，Dropout层设置为0.2。

本文将准确率(Accuracy)和F1-score作为评估自身模型性能和对比其他模型的评价指标。F1-score得分由精确率(Precision)和召回率(Recall)两项指标加权得到，评估公式为

其中：NTP表示正样本中分类正确样本数，NFP和NFN分别表示正、负样本中分类错误样本数。具体实验中将整体数据集按照8∶2的比例划分为训练集和测试集，然后采用五折交叉验证的方式分别进行五次实验，并记录每一次训练完后的测试结果以及最后的平均结果。

2.3 实验结果与分析

首先对本文所提方法进行实验，将数据集分为A、B、C、D、E五等份，采用五折交叉验证的方式取其中四份作为训练集，一份作为测试集(例如将A、B、C、D作为训练集，E作为测试集，以此类推)，共五组实验。在Birdsdata数据上的识别准确率评估结果如表3中所示。同时为避免实验结果存在偶然性，每组实验均在打乱训练集内部顺序的条件下重复五次，求出每组实验识别准确率的均值及标准差。

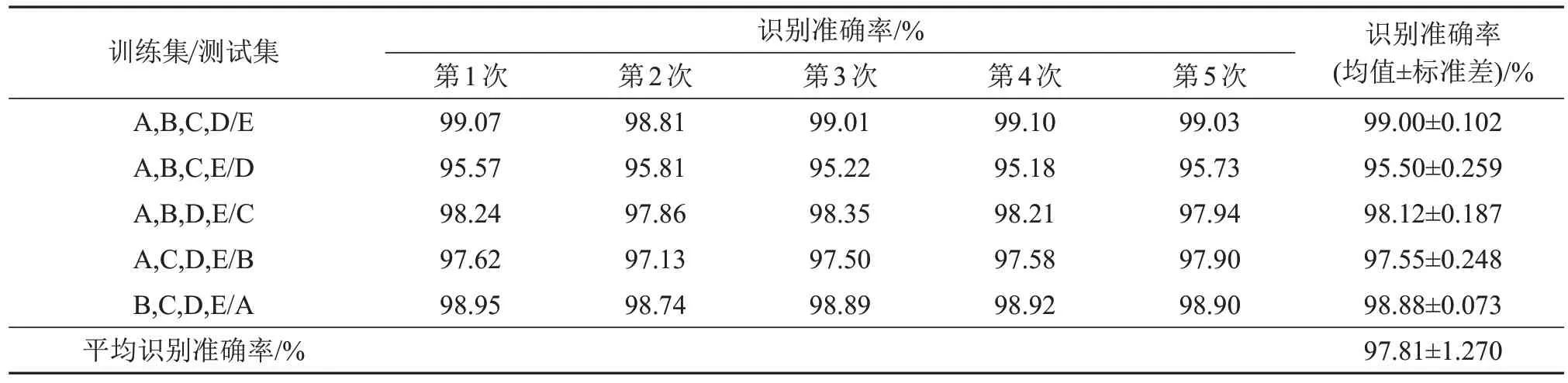
表3 在Birdsdata数据集上识别准确率评估结果Table 3 The evaluation results of recognition accuracy on Birdsdata dataset

对于Birdsdata数据集来说，当鸟声数据量较夸大、种类不是很复杂的情况下，各组样本的五次实验准确率波动不大。本文所提出的网络最高准确率为99.1%，但是在以A,B,C,E作为训练集，D作为测试集训练时整体准确率只有95.5%，说明本文考虑的对每组实验样本经过五次实验求均值和标准差之后再求整体均值的方法是有效的，能在一定程度上减小偶然对识别结果性的影响，在最后得到的识别结果中Birdsdata数据集平均准确率可以达到97.81%。

表4为在xeno-canto数据集中识别准确率的评估结果。对于xeno-canto数据集，由于鸟声数据量分布较为不均匀且种类繁多，并且音频数据中带有噪声干扰，所以本文所提出的网络整体准确率比Birdsdata数据集有所下降，且各组样本准确率波动相比于表3中结果也较为明显，例如其中最高准确率为93.25%，最低准确率为83.18%，但最后得到的识别结果中xeno-canto数据集的平均准确率也能达到89.47%。

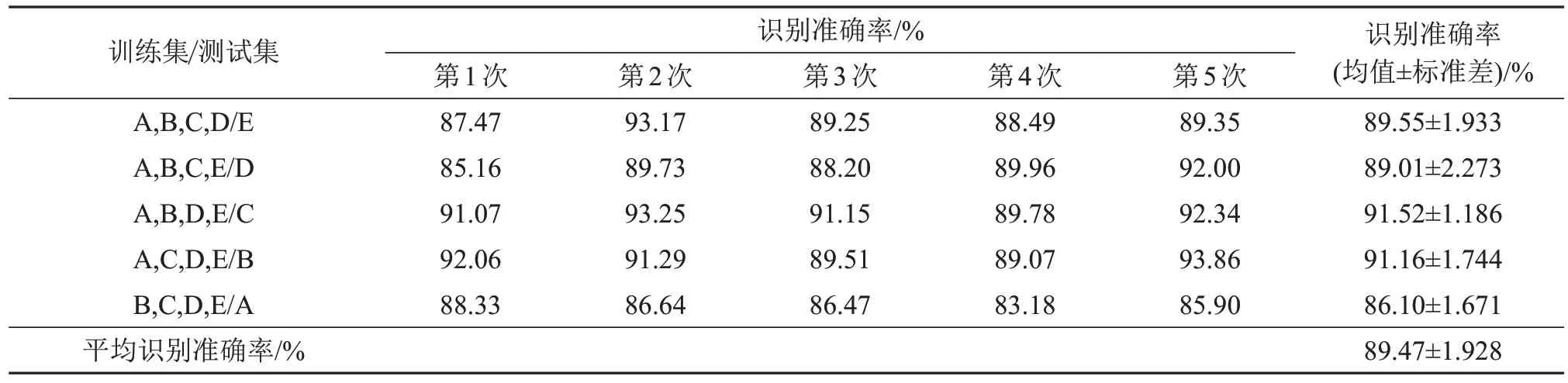
表4 在xeno-canto数据集中识别准确率评估结果Table 4 The evaluation results of recognition accuracy on xeno-canto dataset

为了体现本文所提出网络的整体收敛效果以及损失优化情况，从Birdsdata和xeno-canto两个数据集评估结果各随机抽取的一组实验过程中100次迭代后准确率以及损失函数变化的曲线图，如图4所示。由图4可以看出当学习率为10-4时，网络在大约40次迭代后就可以初步收敛；在通过阶梯学习率第一次衰减收缩之后(约55次迭代)，网络本身的识别准确率还能有约5个百分点的提升；而在学习率第二次衰减收缩之后(约80次迭代)，网络的准确率没有明显提升，也就说明网络整体已经达到全局收敛。

图4 两个鸟声数据集上训练过程中识别准确率和损失函数变化曲线Fig.4 Variation curves of the recognition accuracy and loss function in training process on the two bird sound datasets

此外，为了验证本文所提方法的有效性，将本文方法与其他方法进行了对比实验。

(1) VGGNet方法[9]：提取鸟声信号并通过STFT转化为语谱图，利用数据增强得到扩充后的数据集，输入到改进后的VGGNet中进行训练，最后通过全连接层得到鸟声分类的结果。

(2) CRNN方法[10]：对音频提取一维静态对数梅尔(log-mel)频谱值，升维处理后通过由CNN和GRU[22]组成的融合网络得到鸟声识别结果。

(3) CNN-LSTM方法[11]：通过音频得到log-Mel频谱值转化为MFCC静态分量和Mel语谱图，对MFCC静态分量进行升维操作后与语谱图数组拼接输入到CNN和LSTM级联的网络，自适应完成鸟声识别。

(4) BiLSTM-DenseNet方法[20]：将音频中提取的对数梅尔(log-Mel)频谱值转换为梅尔语谱图，输入到由双向LSTM和DesenNet并行拼接组成的神经网络中完成鸟声识别。

本文方法与上述方法进行对比，在两个数据集中不同方法下的鸟声识别准确率和F1-score得分如表5所示。

表5 在鸟声数据集上不同方法的鸟声识别结果Table 5 Bird sound recognition results of different methods on two bird sound datasets

由表5可知，本文提出的CNN+Transformer网络与上述方法相比，在两个鸟声数据集中识别准确率均有了相应的提升。在Birdsdata数据集上，CNN+Transformer网络的识别准确率可达到97.81%，F1-score得分能达到97.69%，与VGGNet、CRNN、CNN-LSTM、BiLSTM-DenseNet等方法相比准确率分别提升了4.57、3.05、2.23、5.61个百分点。在xeno-canto数据集上CNN+Transformer网络的准确率可达89.47%，F1-score得分可达到87.32%，与VGGNet、CRNN、CNN-LSTM、BiLSTM-DenseNet等方法相比准确率分别提升了12.16、3.52、1.28、10.25个百分点。

此外，为了证明本文中上下两条分支各自对特征利用的有效性，实验中对CNN(ResNet50)以STFT语谱图作为输入、对Transformer网络以MFCC混合特征向量作为输入分别进行实验。由实验结果可知，CNN(ResNet50)在Birdsdata和xenocanto数据集上的准确率分别为95.57%和83.01%，而Transformer网络在两个数据集上的准确率分别为95.91%和88.45%，均能达到和文献[11]中方法接近或更优的识别效果，可见CNN利用对局部特征的抓取能力以及Transformer网络中所用到的多头注意力机制，通过加强对重要位置的关注能在一定程度上提高识别的准确率。因此，将两种网络结构进行并联得到的CNN+Transformer网络最终能得到判别能力更强的融合特征，使得最终通过softmax分类器得到的识别效果更好。此外，可以看到在两个风格不同的数据集上，本文所提出的方法均取得了较好的识别效果，说明了CNN+Transformer网络具有较强的鲁棒性。

表6为各文献方法和本文方法的参数量对比，以及在Birdsdata数据集上训练时间(每一个epoch)的比较。

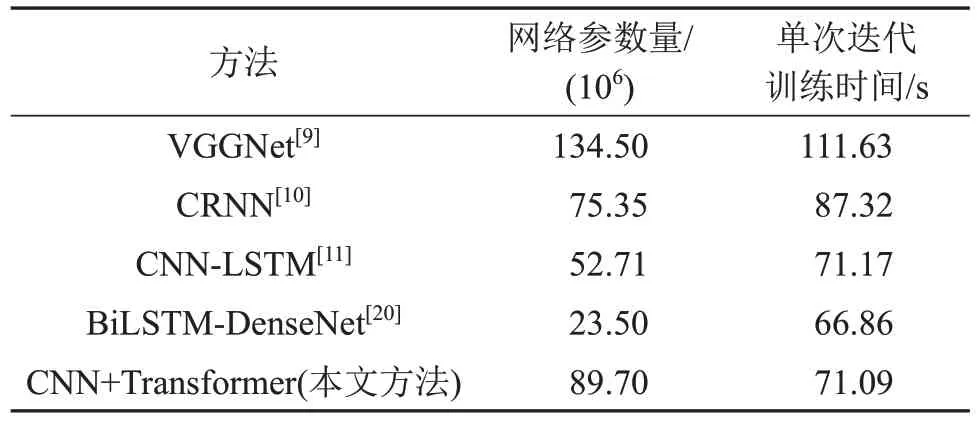
表6 不同方法网络参数量以及在Birdsdata数据集上训练时间对比Table 6 Comparison of the network parameters and training times of different methods on Birdsdata dataset

由表6可知，本文所提方法网络参数量略大于文献[10-11]的网络，但是准确率相比之下提高了2～3个百分点。此外，本文网络的训练速度仅略微小于文献[20]的方法，准确率却远高于该方法。综合两者来看，本文所提方法能基本做到在不增加较大计算量的基础上，高效利用所提取的鸟声特征，从而显著提高网络的识别准确率。

3 结 论

目前对于基于深度学习的鸟声识别研究来说，如何有效利用从音频信号中提取的各种时频域特征信息是一个值得深入研究的问题。本文提出的CNN+Transformer网络，通过对STFT语谱图以及MFCC混合特征向量的提取，利用语谱图包含的局部特征信息以及MFCC特征所具有的时频域相关信息，结合网络中CNN对局部细粒度频谱特征的关注以及Transformer解码器中多头注意力机制对全局上下文时域信息的加权计算，最后筛选出具有较强判别性的鸟声输出特征。在Birdsdata数据集和xeno-canto数据集上进行了对比实验，平均识别准确率均高于已有方法的平均识别准确率，证明了本文所提出网络模型的有效性。