采用IFIR技术的二级FRM滤波器的设计

李 杰，汪海涛

(上海船舶电子设备研究所，上海 201108)

0 引 言

水声对抗频率瞄准式干扰技术通过对声呐或鱼雷的主动探测信号进行测量分析，发射与其频率相同的干扰信号，使声呐和鱼雷无法获得正常的回波信号，从而无法对我方舰艇实施探测或跟踪。因发射功率和能源限制，对干扰信号的功率有一定的限制。

为获得更好的频率瞄准式干扰效果，需将干扰信号的频率集中在声呐或鱼雷的主动探测信号频率附近，以使能量尽量集中。该性能通过带通滤波器实现[1]。

由于目前的水声对抗器材中所用到的硬件资源有限且采用基本的FIR滤波器设计方法，导致频率瞄准滤波器过渡带较宽且带外衰减较小，进而导致干扰效果不佳。针对以上不足，本文通过设计一种高性能的带通频率响应屏蔽(Frequency Response Masking, FRM)数字滤波器来满足频率瞄准干扰工作方式的要求[2-3]。

FRM技术目前在设计窄过渡带滤波器中应用较广。该技术可设计任意带宽的滤波器，且硬件实现复杂度较低，对FRM技术的研究主要集中在结构和算法的改进上，且一般是对原型滤波器和屏蔽滤波器的复杂度进行优化设计[4-5]。

由于基本一层结构的FRM滤波器降低硬件复杂度的能力有限，当所需要的过渡带很窄，带外衰减较高时，基本一层结构FRM滤波器的硬件复杂度无法适应高性能水声对抗器材的要求，此时可通过增加FRM滤波器的层数或采用有限脉冲响应内插技术(Interpolated Finite Impulse Response, IFIR)进一步降低滤波器的复杂度。因此本文采用两层结构的FRM滤波器，并且在每一层结构中采用IFIR技术[6-10]，在满足频率瞄准式干扰带通滤波器性能要求的同时，可以进一步降低硬件实现的复杂度，满足现有水声对抗器材的硬件可实现性。

1 频率响应屏蔽技术(FRM)

频率响应屏蔽技术(FRM)是设计窄过渡带、低复杂度滤波器最常用的方法之一。由于FRM技术可以设计任意带宽的窄过渡带滤波器，且相对于传统的窄过渡带滤波器设计方法，减少了硬件乘法器的使用，进而降低了整体硬件资源的复杂度。很多学者对FRM滤波器应用与设计进行了研究，其基本二级结构如图1所示。

图1 FRM滤波器的基本二级结构Fig.1 The basic secondary structure of FRM filters

基本二级结构FRM滤波器的传输函数为

式中：(zM)为基本二级结构中的原型滤波器；Δτ=d2M为第二层结构滤波器的群延时，即原型滤波器(zM)的延时，d2为常数，与滤波器的阶数有关，M表示插值因子且设定所有层的插值因子相同，N2a表示原型滤波器的阶数。二级结构FRM滤波器的原型滤波器也采用FRM技术进行设计，将第二级的原型滤波器替换为FRM滤波器的一级结构，然后进行嵌套得到最终的二级结构。

2 IFIR-FRM滤波器

IFIR滤波器是将N阶非递归线性相位FIR滤波器的延迟单元用M个延迟单元来替换，M是插值因子，且必须是整数，进而可以产生窄过渡带滤波器。IFIR-FRM结构的滤波器，通过对原型滤波器和屏蔽滤波器进行插值来调节总体的复杂度，使总体的复杂度达到最低。通过采用IFIR滤波器达到设计低复杂度的窄过渡带滤波器的要求。

本文采用了两种常用的IFIR-FRM结构的滤波器，将其应用到两层FRM滤波器的结构中可以进一步降低复杂度。本文所采用的IFIR-FRM滤波器的结构如图2、3所示，图中所示的结构分别对屏蔽滤波器和原型滤波器进行优化。

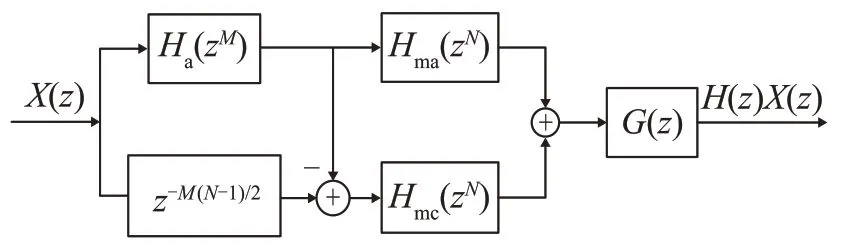
图2 第一种IFIR-FRM滤波器Fig.2 The first type of IFIR-FRM Filter

第一种IFIR-FRM滤波器的传输函数为

第二种IFIR-FRM滤波器的传输函数为

式中：Ma=M1·L，L为正整数。

两种IFIR-FRM滤波器的频率响应合成过程如图4和图5所示，图中横轴是归一化频率，纵轴是幅度。图4和图5分别表示两种IFIR-FRM滤波器频率响应合成过程的两种情况。图4对应于图2所示的结构图，图5对应于图3所示的结构图。

图3 第二种IFIR-FRM滤波器Fig.3 The second type of IFIR-FRM Filter

图4 图2所示滤波器对应的频率响应曲线图Fig.4 The frequency response curves corresponding to the IFIR-FRM filter shown in Fig.2

图5 图3所示滤波器对应的频率响应曲线图Fig.5 The frequency response curves corresponding to the IFIR-FRM filter shown in Fig.3

图4表示对屏蔽滤波器进行插值，并对屏蔽滤波器按照插值以后的频率响应进行分析，最后使用一个去除多余频带的滤波器进行滤波处理。图4中的(a)～(e)表示由插值后的原型滤波器提供过渡带的情况，其过渡带如图4中的(e)所示，图4中的(a)、(b)、(f)～(h)表示由插值后与原型滤波器互补的互补滤波器提供过渡带的情况，其过渡带如图4中的(h)所示。两种情况下滤波器的过渡带宽相同，通带宽度不同。

图4、5中M、N表示插值因子，θ和Φ分别为滤波器的通带截止频率和阻带截止频率，m为整数。图5表示在原型滤波器后级联一个滤波器，该滤波器也进行插值操作，通过系数L将两个相互级联的原型滤波器联系起来。图5中的(a)～(d)、(g)、(h)表示由插值后的原型滤波器提供过渡带的情况，其过渡带如图5中的(h)所示，图5中的(a)～(d)、(e)、(f)表示由插值后与原型滤波器互补的互补滤波器提供过渡带的情况，其过渡带如图5中的(f)所示。两种情况下滤波器的过渡带宽相同，通带宽度不同。

图5中Ma、M1表示插值因子，θ和Φ分别为滤波器的通带截止频率和阻带截止频率，m为整数。将以上参数代入式(3)、(4)对应的传输函数表达式来计算两种不同情况下各个子滤波器的截止频率，选择复杂度最优的子滤波器，使其满足低复杂度滤波器的设计要求。

3 频率瞄准滤波器的设计

本文将FRM滤波器的二层结构和两种IFIRFRM滤波器结构相结合，对每一层的复杂度都进行优化，使得在现有硬件资源条件下，进一步降低整体的复杂度。由于频率瞄准技术所需要的滤波器是带通滤波器，本文通过低通滤波器来设计所要求的带通滤波器，其结构如图6所示。图6中所示的结构是结合两种IFIR滤波器结构进行设计的，同时对原型滤波器和屏蔽滤波器进行优化，使复杂度进一步降低。由于上述结构对于带宽较宽的滤波器具有较低的复杂度，考虑到工程实际的需要，本文一些特殊带宽以及中心频率的滤波器进行了研究，由于插值因子是整数，当确定了采样频率以及中心频率等指标时，可以得到满足要求的滤波器。所以对于一些带宽较窄的滤波器，上述的二层结构可以不考虑第二层的互补滤波器，只考虑第二层的原型滤波器，这样可以在满足工程实践要求的同时进一步降低复杂度，其简化结构如图7所示。

图6 改进结构的二层FRM滤波器结构图Fig.6 Block diagram of the two-stage FRM filter with an improved structure

图7 简化的改进结构二层FRM滤波器结构图Fig.7 Block diagram of the two-stage FRM filter with a simplified improved structure

改进结构的二层FRM滤波器系统函数表达式分别为

4 设计实例

本文使用雷米兹(Remez)算法来设计FRM滤波器中所用到的原型滤波器以及屏蔽滤波器[2]。采用图7所示的简化结构的二层FRM滤波器进行带通滤波器的设计，并使用此滤波器对随机白噪声进行滤波，截取出指定通带内的噪声，观察其滤波效果。

为满足工程设计的需要，本文设计实例设计的指标比较苛刻，假设滤波器的中心频率为25 kHz，带宽为1 kHz，过渡带宽为30 Hz，通带纹波与阻带纹波分别为0.1 dB和65 dB，在满足奈奎斯特采样定理要求的条件下，选择采样频率为100 kHz，并采用简化结构的二层FRM滤波器使复杂度降低很多。简化结构的二层FRM滤波器的仿真结果如图8所示。

图8 简化改进结构的二层FRM滤波器仿真结果Fig.8 Simulation results of the two-stage FRM filter with a simplified improved structure

可以看出所设计的滤波器对随机噪声进行滤波，得到的噪声过渡带很窄，带外抑制很高，有效降低了带外干扰对所需要截取信号的影响，满足瞄频干扰工作方式的要求。同时由于所采用简化结构的特性，有效降低了复杂度，进而减少了硬件实现所需乘法器的数量。选择最优插值因子进行设计，本文所采用的结构需要的阶数为143。各插值因子为Ma=16(L=2)，M1=8，N=2，Md=7，M2=4，式中Md为第二层原型滤波器第一次插值的插值因子。

本文选择切比雪夫逼近法和图3所示结构的IFIR-FRM滤波器进行对比设计。目前常用的FIR滤波器设计的最优方法是切比雪夫逼近法。采用该方法设计具有相同性能的FIR滤波器，通过使用Matlab中的Filter Design Analysis Tool工具箱设计实现，其结果如图9所示，滤波器的阶数为9 561。

图9 切比雪夫逼近法设计的滤波器仿真结果Fig.9 Simulation results of the filter designed with Chebyshev approximation

采用图3所示结构的IFIR-FRM滤波器进行设计，当使用最优的插值因子时，滤波器阶数为274。其仿真结果如图10所示。

图10 基本一级结构IFIR-FRM滤波器仿真结果Fig.10 Simulation results of the basic primary structure of IFIR-FRM filter

由图8～10可以看出，性能相同时，本文的结构比传统等波纹切比雪夫逼近法设计的滤波器复杂度降低了98.5%，比基本IFIR-FRM结构设计的滤波器复杂度降低了47.8%。

本文的结构采用的插值因子分别为Ma=39(L=3)，M1=13，N=3，Md=4，M2=4时，此时滤波器的阶数为167，比传统等波纹切比雪夫逼近法设计的滤波器复杂度降低了约98.25%。但与使用最优插值因子的滤波器相比，复杂度高约14.4%。由此可见本文提出的结构在降低复杂度即降低硬件实现所需乘法器的数量方面有显著提高，同时也满足频率瞄准技术的性能要求。

5 结 论

根据以上的仿真结果可以看出，采用本文的结构在性能相同的情况下，可以有效降低滤波器设计的复杂度，减少乘法器的数量，进而减少了对所需硬件资源的需求。本文将IFIR-FRM滤波器用于FRM滤波器中，并采用了二层的结构来进一步降低整体的复杂度。通过上述实例分析可知，采用改进结构的二层FRM滤波器，可以实现适用于水声对抗频率瞄准式干扰方式的滤波器，在满足水声对抗频率瞄准式干扰正常工作的前提条件下，进一步提高对声呐和鱼雷的干扰性能，进而增强在水声对抗中的优势。