线偏振光通过多个任意厚度波片的偏振态

任树锋，王秀霞

（菏泽学院物理系，菏泽274015）

线偏振光通过多个任意厚度波片的偏振态

任树锋，王秀霞

（菏泽学院物理系，菏泽274015）

为了研究线偏振光通过多个任意厚度波片后的偏振态，利用线偏振光叠加的方法，对两个晶体光轴夹角为45°的不同厚度波片计算了透射的两个正交线偏振光的强度和相位差，由此得到叠加后的偏振态及透射光总强度，并分析了它们随波片延迟量、入射光方位角的变化关系。结果表明，透射光的偏振态由后面波片的延迟量决定，强度由前面波片的延迟量和入射线偏振光方位角决定，同时说明正反向使用时，透射光的偏振态和强度一般不同。该研究结果可用于类似结构退偏器（如Lyot退偏器）的分析。

光学器件；波片；偏振态；相位差；线偏振光

引 言

光波是横波，其光矢量在与传播方向垂直的平面内分布的不对称性称为偏振，相应的各种不同的振动状态即偏振态。光的偏振特性在光学技术及科学实验研究中有着广泛应用，因而偏振态的分析［1-7］成为光学的重要内容。波片是由双折射晶片制作而成的延迟器件，一般可以将垂直入射的线偏振光分解为振动方向正交且具有一定的相位差的两束线偏振光。相位差的不同决定了出射光叠加后的偏振态，如通过λ／4波片后一般是椭圆偏振光，通过λ／2波片后仍为线偏振光。单独的常用波片（如λ／4波片、λ／2波片等）对入射光偏振态的作用已有较多的详细研究报道。棱镜型的偏光器件（如各种起偏器和退偏器）往往由多个任意延迟量的双折射晶片或光楔组成，因此，光通过多个具有任意延迟量（或厚度）后的偏振态分析具有重要意义。对偏振态的分析以往大多利用矩阵方法，如Jones矩阵、Mueller矩阵［8-9］，作者从偏振光基本概念出发，利用光矢量叠加的方法，分析线偏振光通过两个任意厚度的石英波片，方法简便、意义清晰。

1 光路分析

在图1中，前后两个波片平行竖直放置，厚度分别为d1，d2。前面波片的晶体光轴沿x方向，后面波片的晶体光轴在x-O-y面内与前者成45°夹角（与Lyot退偏器结构类似）。单色线偏振光垂直入射（沿z轴），振动方向与x轴夹角，即方位角为θ。线偏振光在前面波片内分解为振动方向正交的非常光和寻常光，两者传播方向一致，相位不同且相位差随波片厚度变化。这两个线偏振光进入后面波片后又分别分解为两个相位不同的非常光和寻常光。这4束透射光用e（表示非常光）和o（表示寻常光）的字母组合命名，即ee，eo，oe和oo，前后两个字母分别表示该光束在前后两个波片的偏振属性。其中，ee和oe为前面透射的两个线偏振光在后面波片分别分解得到的两个非常光，eo和oo则为它们分别分解得到的两个寻常光。两个非常光和两个寻常光分别叠加可以得到两个振动方向垂直、相位不同的线偏振光，由此可知，最终透射光一般为椭圆偏振光。

Fig.1 The optical path of linearly polarized light transmitting through two wave-plates

2 偏振态叠加分析

对石英晶体的波片，设在后面波片的出射端面oo的初相位为0，则4束透射光的初相位可表示为：

式中，λ为入射光波长，no和ne分别是石英晶体中o光和e光的主折射率。

忽略界面反射、石英吸收以及散射，参照图1的参量设置可得4束透射光的振幅：

式中，A为初始振幅。这4束光再两两叠加：ee与oe合成得到振动方向和频率不变，在后面波片中相当于非常光的线偏振光，其振幅和初相位分别用Ae，φe表示；与之类似，oo与eo合成的寻常光的振幅和初相位分别用Ao，φo表示。由（1）式～（8）式可得：

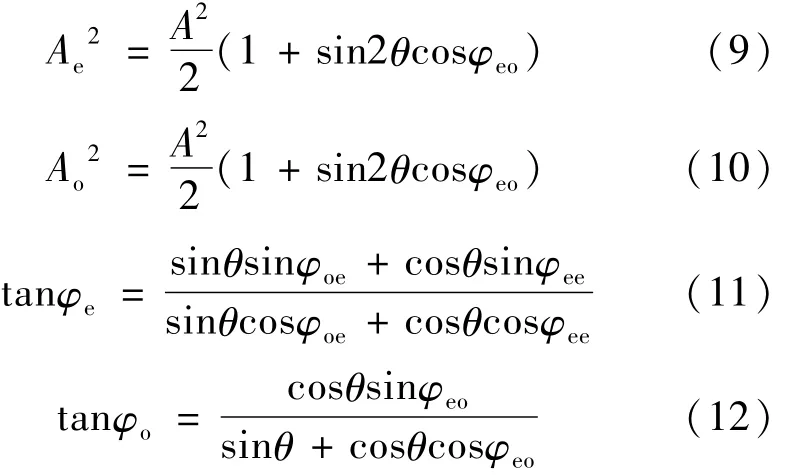
将（11）式、（12）式代入正切的差角公式：

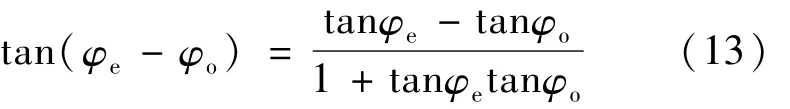
得：

其中，

通过三角函数运算，可得相位差：

由（9）式、（10）式可以计算透射光的总光强为：

由（19）式可以看到，对于确定波长的入射光，相位差由后面波片的延迟量决定；而相位差又决定透射光的偏振态，其随相位差在一个周期内的变化如图2所示。当相位差为kπ（k为整数）时，透射光为线偏振光；当相位差为（k＋1／2）π时，由（9）式、（10）式可知Ae＝Ao，因此透射光为圆偏振光；当相位差为其它值时，透射光为椭偏率不同的一般椭圆偏振光。另外，由于偏振态仅由后面波片决定，所以当反向入射时，透射光的偏振态一般与正向入射时不同这是使用时应该注意的问题。

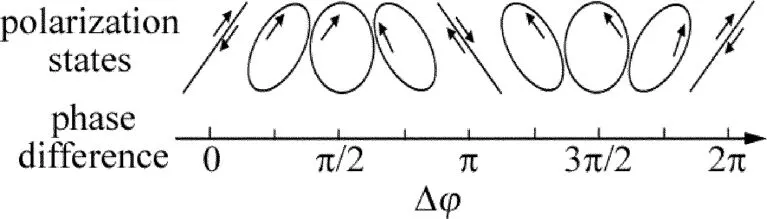
Fig.2 The polarization states of transmitted light changing with phase difference

由（20）式看到，透射光强度随前面波片延迟量决定的相位差的变化而发生周期变化，且周期与偏振态变化周期相同；入射线偏振光方位角θ决定变化幅度：θ为0°或90°时，透射光强为A2不变；θ＝45°时，透射光强变化幅度最大，在［0，2A2］内变化；θ为其它值时，透射光强变化幅度介于以上二者之间。图3为θ分别取0°，15°，45°时，透射光强随相位差变化的曲线。

Fig.3 The transmitted light intensity of different vibration azimuth angle changing with phase difference

对于多个波片（N≥3）且任意两个相邻波片晶体光轴夹角为45°的情况，前面（N－1）个波片可等效为一个波片，其透射光叠加后同样得到振动方向垂直、初相位不同的寻常光和非常光，其中非常光的振动方向与第（N－1）个波片的晶体光轴一致，即第（N－1）个波片的晶体光轴可视为前面（N－1）个波片的等效晶体光轴。因此，这两束再通过第N个波片的计算与两个波片完全相同，结论也一致。

3 实验验证

样品为一个石英晶体材料的8mm波片与λ／4波片（633nm）的组合。由于较厚波片的延迟量对入射角非常敏感，难以准确测定，所以将λ／4波片放在后面。实验光路如图4所示，激光光源的波长为633nm，后面放置相应波长的波片，可将光源近似调制为圆偏振光（减小光源主偏振面旋转的影响）。起偏棱镜的旋转可以改变入射线偏振光的方位角，而检偏棱镜的旋转可以检测透射光的偏振态。另外，由于波片对入射角很敏感，采用自准直方法调整光的垂直入射。

Fig.4 The light-path diagram of experiments

对于（20）式：去掉检偏棱镜，通过旋转起偏棱镜，可以验证透射光强随（2倍）方位角按正弦规律变化，实验曲线如图5所示。

Fig.5 The diagram of transmitted power changingwith vibration azimuth angle

对于（19）式：在仔细调整光的垂直入射（特别是λ／4波片的垂直入射），以及两波片晶体光轴夹角为45°的前提下，旋转检偏棱镜，发现透射光强变化很小，见表1。

Table1 The transmitted power changing with the rotation of the analyzer

由表1可见，随检偏棱镜的旋转，透射光强变化幅度很小，最大值与最小值的差值仅为平均强度的2.92%。由此可以判断透射光为圆偏振光，这与利用（9）式、（10）式及（19）式分析得到的结论相同。

4 结 论

利用线偏振光叠加的方法，计算分析了单色线偏振光垂直通过两个任意厚度、晶体光轴夹角为45°的波片后的偏振态和光强。理论分析表明，透射光的偏振态由后面波片的延迟量决定，强度由前面波片的延迟量和入射光方位角决定。通过实验，该结论得到一定验证。分析结果可以推广到多个波片且相邻晶体光轴夹角为45°的情况。另外，应用数学积分，还可计算分析复色光的情况；该研究可应用于具有相近结构的双折射型棱镜偏振态的分析，如Lyot退偏器［10-11］。

［1］ LIU F，LEE Ch J，CHEN JQ，et al.Ellipsometry with randomly varying polarization states［J］.Optics Express，2012，20（2）：870-878.

［2］ REN Sh F，WU F Q.Design of bireflective parallel beamsplitting polarization prism combined of iceland and glass［J］.Laser Technology，2012，36（5）：686-688（in Chinese）.

［3］ WANGW，XIE Y，XU L L.Research on change of the polarization status for the polarized light passing through quarterwave plate［J］.Journalof HuaibeiCoal Industry Teachers College，2010，31（2）：26-29（in Chinese）.

［4］ YOU Y，TONIZZO A，GILERSON A A，etal.Measurements and simulations of polarization states of underwater light in clear oceanic waters［J］.Applied Optics，2011，50（24）：4873-4893.

［5］ ZHENG G L，XU J，WANG H C，et al.Effect of polarization state on electro-optic coupling and its application to polarization rotation［J］.Applied Optics，2006，45（34）：8648-8652.

［6］ KRZYSZTOF P.Analysis of clusters and uniformity of distribution of states of polarization on the Poincarésphere［J］.Applied Optics，2005，44（21）：4533-4537.

［7］ RAJENDRA B.Halfwave retarder for all polarization states［J］.Applied Optics，1997，36（13）：2799-2801.

［8］ JIAO Sh L，TODOROVIC M，STOICA G，et al.Fiber-based polarization-sensitive mueller matrix optical coherence tomography with continuous source polarization modulation［J］.Applied Optics，2005，44（26）：5463-5467.

［9］ DO T，DONG H，SHUM P.Measurementof the complex polarization mode dispersion vector using jonesmatrix analysis［J］.Applied Optics，2007，46（6）：916-921.

［10］ REN Sh F.Study on the polarization dependence of an improved Lyot depolarizer bymeansof superposition ofmultiple beam［J］.Optical Technique，2012，39（1）：14-18（in Chinese）.

［11］ REN Sh F，WU FQ，WUW D.Depolarization performance for monochromatic light of an improved Lyot depolarizer［J］.Acta Optica Sinica，2013，33（4）：0423001（in Chinese）.

Polarization states of linearly polarized light transm itting through several wave-plates w ith arbitrary thickness

REN Shufeng，WANG Xiuxia
（Department of Physics，Heze University，Heze 274015，China）

Adopting the means of light vector superimposition，the polarization states of linearly polarized light transmitting through several wave-plateswith arbitrary thicknesswere analyzed.Taking two wave plates whose optical axes are oriented at45°as example，the polarization states and intensity of transmitted lightwere calculated.It is found that the polarization states are dependent on retardation of the back wave-plate，and the intensity is dependent on retardation of the frontwave-plate and vibration azimuth angle of incident light.Italso indicates that the characteristics are not the samewhen the two wave plates are used in forward and reverse directions.The theoretical results can be applied to the analysis of depolarizer，such as Lyot depolarizer.

optical devices；wave-plate；polarization state；phase difference；linearly polarized light

O436.3

A

10.7510／jgjs.issn.1001-3806.2014.03.024

1001-3806（2014）03-0394-04

山东省高等学校科技计划资助项目（J11LA52）；荷泽学院自然科学基金资助项目（XY13KJ04）

任树锋（1979-），男，讲师，主要研究方向为偏光器件的设计与分析。

E-mail：renshufeng7909＠163.com

2013-05-14；

2013-07-03