应用频率积分相位解调测量径向畸变

杨初平，刘建斌，谭穗妍，翁嘉文

（华南农业大学物理系，广州510642）

应用频率积分相位解调测量径向畸变

杨初平，刘建斌，谭穗妍，翁嘉文

（华南农业大学物理系，广州510642）

为了测量光学成像系统的径向畸变，采用载频条纹模板，应用瞬时频率积分法提取因径向畸变而产生的径向调制相位；推导了条纹径向调制相位与瞬时频率的关系式，并导出径向调制相位和径向畸变位移关系；采用小波频率估计提取畸变条纹径向瞬时频率，并对其进行积分获得畸变条纹的径向调制相位；应用径向调制相位和立方卷积插值算法对畸变图像进行了校正，得出了详细的理论分析和实验结果。结果表明，上述方法是可行的。

测量与计量；畸变测量；载频条纹；相位解调；径向畸变

引 言

畸变普遍存在于光学成像系统中。径向畸变测量就是获得径向畸变位移函数即畸变像点相对于无畸变像点的位移，校正畸变图像。通过设定特征点、提取特征点的畸变位移的标定模板［1-7］是目前测量径向畸变的主要方法。如果把这些特征点的灰度按正弦函数分布排列，则测量因径向畸变导致的特征点的位移将转化成测量灰度条纹径向调制相位。本文中以纵向正弦载频灰度条纹作为模板，把径向位置畸变转化为径向调制相位，采用小波频率估计提取畸变条纹径向瞬时频率并进行积分运算得到径向调制相位。与目前提取条纹调制相位都需要进行相位解包［8-14］不同，采用瞬时频率积分相位解调方法提取变形条纹调制相位方法没有产生包裹相位，因而无需经相位解包过程，便可直接得到调制相位。然后换算为径向位置畸变，实现对图像的校正。

1 图像畸变模型

畸变图像建立如图1所示的坐标系。径向畸变相对于图像中心点O具有旋转对称性，在同一圆周上的点具有相等的位置畸变。设（x0，y0），（x，y），（xd，yd）分别表示图像中心点、理想像点和对应的畸

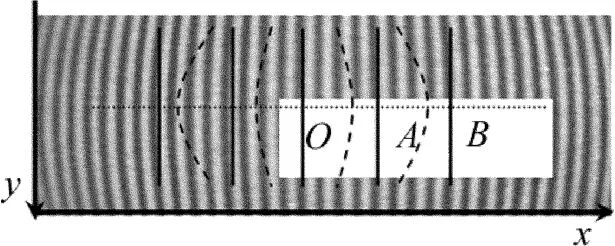
Fig.1 Diagram illustrating radial distortion of fringe patterns

式中，径向畸变位移函数T（r）是描述畸变像点相对于无畸变像点的位移，表示为：

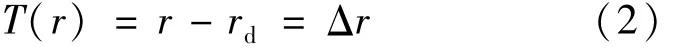
通过实验得到Δr，代入（1）式并结合灰度插值得到校正图像。

2 径向畸变相位

2.1 径向调制相位与径向瞬时频率

以条形正弦灰度模板进行成像，采集的畸变条纹和无畸变条纹的关系如图1所示，其中径向OAB经过图像中心O点。采集的无畸变条纹像的灰度可表示如下：

式中，A1（x）是背景灰度，B1（x）是正弦灰度的幅值，相位分布是（2πf0x＋φ），f0是频率，φ是初始相位。

一方面，由于畸变，采集的条形模板灰度不再是正弦分布，可表示为：

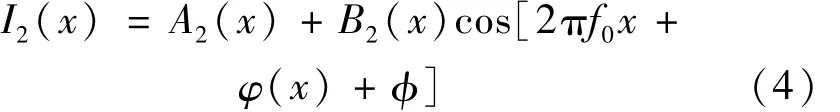
式中，相位分布是［2πf0x＋φ（x）＋φ］，不再是周期性分布，而是出现沿着径向发生变化的调制相位函数φ（x）。畸变条纹像与无畸变条纹像比较，因径向畸变产生的相位差即径向调制相位函数为：

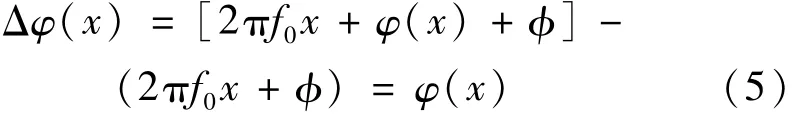
另一方面，径向畸变表现为畸变像点相对于无畸变像点的位置移动，如图1所示，径向畸变使B点移到A点，产生的径向畸变位移函数表示为Δr（x）。则径向畸变相位函数与径向畸变位移函数的关系为：

因此，只要得到径向调制相位就可以计算径向畸变位移分布。

畸变条形模板灰度分布不再是固定的频率f0，而是随着径向发生变化。畸变条形径向瞬时频率定义为：

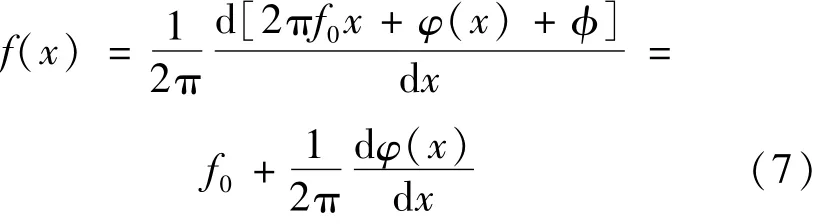
把f0移到等号左边，两边积分得：φ（x）－φ（0）＝在畸变像的中心点，畸变为0，则瞬时频率f（0）＝f0，而且φ（0）＝0。因此径向调制相位函数为：

因此，若得到瞬时频率分布f（x），则可以计算径向各个畸变点的径向调制相位。在以往的条纹调制相位解调过程中，由于采用反正切函数计算条纹每个点的调制相位，大于2π的调制相位将被折断到（－π，π）范围内，为了获得真实调制相位，需要对解调相位进行解包处理。采用瞬时频率积分不会出现相位折断，因而无需相位解包过程就能够直接计算真实的调制相位。

2.2 频率估计

条纹上各点瞬时频率的计算可以采用连续小波变换进行估计。对1维函数f（x），其连续小波变换系数Wf（a，b）定义为［11-13］：

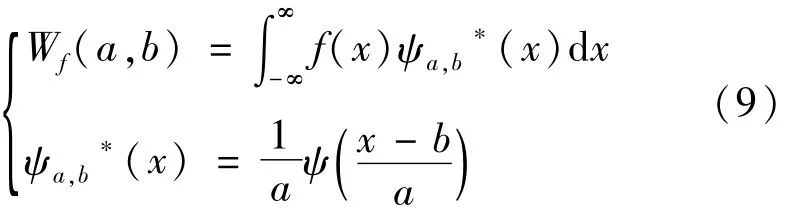
母函数ψ（x）采用Gabor小波函数［12］：

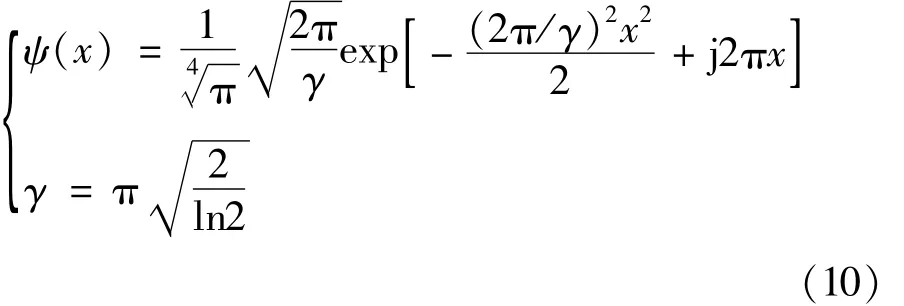
式中，ψa，b（x）为母函数经过尺度因子a伸缩和平移因子b平移后得到的小波序列，ψa，b*（x）是ψa，b（x）的共轭函数。对实信号f（x）的各个b点采用不同a值进行连续小波变换，得到一系列的小波系数Wf（a，b）。小波系数的幅值A（a，b）和相位φ（a，b）可以通过Wf（a，b）的实部Re［Wf（a，b）］和虚部Im［Wf（a，b）］分别表示为［12］：

对信号各个位置b，通过检测不同a值的小波变换系数幅值A（a，b），其中最大值所对应的尺度因子a就是最佳尺度，记为a（b），信号在b点的瞬时频率可以估计为f（b）＝1／a（b）。把变形条纹I2（x，y）过中心点O沿OAB方向的灰度分布作为f（x），按照上述过程可以提取畸变条纹径向OAB的瞬时频率分布f（x）＝1／a（x），经过瞬时频率积分得到径向调制相位函数。

3 实验结果

调整摄像机光轴垂直参考平面，然后采集图像。图2是成像系统采集的变形条纹（640pixel× 480pixel），中心点O即零畸变点位于（320，240）。图3是OAB方向的瞬时频率分布，以O为中心呈左右对称。图4是对O点右侧瞬时频率积分得到径向调制相位的原始曲线和多项式拟合曲线。按照（4）式把图4中的径向调制相位转化为径向畸变位移，采用立方卷积插值法［15］对畸变图像（见图5）进行校正，校正图像如图6所示。

Fig.2 Distorted fringe pattern

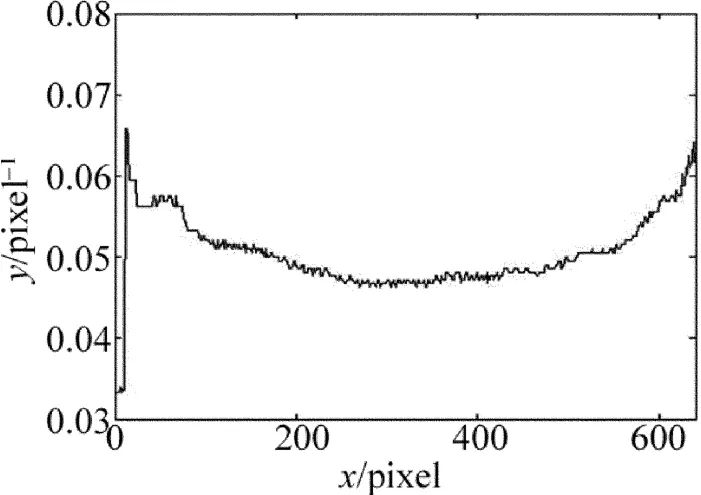
Fig.3 Local frequency along OAB

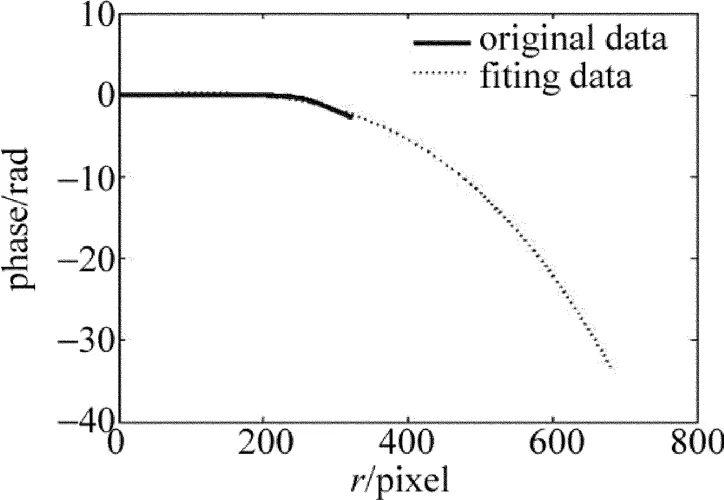
Fig.4 Modulated phase along OAB

Fig.5 Distorted image

Fig.6 Calibrated image

4 小 结

为了测量成像系统的径向畸变，以正弦灰度条纹模板作为成像对象，把径向位置畸变转化为变形条纹径向调制相位；该方法只需要采集1幅畸变条纹图像，该变形条纹不仅含有径向畸变信息，而且在畸变条纹中心点含有无畸变条纹像信息，采用小波频率估计提取径向频率并进行瞬时频率积分计算径向调制相位，实现畸变校正。

［1］ TANGW，YE D，YUAN F，et al.Independent distortion correction algorithm in vision measurement system［J］.Journal of Optoelectronics·Laser，2013，24（2）：308-315（in Chinese）.

［2］ JIN Y，MENG JB，WANG K，et al.The research of plane array camera geometric distortion correction method［J］.Microelectronics＆Computer，2011，28（10）：36-43（in Chinese）.

［3］ SU C Z，WANG E G，HAO JT，et al.Distortion correction for images in planarmetrology［J］.Optics and Precision Engineering，2011，19（1）：161-167（in Chinese）.

［4］ WU K X，DUAN M L.New method of correcting barrel distortion on latticemodel［J］.Journal of Computer Applications，2012，32（4）：1113-1115（in Chinese）.

［5］ KONG B，FANG T J.A simple and precisemethod for radial distortion calibration［J］.Journal of Image and Graphics，2004，9（4）：429-434（in Chinese）.

［6］ YU J，LIN JM，YANG JY，et al.Distortion measurement and calibration technology for CCD camera system on new target board［J］.Acta Optica Sinica，2007，27（8）：1440-1442（in Chinese）.

［7］ XUW X.The study of lens distortionmeasurementof NFOV based on star pointmethod［J］.Laser Technology，2011，35（5）：593-595（in Chinese）.

［8］ YANG Ch P，WENG JW，YANG L L，et al.Grid fringe pattern Fourier transform profilometry［J］.Laser Technology，2010，34（4）：493-496（in Chinese）.

［9］ YANG Ch P，WENG JW，WANG JW.Distortion measurement and calibration technique based on phase analysis for carrier-fringe pattern［J］.Acta Photonica Sinica，2010，39（2）：316-319（in Chinese）.

［10］ LIB，QIAN X F，LIX H，et al.Phase-unwrapping algorithm based on radial shearing principle［J］.Laser Technology，2013，37（1）：44-47（in Chinese）.

［11］ SUN J，CHENW J，SU X Y，etal.Study themeasurement range ofwavelet transform profilometry［J］.Acta Optica Sinica，2007，27（4）：647-653（in Chinese）.

［12］ ZHONG JG，WENG JW.Phase retrieval of optical fringe patterns from the ridge of a wavelet transform［J］.Optics Letters，2005，30（19）：2560-2562.

［13］ YANG Ch P，LIU Y，LIH.Radial distortion distribution in optical imagingmeasured by wavelet phase analysis［J］.Acta Optica Sinica，2012，32（9）：0912001（in Chinese）.

［14］ WANW B，SU JH，YANG L H，etal.Phase unwrapping algorism for image processing of interferogram［J］.Journal of Applied Optics，2011，32（1）：70-74（in Chinese）.

［15］ YOU Y H，ZHOU X K.Research on optimal interpolation algorithm for digital image［J］.Chinese Space Science and Technology，2005，25（3）：14-18（in Chinese）.

M easurement of radial distortion based on frequency integration phase demodulation

YANG Chuping，LIU Jianbin，TAN Suiyan，WENG Jiawen
（Department of Physics，South China Agricultural University，Guangzhou 510642，China）

Tomeasure the radial distortion in optical imaging systems，adopting the straight sinusoidal carrier-fringe pattern，the radial modulated phase resulting from radial distortion was extracted by means of instantaneous frequency integration.The formula between the instantaneous frequency and the radial modulated phase was deduced，and the conversion formula between the radial modulated phase and the radial distortion displacement was obtained.The instantaneous frequency of the distorted fringe pattern in the radial direction was calculated by using frequency estimation of Gabor wavelet transform，and integrated to obtain the radialmodulated phase.The radialmodulated phase and the cubic convolution interpolation algorithm were used to calibrate the distorted image.Experimental results demonstrate that the method is available.

measurement and metrology；distortion measurement；carrier frequency fringe pattern；phase demodulation；radial distortion

O438

A

10.7510／jgjs.issn.1001-3806.2014.03.026

1001-3806（2014）03-0402-04

国家自然科学基金资助项目（61307011）；广东省自然科学基金资助项目（9151064201000035）

杨初平（1970-），男，副教授，研究方向为光信息处理。

E-mail：yangchp＠scau.edu.cn

2013-07-09；

2013-10-08