基于涂层材料分布状态的超声-应力反演模型构建

柯庆镝 罗俊友 蒋守志 黄海鸿

1.合肥工业大学机械工业绿色设计与制造重点实验室,合肥,2300092.合肥工业大学机械工程学院,合肥,230009

0 引言

当前,增材制造技术逐渐被应用到机械制造领域中,其工艺原理主要为利用高能离子束或激光束熔化金属合金粉末或金属丝材,根据设计结构将金属粉末按照一定规律堆积在基体材料上,实现金属零件的增材制造[1]。在增材制造过程中,由于存在金属液固相变过程,导致增材涂层结构应力分布不均匀,会形成涂层结构缺陷,并可能影响到所制造零件的力学性能及可靠性,因此,在金属增材制造过程中,检测与评估成形结构的应力状态,对保障涂层结构及其零件的服役性能和可靠性具有重要意义。

针对应力状态的检测与评估问题,相关学者已利用超声[2]、磁信号[3]、涡流[4]等无损检测技术进行了研究。由于超声检测技术具有成本、探测深度及适应性等优势[5-6],因此部分研究集中于利用超声检测技术分析成形结构的应力状态。WANG等[7]推导了正交各向异性材料中的超声传播时间与主应力间的改进方程;DEMCENKO等[8]通过对刚度矩阵的改进,分析了一维多层弹性材料的超声波速与外加应力的函数关系;ZHAN等[9]基于激光超声技术获得的声弹性系数评估了钛合金焊接板中的残余应力。针对增材制造中涂层结构的声学特性,LEMLIKCHI等[10]将最大似然估计法与Levenberg-Marquardt算法结合对涂层中的超声信号进行了估计,结果表明超声波速度和信号衰减速度会随着涂层材料的硬度增大而变大。YAN等[11-12]利用瑞利波和临界折射纵波(LCR波)评估了激光熔覆层的表面应力;WANG等[13]提出了一种基于参数的等效建模方法来预测涂层结构的残余热应力场。

以上研究均是利用应力场中超声传播变化规律构建对应的应力与超声信号映射模型,进而分析各类金属结构中的应力状态的。但以上映射模型均基于所检测结构的材料声弹性系数,在增材制造成形过程中,涂层结构不同区域的成形过程并不一致,其声弹性特征也会随材料分布状态而产生变化,并直接影响其超声无损检测结果的精度与可靠性[14],而现有的针对涂层区域材料分布下声弹性特征及其对声信号传播影响的相关研究较少,因此,本文基于金属材料声弹性特征与超声信号之间的映射关系,通过分析涂层结构中材料分布状态,讨论涂层结构的声弹性特征表达,建立面向涂层结构的应力反演模型。随后,开展不同应力状态下涂层结构的超声检测实验,验证并分析所提出的涂层结构声弹性特征表达的有效性及可行性。

1 涂层结构中声弹性特征表达

1.1 超声传播及声弹性理论基础

在初始无应力状态下的固体弹性材料中,超声纵波的初始速度仅与材料性质有关,关系如下[15]:

(1)

式中,v0为零应力状态下的超声波传播速度;ρ0为初始无应力状态下固体弹性介质的密度;λ、μ均为固体弹性介质的一阶、二阶Lame常数。

应力状态下的超声纵波传播速度v与初始速度v0的关系式为

(2)

式中,k为声弹性系数;σ为应力值(正数表示拉伸应力,负数表示压缩应力)。

对于均匀分布简单一维应力的固体弹性介质,其材料不变,即声弹性系数k视为不变,则应力分布均匀,应力值σ为常数。由式(2)可知当超声传播方向与应力方向垂直或者平行时,超声波的传播时间为

(3)

式中,S0为超声波的传播路程。

由于超声纵波与应力之间方向不同,因此可将声弹性系数k分为超声传播方向与应力方向垂直时的kc和超声传播方向与应力方向平行时的kp。

1.2 涂层结构中声弹性特征分布

在金属增材制造过程中,涂层是由金属粉末以熔融、喷射等方式在基体结构上逐层堆积而成形的,可以视其为一种“自下而上”的层状结构。图1所示为等离子喷焊涂层3D激光显微组织。通过3D激光显微镜(型号:VK-X250)对试件材料表面轮廓与形状进行三维测试和定量分析,可以观察到基体材料(C45E4)和涂层材料(Cu)的涂层结构试件的结合处界面结构组织。

图1 涂层结构截面3D激光显微组织Fig.1 3D laser microstructure of coating structure section

(1)基体与涂层区域。涂层结构中,基体区域是已成形的固体金属材料,涂层区域的成形过程可看作是金属粉末的堆积及固化过程,该区域的主体材料为固化状态的金属粉末,所以基体与涂层区域可看作是均质材料,其声弹性系数可通过材料的Lame常数和Murnaghan常数根据声弹性系数公式得出。

(2)结合区域。在加工过程中并非只有涂层材料熔化,基体材料也会熔化,这也导致了涂层和基体之间存在不均匀熔合区域,且熔合线低于原始的基体表面[16-17]。由试件的截面组织图可以看出,该结合区域处于涂层区域和基体区域之间的过渡区域,且其厚度一般较小,约为0.18～0.22 mm。在该结合区域内存在的是非均质材料,其材料性质与涂层材料和基体材料均有所不同,结合功能梯度材料相关研究[18],可近似将基体、涂层与结合区域的材料看成不同的材料分布在各层中,即沿基体到涂层之间过渡的结合区域,基体材料成分渐渐变少,涂层材料成分渐渐变多,如图2所示。

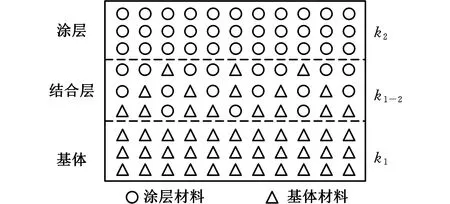
图2 结合区域材料分布模型Fig.2 Material distribution model of combined area

由于涂层材料和制造工艺技术的不同,结合区域形成过程及其对应成分材料往往是不均匀的,从而导致局部区域的材料性质也是不同的[19]。结合区域的材料成分是沿着厚度方向连续变化的,因此材料属性也随着厚度方向连续变化,那么可以对结合区域材料属性提出假设,即由各成分材料属性和分布函数对结合区域材料属性进行建模。

2 结合区域的应力反演方法

2.1 结合区域的声弹性特征

SAYYAD等[20]提出采用成分属性的体积加权平均值近似描述功能梯度材料部分属性;洪轲[21]和张小明[22]等结合功能梯度材料的分布状态和属性研究了超声波传播过程。结合上述研究,为描述结合区域的材料属性,本文提出基于结合区域材料分布状态的材料属性模型,并基于材料属性模型提出结合区域材料分布函数y(r)和结合区域材料声速分布函数z(r)假设,由此建立结合区域声弹性系数模型和声速模型。其中,结合区域材料属性模型为

F=f2+(f1-f2)g(r)

(4)

式中,f1表示基体材料属性;f2表示涂层材料属性;g(r)表示材料属性分布函数;r表示基体材料在结合区域中的体积占比。

结合区域材料的声弹性系数为

k1-2=k2+(k1-k2)y(r)

(5)

式中,k1为基体材料的声弹性系数;k2为涂层材料的声弹性系数。

结合区域材料的声速为

v1-2=v2+(v1-v2)z(r)

(6)

式中,v1为基体材料的声速;v2为涂层材料的声速。

由于结合区域是两种材料的混合区域,结合区域的材料属性介于两种材料之间,所以结合区域的声速是随着结合区域材料的分布状态而变化的,取z(r)=y(r)进行验证。

2.2 涂层结构中声弹性特征表达

按照上述思路可以将单涂层结构推广到多涂层结构,根据各个涂层与基体材料的声弹性特征和分布函数构建结合区域材料属性的一般表达式:

ki-i+1=ki+1+(ki-ki+1)y(ri)

(7)

式中,ki、ki+1分别为相邻两层材料的声弹性系数;ki-i+1为第i层和第i+1层之间的结合区域的声弹性系数;ri为第i层材料在结合区域中的体积占比。

结合区域材料的声速为

vi-i+1=vi+1+(vi-vi+1)z(ri)

(8)

式中,vi、vi+1分别为相邻两层材料的声速。

在多层涂层结构中,会形成多层涂层和多种结合区域,通常这种结构具有1层基体材料和n层涂层材料。涂层结构的材料性质沿着厚度方向发生变化。为方便描述涂层结构的材料性质,以材料表面为零点,沿厚度方向建立轴坐标系,用k(x)表示沿厚度方向的材料声弹性系数函数,用v(x)表示沿厚度方向的材料声速函数。由于涂层结构是分层结构,所以k(x)、v(x)并不是连续函数,而是分段函数,具体表示如下:

(9)

(10)

对于均匀分布的简单一维应力的涂层结构,当超声竖直进入到该涂层结构中时,θ=0°。考虑到结合区域的影响,由式(3)可知,超声波在固定声程中传播的总时间t为

(11)

式中,S0i为各分层材料的厚度;S0i-i+1为各结合区域材料的厚度;v0i为超声波在各材料介质零应力下的传播速度;v0i-i+1为超声波在各结合区域介质零应力下的传播速度。

2.3 涂层结构应力反演模型

由式(3)可以看出,在固体弹性介质中,超声纵波传播时间t会随着应力σ的变化而变化,同时能够推导出超声传播时间差值Δt与应力σ之间的关系模型:

(12)

式中,Δt为由于应力的影响造成的声时差;t0为无应力状态下,超声穿过涂层结构的声时值。

将式(12)变形可得

(13)

超声波的声弹性效应是一种弱效应,即超声波对应力变化不敏感。一般而言,应力变化量为100 MPa时,超声波在铝和钢中的传播速度变化量分别约为0.1%和0.01%,所以Δt≪t0,因此式(13)可表示为

(14)

将式(14)推广至涂层结构,由于涂层结构每层的材料性质是不一样的,所以其每层材料的声弹性系数也不一样,因此需要将其看作是一个整体,涂层结构整体的声弹性系数Ki是由多层材料共同决定的,其中

(15)

r1+r2+…+rn=1

所以涂层结构的应力反演模型为

(16)

3 超声应力检测理论模型验证试验

基于声弹性特征表达和材料属性模型推导应力反演模型(式(16)),设定结合区域分布函数yi(r)并计算涂层结构整体声弹性系数Ki,结合拉/压试验所得的声时值,根据上述涂层结构应力反演模型(式(16))可验证结合区域分布状态的准确性。基于涂层结构分布状态的超声-应力反演流程如图3所示。

图3 基于涂层结构分布状态的超声-应力反演流程图Fig.3 Ultrasound-stress inversion flow chart based on the distribution state of coating structure

3.1 超声检测的试验准备

3.1.1试件的制备

本文选用C45E4作为涂层结构的基体材料,Cu粉末作为涂层结构中的涂层材料,材料的主要成分如表1所示。

表1 试件材料的化学成分

参照国家标准GB/T228.1—2010《金属材料拉伸试验第一部分:室温试验方法》设计试件的尺寸,如表2所示。利用PTA-400E4-ST型数控粉末等离子喷焊机制作涂层原始试件时,将涂层厚度制作为4 mm,试验试件的涂层和基材厚度利用线切割机加工方式均匀加工至2 mm,如图4所示。试件加工成形后,经热处理保证其内部处于无应力状态。

表2 试件的尺寸数值

图4 试件的形状尺寸Fig.4 Shape and dimension drawing of test piece

3.1.2试验设备

试验采用的超声应力检测系统主要由静力加载试验台和DOPPLER相控阵超声检测仪两部分组成,静力加载试验台对试件施加梯度载荷,使用超声检测设备获取应力状态下的超声信号,具体的试验装置、试件加载过程如图5、图6所示。

图5 试验装置图Fig.5 Test setup diagram

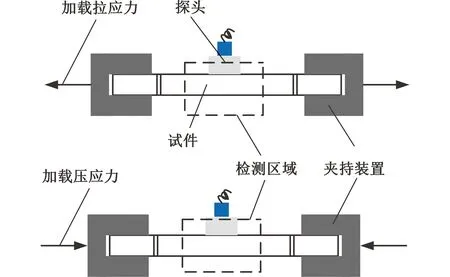
图6 试件加载示意图Fig.6 Specimen loading diagram

为了降低温度对超声传播速度的影响,本试验在恒温环境中进行,相关参数设定如表3所示。在试验过程中,为获取不同应力加载下的超声信号,需要保证拉力或压力保持不变,获取超声信号后再施加载荷。

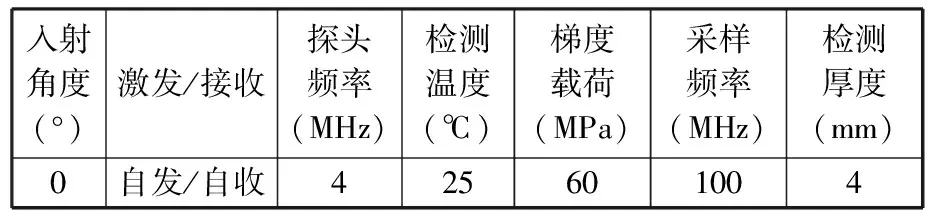
表3 试验参数设定

3.2 试验数据采集及统计

针对单一材料试件和涂层结构试件,按照上述试验参数设定对试件单轴梯度加载的应力(-240～240 MPa),以试件厚度作为声程进行超声检测,获取不同应力状态下的超声传播信号。试验中使用的超声波仪器的采样频率是探头频率的25倍,可以获取超声传播的完整信号,因此可以根据不同的检测范围截取相对应的超声波形图。如图6所示,在试件中心划定一个检测区域,探头位置浮动在该区域中,获取4组超声信号数据,最后将数据进行统计,取试验平均值,形成超声传播时间试验测量平均值表(表4)。

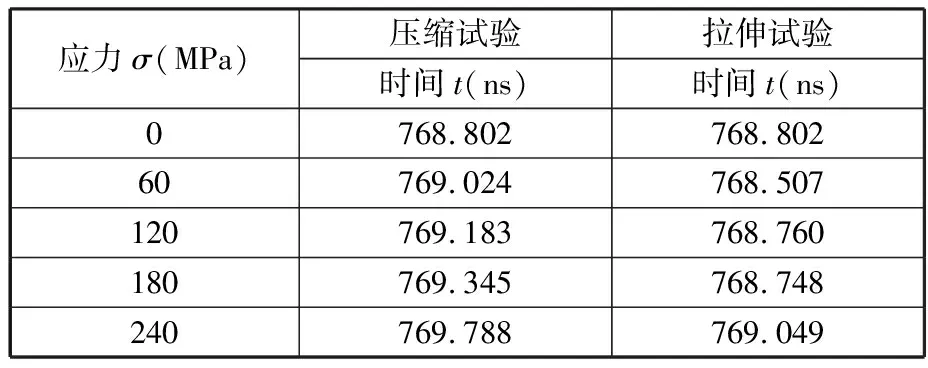
表4 试验测量平均值(Cu涂层)

4 理论验证及分析

由于试件的厚度在应力加载过程中会发生变化,所以该声时变化由两部分组成:应力大小变化对声时的影响和试件厚度变化对声时的影响。因此在对试验数据和反演数据进行对比的过程中,需要考虑试件厚度的变化引起的声时变化。

基于试验所用的试件材料C45E4和Cu粉末,根据声弹性系数表达式、材料属性和弹性常数,可计算得到两种材料的声弹性系数,如表5所示,其中,l、m为固体弹性介质的三阶弹性常数(Murnaghan常数)。

表5 试验试件的材料常数[15]

根据表5给出的基体材料和涂层材料的声弹性系数值和式(5),可计算结合区域的声弹性系数,其相关设定如下:①由于本文是对横截面进行分析,故体积占比可间接采用材料的厚度占比表示。结合功能梯度材料的分布状态[21],预设了3种声弹性特征函数表达(表6)。②由于涂层结构内各区域厚度有波动,结合区域的厚度可通过电镜扫描的方式获得(图1),约为0.18～0.22 mm,所以在计算涂层结构声弹性系数时,取结合区域的平均厚度0.2 mm。③当不考虑结合区域时,涂层与基材厚度可视为2.0 mm,声弹性系数值与函数y1(r)计算值相等,因此,可将基于y1(r)函数的应力反演值等效为未考虑结合区域的应力反演值。④ 在加载应力时涂层结构厚度也会变化,基于形变量公式,每加载60 MPa,Cu涂层区域厚度变化为0.338 μm,C45E4基材区域厚度变化为0.176 μm,仅占涂层结构总厚度的0.064%,会产生声弹性系数变化为0.023%。因此,为简化计算,忽略加载应力时涂层结构厚度变化对涂层结构整体声弹性系数值的影响。

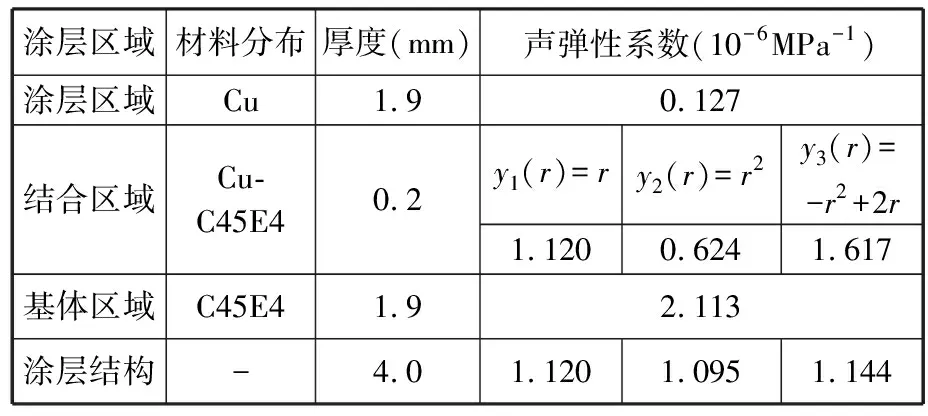
表6 涂层结构材料分布函数下的声弹性系数[21]

基于上述设定,本文提出3种结合区域的材料分布函数,并结合式(15)计算涂层结构整体的声弹性系数Ki,如表6所示。

建立由于应力影响造成的声时差Δt和应力值σ的数值关系,如图7所示。由图7可知,越接近实验值的分布函数误差越小,表明该拟合函数更适于描述喷焊工艺所形成的涂层结合区域材料声弹性特征。

图7 涂层试件声时差的理论值与试验值对比Fig.7 Comparison of theoretical and test acoustic time difference of coating specimen

对表4中试验值进行线性拟合,去除试件厚度变化对声时的影响,计算涂层结构整体声弹性系数为1.043,故引入结合区域分布函数y2(r)的声弹性特征表达的反演值更接近试验值。由式(16)对应力进行反演,可得到涂层结构试件中应力反演值,如表7所示。

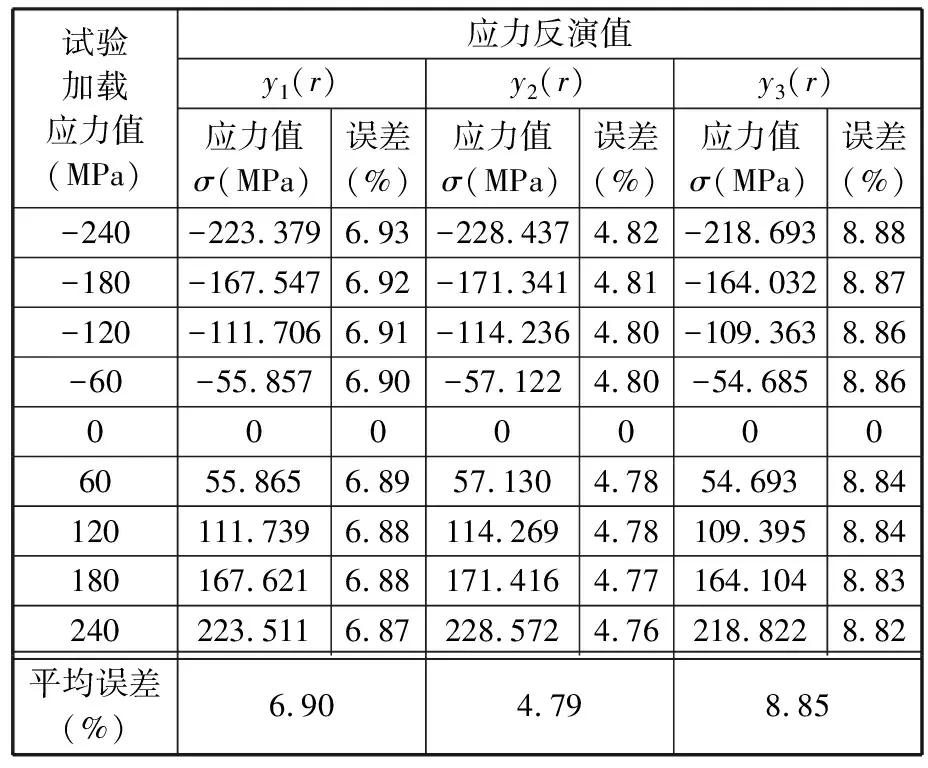
表7 涂层结构试件中应力反演值

由表7可知,基于分布函数y2(r)下的声弹性系数K2所得的反演值比未考虑结合区域的反演值更接近试验值,说明所提出的涂层结构超声传播分析方法的有效性。分布函数y2(r)使结合区域声弹性特征偏向于涂层材料,其潜在原因可能是涂层制备过程中采用了等离子喷焊成形工艺,在熔池形成过程中金属粉末含量较大,影响其结合区域中涂层材料的声弹性特征占比较高。

综上所述,基于材料分布状态提出其对应声弹性特征表达,可以有效修正涂层结合区域材料状态变化所产生的检测误差。由试验数据对比可知,基于分布函数y2(r)下的声弹性系数K2的声弹性特征表达,其反演应力值与实际加载应力值之间平均误差为4.79%,小于未考虑结合区域时的平均误差6.90%。因此,应结合涂层制备工艺,分析其材料-结构成形过程,尤其是结合区域材料分布状态,构建基于材料分布状态的声弹性特征表达,可以有效提高超声应力检测数据的精确性与可靠性。

由于本文中结合区域体积占比仅为涂层结构试件的5%,因此分布函数y2(r)的误差修正效果不够明显,相比于不考虑结合区域检测精度提高2.11个百分点。因此根据上述结论推断可得,在试验中施加60,120,180,240 MPa的应力时,当结合区域体积占比变化时,分布函数y2(r)相比不考虑结合区域的应力反演差值如图8所示。

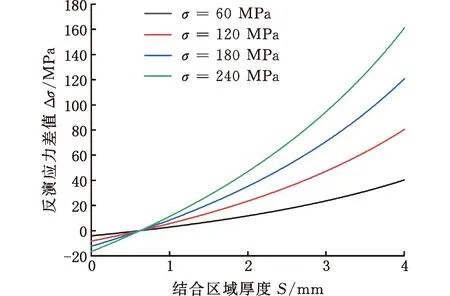
图8 结合区域体积变化时应力反演差值Fig.8 Stress inversion differences when combining regional stress changes

5 结论

本文分析了等离子喷焊增材工艺中涂层结构不同区域材料分布状态及规律,基于声弹性理论,提出金属涂层结构的声弹性特征表达及涂层结构的应力反演模型,并结合涂层-应力超声检测试验予以验证,该模型同样适用于其他方法所制作的涂层结构,本文仅以等离子喷焊增材工艺为例,引出该问题并给予验证。其结论如下:

(1) 涂层结构中材料分布状态,尤其是基材与涂层结合区域内非均质材料分布会直接影响其对应区域的声弹性特征,这种声弹性特征不一致性会导致应力场中超声信号波动及检测误差,因此,需要分析涂层结构材料分布状态。本文提出的基于材料分布状态的声弹性特征表达有助于进一步提高超声应力检测精度。

(2) 结合等离子喷焊工艺制备涂层结构试件,利用应力加载设备开展超声应力检测试验,结果表明:与均一材料分布下声弹性表达相比,基于材料分布状态的声弹性特征表达的应力反演值更接近试验加载值,具备较好修正作用,能有效降低超声应力检测误差。

(3) 针对涂层结合区域中非均质材料分布状态,文中列出了3种拟合表达函数,通过超声应力检测实验对比验证:基于分布函数y2(r)下的声弹性系数K2所得到的应力反演值与试验值平均误差为4.79%,平均误差修正效果较好,表明该拟合函数更适于描述喷焊工艺所形成的涂层结合区域材料声弹性特性。

(4) 在超声应力检测中,通过分析涂层结构中材料不均一分布状态,修正其对应区域的声弹性特征表达,有助于降低涂层结构的应力检测误差。同时,应重点结合不同类型涂层成形工艺、功能梯度材料结构等方面开展其对应声弹性特征表达分析,提高超声应力检测及涂层结构质量评估的精准度与可靠性,支撑超声无损检测技术在增材制造领域的工程化应用。