基于改进离散方法的截割稳定性预测分析

谢 苗 朱 昀 刘 杰 任 泽,4 杨志勇,5 刘治翔王 贺 孟庆爽

1.辽宁工程技术大学机械工程学院,阜新,1230002.辽宁省大型工矿装备重点实验室,阜新,1230003.华能煤炭技术研究有限公司,北京,1000714.国家能源集团国际工程咨询有限公司,北京,1000105.新疆露天矿智能生产与管控重点实验室,昌吉,831100

0 引言

随着煤矿开采技术的发展,人们对煤矿巷道断面成形质量的要求也逐步提高。悬臂式掘进机作为智能化快速掘进的关键设备,对其工作的可靠性和稳定性也有了更高要求。截割机理是研究掘进机设计与制造的关键,一直是智能化截割的研究热点[1-2]。侯祥明[3]对掘进机截割头的受力进行研究,建立了掘进机整机振动方程;李晓豁[4]基于拉格朗日方程建立了整机动力学模型,提出了截割头外载荷虚拟激励法,研究了截割臂振动特性; 魏晓华[5]研究了掘进机摆动过程的非线性静力学、动力学特性,分析了不同工况下掘进机截割性能; ZHANG等[6]对冲击载荷作用下掘进机动力系统力学特性进行了研究;刘治翔等[7]研究了截割头运动轨迹对巷道表面形貌特征的影响,得到了巷道外轮廓的创成机理;袁晓明等[8]通过仿真与实验相结合的方法,研究了截齿截割角和旋转角对截割载荷、载荷波动和截割比能耗的影响规律;WANG等[9]利用线性全尺度截割的原始数据,通过主成分回归分析方法和岭回归分析方法,建立了镐形齿的平均截割力和峰值截割力模型以及考虑镐齿磨损的峰值截割力模型;XU等[10]对截割头截齿安装角度与截割角度的转化关系进行研究,并通过数值仿真的方法研究了截割角度与截割阻力的关系;LIU等[11]对截齿工作角度与截割载荷的关系进行研究,获得了截齿的工作角范围,并通过数值模拟方法进行了截齿工作角度优化;ZHANG等[12]简化了摆动截割中截割头的运动,并通过数值模拟方法研究了截割深度与截割转速对截割性能的影响,获得了最优截割深度区间。

悬臂式掘进机的稳定工作状态是保证它高效可靠运行的重要影响因素,而悬臂式掘进机截割过程中,由于受截割头自身振动的影响,截割厚度会发生改变,从而诱发截割过程中动态截割力变化,引起截割颤振。截割颤振对掘进机的稳定状态有较大影响,但近年来对截割头截割稳定性和截割颤振的研究较少。

目前稳定性预测的方法主要有全离散法、半离散法、数值积分法等。MANN等[13-14]基于时间有限元分析(time finite element analysis,TFEA)理论分析了工件加工过程的稳定性,并对其动态加工误差进行了同步预测;INSPERGER[15]基于半离散法进行加工过程的稳定性预测;DING等[16]提出了基于直接积分框架基础的全离散预测方法;LI等[17-18]利用二阶半离散法同时预测出颤振稳定域和动态加工误差;LI等[19]分析了欧拉公式动力学方程的离散特性,研究了基于完全离散法的工件加工稳定性;LI等[20]对比完全离散法,提出了基于四阶龙格库塔的加工稳定性预测方法。但上述半离散方法的计算精度与计算效率偏低,全离散方法的计算精度虽有所提高,但由于状态空间方程复杂,全离散法对解决现有问题的时间成本依旧很高。

本文在截齿破岩截割机理的基础上,建立了单一截齿截割过程受力模型,推导了截割深度与参与截割截齿数量的关系,进而构建了单个截齿截割状态下的力学特性方程,并基于煤矿截割和金属切削领域的相似性,将金属切削中的刀具颤振模型引入煤矿截割领域进行截割头稳定性分析,提出一种基于牛顿-拉格朗日混合插值的改进全离散方法。为验证所提出方法的有效性,搭建了截割头-煤岩系统试验台,进行了截割稳定性实验验证,结果表明本文提出的牛顿多项式预测方法收敛速度快、预测精度高、计算耗时少,可有效提高截割头截割可靠性,提高截割后煤岩表面平整性,能够为高效弱颤振截割参数的选择提供设计依据。

1 截割头-煤岩系统动力学方程构建

1.1 截齿载荷分析

截齿在楔入煤岩时,受到截割速度前方煤岩的阻力,该力由截割动作产生,称为截割阻力FC;截齿截割时向下挤压煤岩,受到煤岩的反力,该力垂直于截割速度方向,由截割部的进给动作产生,称为进给阻力FN;截齿截割成槽时,两侧煤岩脆性崩落,同时,截齿受到截槽两侧的反力,该力垂直于齿尖两侧分布,称为侧向阻力FS。处于截割状态的截齿受力情况如图1所示。

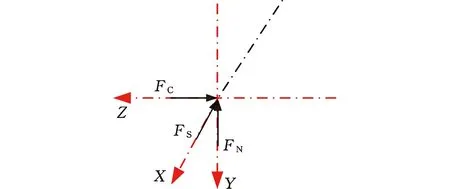
图1 单个截齿受力Fig.1 Force on single pick

通过截割头载荷计算经验公式可得悬臂式掘进机在井下煤巷工作时作用在截割头上的截割阻力[21]

FC=K1+K2h

(1)

K1=0.25pkKtKsKa+0.1pkST

和锥形截齿受到的阻力

FN=K3FC/h0.4

(2)

K3=2.5(0.15+0.000 56pk)

以及侧向阻力

(3)

其中,h为瞬时截割厚度;pk为岩石接触强度,与截割岩石硬度有关;f为岩石普氏硬度系数;Kt为截齿的类型系数,锥形齿为1.5,刀型齿为1;Ks为与截齿形状相关的系数;Kts为刀头形状系数;K′ts为刀杆分布形式系数;Ktd为刀头直径系数;Kb为刀型齿齿间刀刃宽度影响系数,与刀刃宽度b线性相关,Kb=0.92+0.01b;Kas为刀型齿齿面前刃面形状影响系数,平面取1,椭圆形或尖形取0.95;Ka为截齿截割角影响系数;β为平均截线间距,mm;ST为截齿后刃面磨钝后在牵引方向的投影面积,mm2;C1、C2、C3为截齿布置系数,顺序式时C1=1.4,C2=0.3,C3=0.15,交叉式时C1=1.0,C2=0.2,C3=0.1。

截割载荷主要受岩石性质参数、截齿结构和形状以及截割头结构以及截割头工作参数影响,对于井下工作的悬臂式掘进机,其截齿形状和截割头的整体结构都基本固定,对于同一区域的煤层,煤层性质参数可视为相对固定,因此,截割载荷仅与截割厚度h与截割头工作转速n、截割头钻进速度vs有关。

1.2 截割头载荷分析

图2 截割头载荷Fig.2 Cutting head load

截割头上第i个截齿三向分力分别为

(4)

式中,φi为截齿所在的位置角,(°)。

由于截割头整体载荷大小与参与截割的截齿数紧密相关,截割齿数又因截割头钻进深度、截割头工作状态的不同而发生改变,因此通过对截割头形貌的实际测量能够获得截割深度和参与截割截齿数量的关系。假设截割头深度为hd,截割头参与截割的工作齿数为z,以国产EBZ160型悬臂式掘进机为例,其截割头长度为975 mm,根据截割头截齿位置设计参数得到截割头截割深度与参与截割的齿数关系如表1所示。

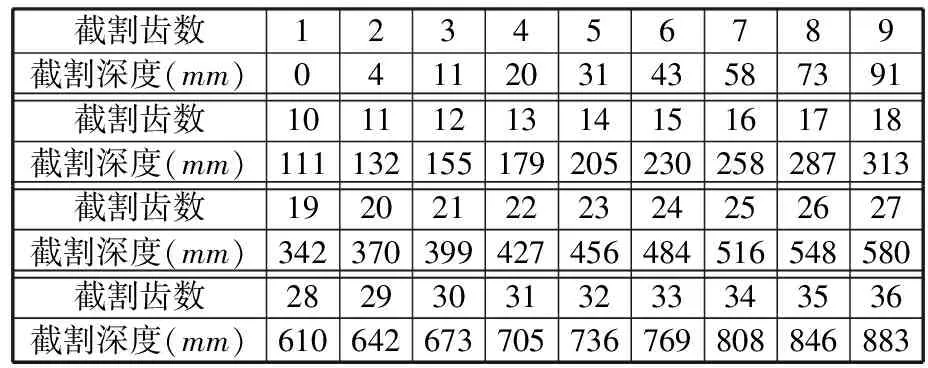
表1 截割深度与截割齿数关系

采用最小二乘法拟合的方式对截割深度与截割头工作齿数进行拟合,可得到在水平摆动或者垂直摆动工况下,工作区截割齿数与截割头截割深度的函数关系式。由于截割头齿数必须为整数,而函数拟合结果可能为小数,故对z=f(hd)向下取整:

(5)

通过最小二乘法拟合的截割深度与截割齿数关系与测量数据的对比如图3所示,图中柱状图为拟合值与测量值的误差绝对值,从中能够看出拟合数据与测量数据存在一定误差,但整体偏差不大。通过R2方法对拟合效果进行评估,计算所得R2=0.995,说明整体拟合效果较好,能满足使用要求。

图3 截割深度与截割齿数拟合曲线Fig.3 Fitted curve of cutting depth and number of cutting teeth

同时,截割头截割齿数还与截割头工作状态有关,通过下式表示:

(6)

其中,N为各工作状态下截割区内的截割齿数,如图4所示。

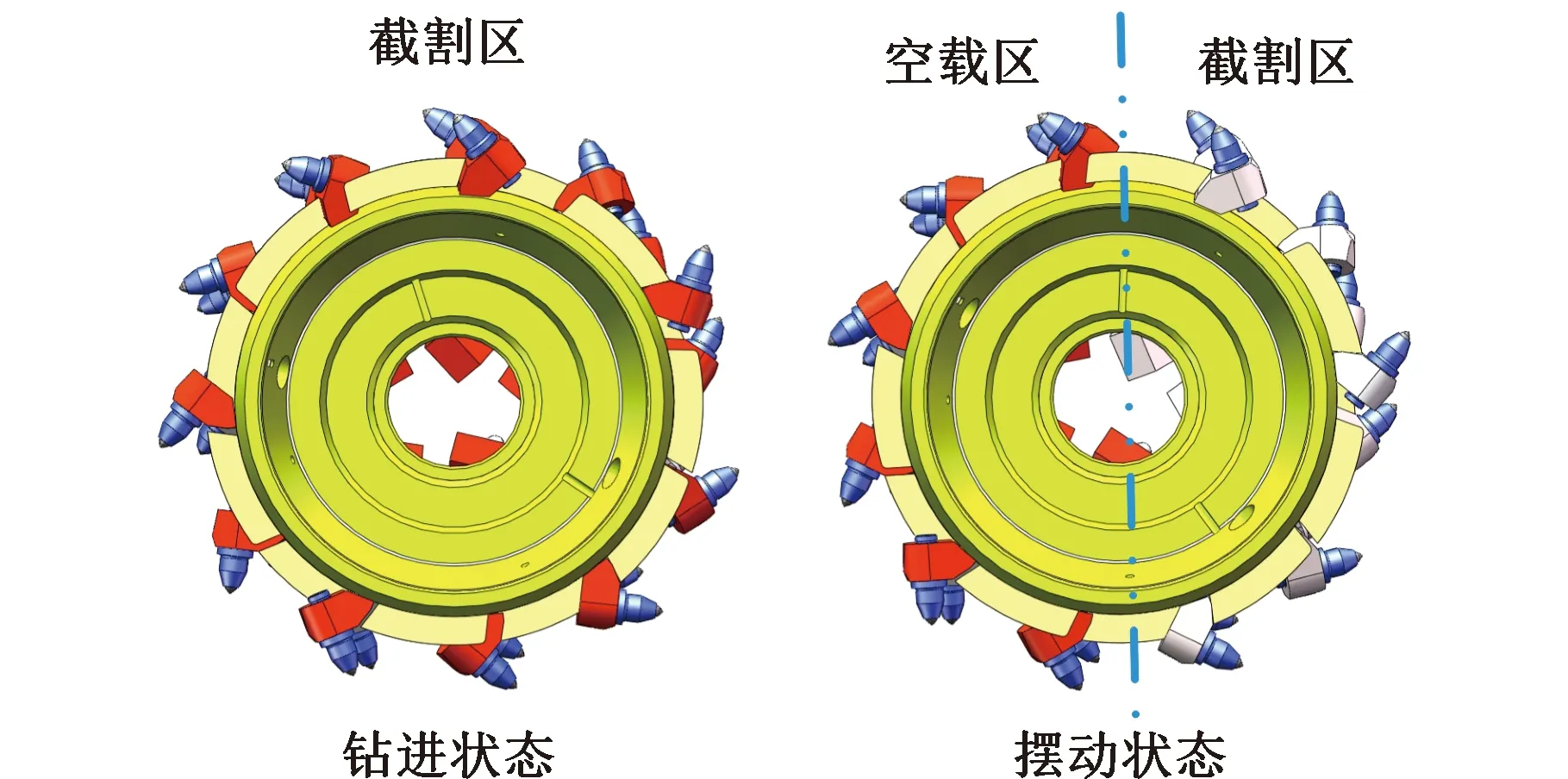
图4 截割头各工作状态截割齿数Fig.4 Number of cutting teeth for each working state of cutting head

基于力线平移理论,对同一时刻位于截割区内的截齿受力进行矢量求和,得到截割头垂直方向、水平方向、轴向方向上的三向力,其中,截割头沿摆动方向横切阻力为

(7)

截割头垂直方向载荷为

(8)

截割头钻进阻力为

(9)

1.3 截割头动力学方程构建

假设悬臂式掘进机的截割头振动幅值在弹性变形范围内,则可根据叠加原理,将截割头的振动视为Fx、Fy、Fz三方向轴向力单独作用的叠加。由此,将截割头简化为三自由度系统,建立煤岩截割过程的截割头系统动力学模型,如图5所示。

图5 截割头系统动力学模型Fig.5 Dynamic model of cutting head system

截割头截割运动的动力学方程表示为

(10)

F(h,t)=[F1F2F3]T

(11)

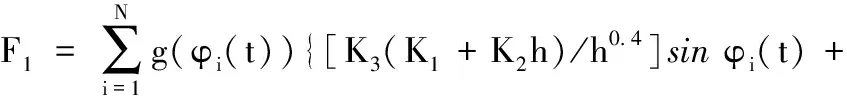
式中,M、C、K分别为截割头的模态质量矩阵、阻尼矩阵和刚度矩阵;mx、my、mz、ζx、ζy、ζz、ωnx、ωny、ωnz分别为x、y、z方向的模态质量、阻尼比和固有频率;s(t)为当前时刻刀具振动位移;F(h,t)为截割头受到的截割载荷,与截割厚度与时间有关。

截齿角速度φi(t)表达式为

φi(t)=(2πn/60)t+(i-1)2π/z

(12)

判断截齿是否参与截割的函数为

(13)

式中,ωin为第i个截齿开始截割位置;ωout为第i个截齿结束截割位置。

对于逆时针截割,ωin=0,ωout=arccos(1-ae/R);对于顺时针截割,ωin=arccos(1-ae/R),ωout=π。其中,ae为径向切深,R为截割头半径。

动态截割厚度hi(t)表示为

hi(t)=h0+(si(t-T)-si(t))

(14)

式中,h0为理论截割厚度;si(t)、si(t-T)分别为当前t时刻的截齿动态位移和超前一个周期对应时刻(t-T)时的截齿动态位移,如图6所示。

图6 动态截割厚度变化Fig.6 Dynamic cutting thickness change

由于截割厚度的变化仅体现在截割头截割的X、Y方向,因此动态截割厚度Δh可以通过截齿动态位移表示:

Δh=-Δxsinφi(t)-Δycosφi(t)

(15)

对式(11)中含hi(t)项进行泰勒展开:

(16)

由于动态位移相对较小,可以忽略不计,故舍去展开式中高次项。

将式(14)～式(16)代入式(11)中,并将其表示成矩阵形式为

(17)

式中,αxx、αxy、αyx、αyy、αzx、αzy分别为随时间变化的方向系数。

令

那么在结构动力学框架下,截割头动力学方程可以表示为以下时滞微分方程:

(18)

考虑到截割力模型是线性的,故计算截割头再生颤振稳定性时可忽略与动态位移无关的静态量,得到

(19)

2 截割头-煤岩系统截割稳定性预测

2.1 基于牛顿-拉格朗日混合插值方法的截割稳定性预测

令

(20)

将式(19)的动力学方程表示为状态空间形式进行求解,得

(21)

将周期T划分为m份(T=mτ),并利用直接积分法对状态空间表达式进行求解,获得式(21)的响应:

γ(t)=exp(A0(t-kτ))γ(kτ)+

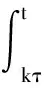
(22)

当时间t=(k+1)τ时,对应的响应γk+1为

(23)

分别采用牛顿插值与拉格朗日插值对式(23)中的积分项进行近似计算,对式中A(kτ+τ-δ)与B(kτ+τ-δ)项采用一阶拉格朗日方法依据(kτ,(k+1)τ)区间端点值进行插值,对式中的γ(kτ+τ-δ)项,采用三阶牛顿插值多项式进行近似计算,对式中的延时项γ(kτ+τ-δ-T)采用拉格朗日多项式进行插值,通过上述插值,式(23)能够表示为

(I-Fk1)γk+1=(F0+Fk)γk+Fkp1γk-1+
Fkp2γk-2+Fk1mγk+1-m+Fkmγk-m

(24)

(25)

因此,γk+1可以通过前一时刻的状态响应表示,其矩阵形式为

(26)

C11=(I-Fk1)-1(F0+Fk)
Cp1=(I-Fk1)-1Fkp1
Cp2=(I-Fk1)-1Fkp2C1m=(I-Fk1)-1Fk1m
Cm=(I-Fk1)-1Fkm

截割头状态空间表达式对应的状态转移矩阵Φ可以通过映射函数Dk表示,即

(27)

依据Floquet理论,根据状态转移矩阵特征值的模对系统稳定性进行判定:

(28)

2.2 稳定性验证与分析

设定截割系统X、Y、Z方向模态参数相同,截割部摆动速度vt=0.5 m/s,截割头转速n=45 r/min,截割的煤岩状态为煤岩夹杂,煤岩硬度为4,岩石接触强度pk为350 MPa[22],设置截割头截割深度分别为200 mm、400 mm和800 mm。

对比改进混合离散法、全离散法和半离散法对本文方法进行验证,通过局部离散误差‖U|-|U0‖对离散方法的收敛速度进行验证[23],其中,|U|表示状态转移矩阵特征值的模,|U0|为m=200时采用二阶全离散方法得到的精确值。

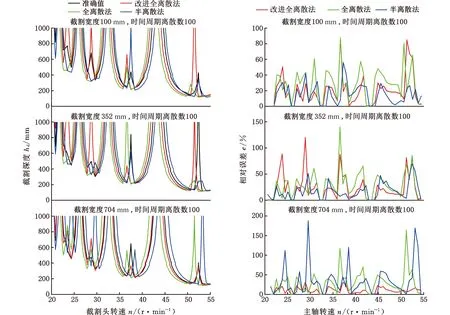
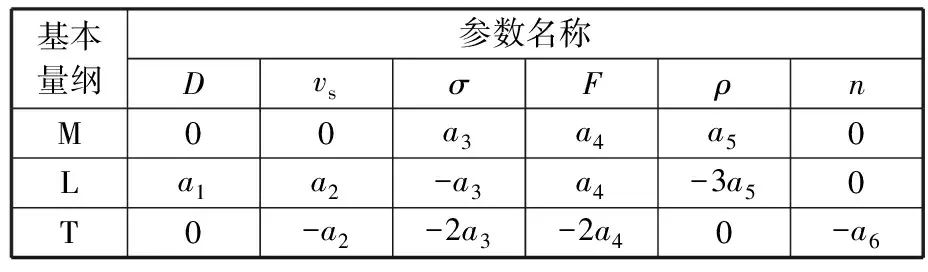
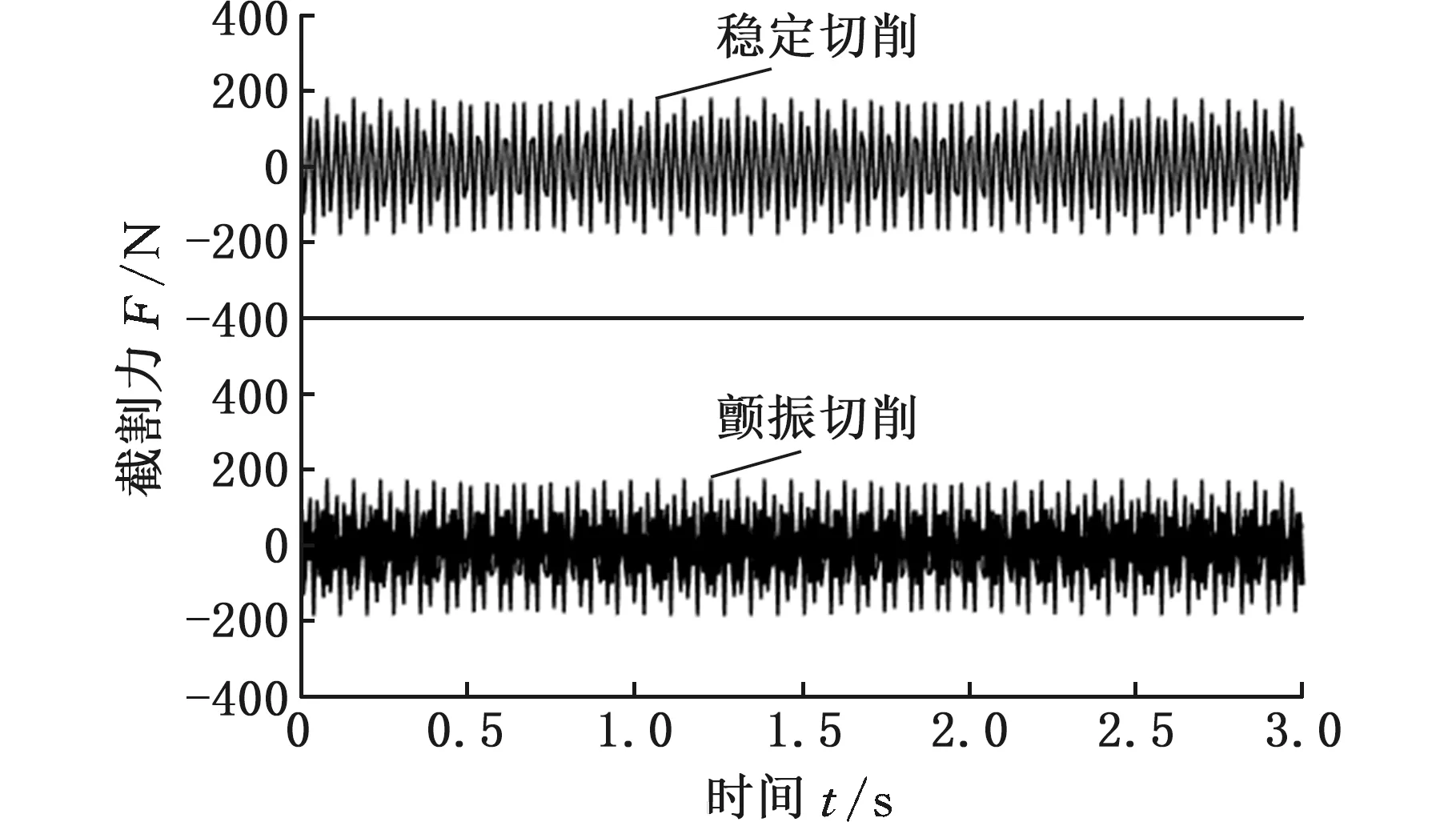
首先对改进全离散方法的收敛速度进行对比,计算得到收敛速度曲线如图7所示。当转速在20 r/min

(a)截割深度为200 mm收敛状态

(a)截割深度 (b)相对误差图8 不同预测方法预测精度对比Fig.8 Comparison of prediction accuracy between different prediction methods

(a)截割宽度100 mm

由图7可以看出,改进全离散方法的初始离散误差明显小于其他方法,随着时间周期离散数m的增大,改进全离散方法的收敛速度也在一定程度上优于全离散法和半离散法。

为了客观评估各方法间的收敛速度、预测精度,选用均方根误差(root mean square error, RMSE)作为评价指标进行度量,计算公式如下:

(29)

由式(29)计算三种深度下各方法的σRMSE并取平均值,最后得到采用全离散法的均方根误差为0.0945,半离散法的均方根误差为0.0445,而采用改进后的离散方法计算所得的均方根误差仅有半离散法的一半,为0.0275,这表明采用改进后的离散方法计算获得的特征值的模在相同离散数下更加接近真实值,客观地说明了本文方法在收敛速度上相较其他方法更快。

图8a为不同方法计算获得的截割深度叶瓣图对比,而图8b所示为不同方法获得的截割深度预测值与准确值之间的相对误差。由图8可以明显看出,随着切割宽度的变化,每种离散方法的预测结果都有一定的偏差。但对比不同方法的相对误差可以清楚地看到,改进的离散方法相较于其他两种方法的相对误差曲线处于较低的水平,表明在计算精度上具有一定的优势。

同样地,采用均方根误差为评价指标对不同方法间的误差水平进行度量,计算不同截割宽度下的均方根误差并取平均值,最后得到的均方根误差如表2所示。可以看出,通过改进离散方法计算获得的截割深度均方根误差相较于全离散方法获得的截割深度均方根误差减小了8.9%,表明通过改进离散方法获得的叶瓣图曲线更为准确,预测精度更高。

表2 不同方法均方根误差比较

不同方法不同截割宽度下的计算时间对比如图9所示,可以看出,随着时间周期离散数的增大计算耗时明显增加,而随着截割宽度的变化,计算耗时的变化不明显。同时对比不同计算方法间的计算时间可以得出,采用半离散与改进全离散方法的计算耗时较为接近,均较全离散方法节省约1/3的计算时间。

从上述分析中能够看出,随着截割宽度的变化,各离散方法预测结果均有一定偏差,预测效率也各有优劣,但在计算参数相同条件下,本文提出的改进全离散方法预测精度更高,预测效率更高、预测的稳定截割边界更为准确。分析结果表明,相较其他离散方法,改进全离散法在几乎不损失计算精度的情况下提高了截割头-煤岩系统的颤振分析预测效率。

3 截割颤振影响因素分析

由上述分析建立的截割头-煤岩系统动力学模型可知,截割系统的动力学参数对系统稳定性的预测有一定影响,过大的系统刚度与较大的系统阻尼会降低截割头振动幅度,加载到煤岩表面会减缓系统颤振,提高系统稳定性,影响断面成形质量。因此,本文通过改变截割系统模态刚度、固有频率和阻尼比,研究不同的参数组合对截割-煤岩系统稳定性的影响。

3.1 系统模态刚度对颤振稳定性的影响

为了分析系统模态刚度K对系统颤振稳定性的影响,通过改变模态质量对系统模态刚度进行调整,计算得到的稳定性叶瓣图见图10。由图10可知,截割深度与截割转速间的叶瓣图趋势随着刚度的增大逐步上移,截割稳定性区域面积随刚度的增大持续扩大,系统稳定性逐步增强。

图10 不同模态刚度下截割系统稳定性曲线Fig.10 Stability curve of cutting system with different modal stiffness

3.2 系统阻尼比对颤振稳定性的影响

对阻尼比与截割稳定性影响关系进行研究,计算得到稳定性叶瓣图见图11。从图中可以看出,与系统模态刚度影响趋势近似相同,随着阻尼比的增大截割稳定性叶瓣图向上移动,系统稳定性区域逐步扩大,意味着可以通过提高系统阻尼比对系统颤振稳定性进行改善。

图11 不同阻尼比下截割系统稳定性曲线Fig.11 Stability curve of cutting system with different damping ratio

3.3 系统固有频率对颤振稳定性的影响

为分析固有频率对截割稳定性的影响,选用的固有频率值为209,229,249,269 Hz,计算得到的稳定性叶瓣图见图12。由图12可知,当固有频率增大时,叶瓣图向左移动,同时由于固有频率对系统刚度和阻尼的影响,增大固有频率还会使叶瓣图逐步上移,提高相同转速下的极限截割深度。

图12 不同固有频率下截割系统稳定性曲线Fig.12 Stability curve of cutting system with different natural frequencies

4 截割头-煤岩系统稳定性实验验证

4.1 实验样机的相似准则推导

本文提出的颤振预测模型通过搭载截割头-煤岩试验台进行验证。依据相似实验准则分别建立截割头实验模拟样机、实验模拟煤壁。

在进行截割头实验模拟样机设计时,以截割头主要参数(包括截割头几何参数与运动参数)与煤岩性质参数进行相似准则推导。

其中,截割头结构参数以长度L的量纲为基本量纲,在进行相似准则推导时可以进行适当简化,仅选取一个参数进行推导,本文选用截割头外径D进行参数推导,具体参数量纲表如表3所示。

表3 截割头结构参数

而截割头上决定截齿整体布置方法的截齿齿间夹角α、叶片沿螺旋线升角αu、截割头上方截齿的类型及形状、单截线上截齿数量np都是与基本量纲无关的量纲一参数,在相似准则推导时可以看成独立π项,不参与计算。

截割头的运动参数则包括截割头钻进速度vs、截割头转速n、截割头截割力F。煤岩性质参数主要包括煤岩密度ρ和抗压强度σ,具体参数量纲表如表4所示。

表4 截齿头运动参数与煤岩性质参数及其量纲

从上述分析可知,本相似实验模型需要考虑推导的相似准则参数共有6个,分别为截割头外径D、截割头钻进速度vs、截割头转速n、截割头截割力F、煤岩密度ρ和抗压强度σ。而由量纲分析可知,截割头外径D、钻进速度vs以及抗压强度σ能够对应掘进机EBZ160的结构、运动以及煤岩性能参数,同时包含了三个基本量纲,因此可以选择以上三个参数作为基本物理量参数,获得所有6个参数的量纲矩阵,如表5所示。

表5 相似实验样机关键参数的量纲矩阵

基于上述量纲矩阵,进行相似准则推导,获得如下方程组:

(30)

通过上述分析计算得到所选择三个物理量相关的π矩阵如表6所示。

表6 相似实验样机相关参数的π矩阵

由上述推导获得的π矩阵可以得到各相似准则参数对应的指数:

(31)

假设掘进机EBZ160的原物理量参数为x,相似实验模型的模型物理量参数为xm,那么各参数相似系数可以表示为Cx=xm/x,根据相似第一准则,可以获得各相关参数之间的计算表达式如下:

(32)

在建立试验台相似模型时,为了方便整体换算,以长度L为基准量,设其相似系数为Cl=1/Ks,Ks为设定的相似比例常数。

设定煤岩特性参数的相似性,设定煤岩密度参数的相似系数表示为Cρ=Cσ=1,由此推导出所有相似系数如下:

(33)

考虑到实验室现有条件限制与截割实验相似系数选取经验[24],按照1∶3的相似比建立EBZ160掘进机的相似实验模型,即取Ks=3,得到相似实验台与实际工况的参数对比如表7所示。

表7 相似实验台与实际工况参数对比

保证截割的几何参数保持相对一致、实验截割头的转速满足实际掘进机截割转速范围(69～138 r/min),同时为了保证相似实验模型的准确建立,将截割头电机后置,如图13所示。

图13 截割头-煤岩系统试验台Fig.13 Cutting head-coal rock system test bed

同样,根据相似实验理论建立煤壁的相似实验模型,选用煤粉、水泥、水进行配比,取天然煤岩的抗压强度为80 MPa[25],考虑到天然煤壁的自身裂隙与节理特征,最终确定实验煤岩的抗压强度为32 MPa。通过改变煤壁模型的原材料制备不同比例下的煤样试件,如图14所示。

(a)试件一 (b)试件二 (c)试件三 (d)试件四图14 煤岩试件Fig.14 Test coal rock sample

最终通过济南天辰DW-100A型电子式万能实验机进行单轴抗压实验,确定相似实验煤壁采用的最终材料配比为1.62∶1∶0.49。

4.2 截割稳定性实验验证

为了验证改进混合离散预测方法在截割颤振中的正确性,进行截割头-煤岩系统模态参数辨识实验,测试过程如图13所示,截割系统测点布置如图15所示。表8列出了力锤模态试验获得的截割头模态参数。

表8 截割系统模态参数

图15 截割系统测点布置Fig.15 Cutting system measuring point layout

为了验证颤振稳定域曲线的正确性,进行稳定截割和颤振截割两种工况下截割力实验,得到截割力随时间变化的曲线及截割频域曲线如图16所示。分析实验结果可知,截割颤振发生时,截割力倍频增大,颤振信号多集中于截割力倍频附近,影响截割头的稳定性。

(a)截割力时域信号

基于仿真实验得到的截割头模态系数及固有频率,建立颤振稳定域曲线。为了验证截割稳定性叶瓣图的正确性,选用一系列截割深度与主轴转速的组合进行实验验证,结果如图17所示。可以看出,实验结果基本符合稳定性预测状态,表明建立的混合离散模型能够很好地适应截割稳定性预测。

图17 截割稳定性叶瓣图曲线Fig.17 Cutting stability lobe diagram curve

5 结论

(1)基于悬臂式掘进机截割头煤岩多重交互作用机理,建立了单个截齿截割载荷模型,并基于实体三维模型,拟合了截割头截深与参与截割截齿的函数表达,基于截割头载荷与截齿载荷的映射关系,构建了截割头动态截割状态力学特性方程。

(2)基于Floquet理论,选用基于牛顿-拉格朗日混合插值的改进离散方法对截割动力学方程中的动态颤振力的非齐次项进行离散求解,构建了表示截割颤振临界稳定性的叶瓣图曲线并与常用离散方法进行了对比验证。结果表明,所提出的改进离散方法在收敛速率、预测精度和预测效率方面均优于全离散法和半离散法。

(3)基于改进离散方法研究了系统模态质量、刚度和阻尼比对截割系统稳定性的影响,结果表明,当其他系统参数一定时,提高系统模态刚度、阻尼比与固有频率均能有效提高截割系统颤振稳定性,为高效弱颤振截割参数的选择提供了一种有效方法。

(4)搭建截割头-煤岩试验台进行截割头-煤岩系统截割稳定性实验。实验结果表明,采用截割头-煤岩多重交互效应与速度效应的动力学模型以及改进混合离散方法获得的稳定性叶瓣图能够很好地贴近实际截割状态,验证了所建立的改进离散方法与动力学模型的有效性。