大跨距复合材料结构弯曲载荷监测及定位方法

闫东东 胡宇博 郎利辉 秦成伟 张三敏 李 勇

1.北京航空航天大学机械工程及自动化学院,北京,1001912.中车唐山机车车辆有限公司,唐山,064000

0 引言

碳纤维复合材料因其比强度高、比刚度大、耐疲劳和可设计性强等优点广泛应用于航空航天、轨道交通和汽车工业等领域[1-2],例如高铁转向架[3]、航空飞行器的机身和中央翼盒[4]等关键结构。复合材料部件在工作过程中受到过大载荷时会在材料内部出现局部损伤[5],对复合材料的安全性和可靠性产生严重影响,因此实时监测复合材料关键承载部件载荷状态,掌握复合材料部件工作过程中关键载荷数据,能够为操作人员提供准确的复合材料构件工作状态,这对保障复合材料构件安全工作、减少构件检修次数具有重要意义。

弯曲载荷是复合材料构件服役过程中常见的载荷形式[16-17],ULLAH等[18]采用试验和数值模拟相结合的方法研究了复合材料在大挠度弯曲载荷作用下的力学行为,通过建立有限元模型对弯曲载荷下的响应进行了预测;ROHDE等[19]采用数字图像相关技术研究了复合材料梁在弯曲载荷作用时产生的弯扭耦合响应,表征了复合材料梁的弯扭耦合程度;WYSMULSKI等[20]以碳纤维复合材料短柱为研究对象开展了轴心和偏心压缩试验,研究了偏心载荷对碳纤维复合材料短柱临界载荷的影响规律;KIM等[21]采用玻璃纤维增强复合材料研制了一种新型地铁转向架框架,在140 kN载荷作用下进行抗弯性能测试,研究发现侧梁的高度变化对弯曲挠度的影响最大;KIM等[22]通过优化转向架悬吊连接部位的螺栓位置对复合转向架框架在三种主要服役载荷下的结构完整性进行了评估;JEON等[23]对复合材料轻型转向架框架的疲劳寿命和强度进行了评价。以上研究主要集中在弯曲载荷作用下复合材料的响应特性,对具有跨距大、载荷集中等特点的关键承载部件所受弯曲载荷大小和载荷位置的监测研究较少,缺少工程应用时对复合材料大跨距弯曲载荷状态的监测研究。

本文结合高铁转向架以及重载货车板簧等关键承载部件跨距大、载荷集中的工况特点,对大跨距复合材料弯曲载荷大小及位置的监测进行了研究。主要分为复合材料中心加载和偏心20 mm加载两种载荷形式,通过在复合材料表面粘贴FBG传感器的方式开展复合材料弯曲载荷大小监测及定位研究。首先通过理论计算获取碳纤维复合材料弯曲载荷作用下对应位置的应变,验证了有限元模型的有效性;然后采用弯曲载荷试验测试的方法,测量了复合材料弯曲载荷作用下FBG传感器对应位置的应变值,建立了复合材料弯曲载荷大小和加载位置的求解模型,通过对比模型计算结果与实际载荷大小和位置,验证了基于FBG传感器的复合材料弯曲载荷监测和定位方法的有效性。

1 材料与方法

1.1 测试方法及试验材料

高铁转向架复合材料侧梁板具有跨距大、载荷集中的工况特点,如图1a所示,转向架侧梁板主要受到弯曲载荷作用,跨距和总长度比约为0.85。针对侧梁板尺寸大、制造和性能测试成本高、需要专用测试装备等限制,为实现实验室环境的弯曲载荷大小和载荷位置监测,设计了图1b、图1c所示的弯曲性能测试试验。在保证构件跨距和总长度比为0.85大跨距特点的同时,简化了复合材料结构,缩小了复合材料尺寸,碳纤维复合材料测试样件的尺寸为400 mm×40 mm×5 mm,弯曲测试跨距为340 mm。其中图1b所示为压头加载位置处于碳纤维复合材料中心,图1c所示为压头加载位置处于碳纤维复合材料中心右侧20 mm处。对复合材料弹性变形范围内的应变进行监测,载荷的大小对监测的精度影响较小,因此选取表1所示的弯曲载荷作为试验载荷,每种载荷施加5次,传感器S1和S2采集每种载荷的5次反射波长信息。

表1 弯曲载荷加载情况

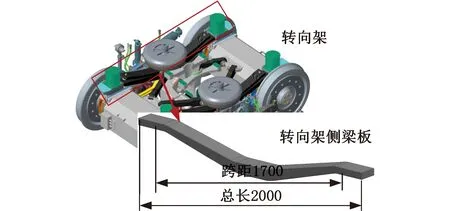
(a)转向架及侧梁板三维结构示意图

试验用纤维材料为上海晋飞技术股份有限公司生产的ST001/T700碳纤维预浸料,碳纤维预浸料单层厚度为0.192 mm。将40层碳纤维预浸料按照[0°/45°/-45°/90°]s的铺层方式铺放,采用热压罐固化工艺制备复合材料测试样件,成形压力为0.7 MPa,成形温度为135 ℃。FBG传感器对称粘贴于距离碳纤维复合材料两端60 mm的位置,如图2所示。

图2 表面粘贴FBG传感器的碳纤维复合材料Fig.2 Carbon fiber composites bonded with FBG sensors on the surface

采用中航工业北京长城计量测试技术研究所开发的FBG传感器进行监测,传感器直径为125 μm,光栅长度为10 mm。弯曲试验在CTM 100G万能试验机上进行,如图3所示,弯曲载荷加载速率为1 mm/min;解调仪采用中航工业北京长城计量测试技术研究所开发的GC-97001C-40-08型解调仪,解调仪参数为:8通道,1000 Hz采样频率,中心波长范围为1520～1560 nm,波长稳定性为±5 pm,波长精度为1 pm。在弯曲载荷加载过程中FBG传感器监测到的光信号经解调仪解调并传输至计算机软件保存,结合测量数据计算获得碳纤维复合材料FBG传感器对应位置的应变值。

图3 FBG传感器监测碳纤维复合材料弯曲载荷试验过程Fig.3 FBG sensor monitoring the carbon fiber composite bending load test process

1.2 FBG应变监测原理

FBG传感器在直径为7 μm的纤芯内部刻有光栅,表面被直径为125 μm的涂覆层包裹,光栅可以反射透射光的某一波长(中心反射波长)。FBG传感器中心反射波长的表达式如下:

λB=2neffΛ

(1)

式中,neff为FBG传感器的有效折射率;Λ为FBG传感器的栅格常数。

有效折射率neff和栅格常数Λ的变化与光栅轴向应变εz和温度变化ΔT有关,应变εz通过弹光效应影响有效折射率neff,通过光纤长度变化影响栅格常数Λ;温度变化ΔT通过热光效应影响有效折射率neff,通过热膨胀效应影响栅格常数Λ。FBG传感器的波长变化监测原理如下:

(2)

式中,KT为温度灵敏度系数;ΔλB为波长变化量;Kε为FBG传感器的应变灵敏度系数;KT为FBG传感器的温度灵敏度系数。

1.3 载荷大小及加载位置理论推导

分析碳纤维复合材料受弯曲载荷作用时的基本假设为:①碳纤维复合材料中单层板为均质连续的线弹性体,即不区分纤维和基体材料;②碳纤维复合材料是均质连续的线弹性体,即不区分铺层的微观结构的差别;③单层板或层合板在弯曲载荷的作用下变形较小,即在力学分析时可按结构的原始尺寸进行计算;④碳纤维复合材料弯曲变形时中性轴位置不发生改变,即在力学分析时中性轴为上下表面中间层所在位置。

如图4所示,碳纤维复合材料两端简支受到线载荷作用,FBG传感器粘贴在碳纤维复合材料表面,载荷施加过程中可由FBG传感器监测碳纤维复合材料指定位置的应变ε,复合材料对应位置沿长度方向的应力σ=E1ε,其中E1为碳纤维复合材料纤维方向的弹性模量。FBG传感器S1测得的应变为ε1,FBG传感器S2测得的应变为ε2,由材料力学弯曲载荷计算公式可得到碳纤维复合材料载荷F的大小和位置。

图4 弯曲载荷受力分析示意图Fig.4 Schematic diagram of bending load analysis

传感器S1处的应力σ1可表示为

(3)

式中,M1为传感器S1处的扭矩;y为碳纤维复合材料厚度的1/2;Iz为碳纤维复合材料的转动惯量。

传感器S1处的扭矩M1可表示为

(4)

式中,L为支点A到支点B的长度(跨距);F为所受载荷的大小;x为载荷F的位置到支点A的距离;a为传感器S1到支点A的距离。

碳纤维复合材料的惯性矩Iz可表示为

(5)

式中,w为碳纤维复合材料的宽度。

由于本文试验周期最长不超过5 min,室温温度变化可以忽略不计,因此ΔT=0,Kε=0.784[24]。

传感器S2处的应力σ2可表示为

(6)

传感器S2处的扭矩M2可表示为

(7)

式中,b为传感器S2到B点的距离。

由式(3)～式(7)可以计算得到载荷大小F和加载位置x,F可表示为

(8)

x可表示为

(9)

1.4 复合材料应变计算

如图4所示,对受弯曲载荷作用碳纤维复合材料作出如下假设:①层间变形一致假设,即层合板各单层之间粘接牢固,层间变形一致,无相对位移;②直法线不变假设,即变形前垂直于板中面的直线在板变形后仍保持垂直,且长度不变;③σz=0假设,即在厚度方向上的正应力与其他应力相比很小,可以忽略不计;④单层平面应力状态假设,即层合板中各单层都可以近似地认为处于平面应力状态[25]。

1.4.1单层板刚度特性

如图5所示,纤维方向与材料方向存在夹角θ时,纤维方向应力与材料主方向应力关系可表示为

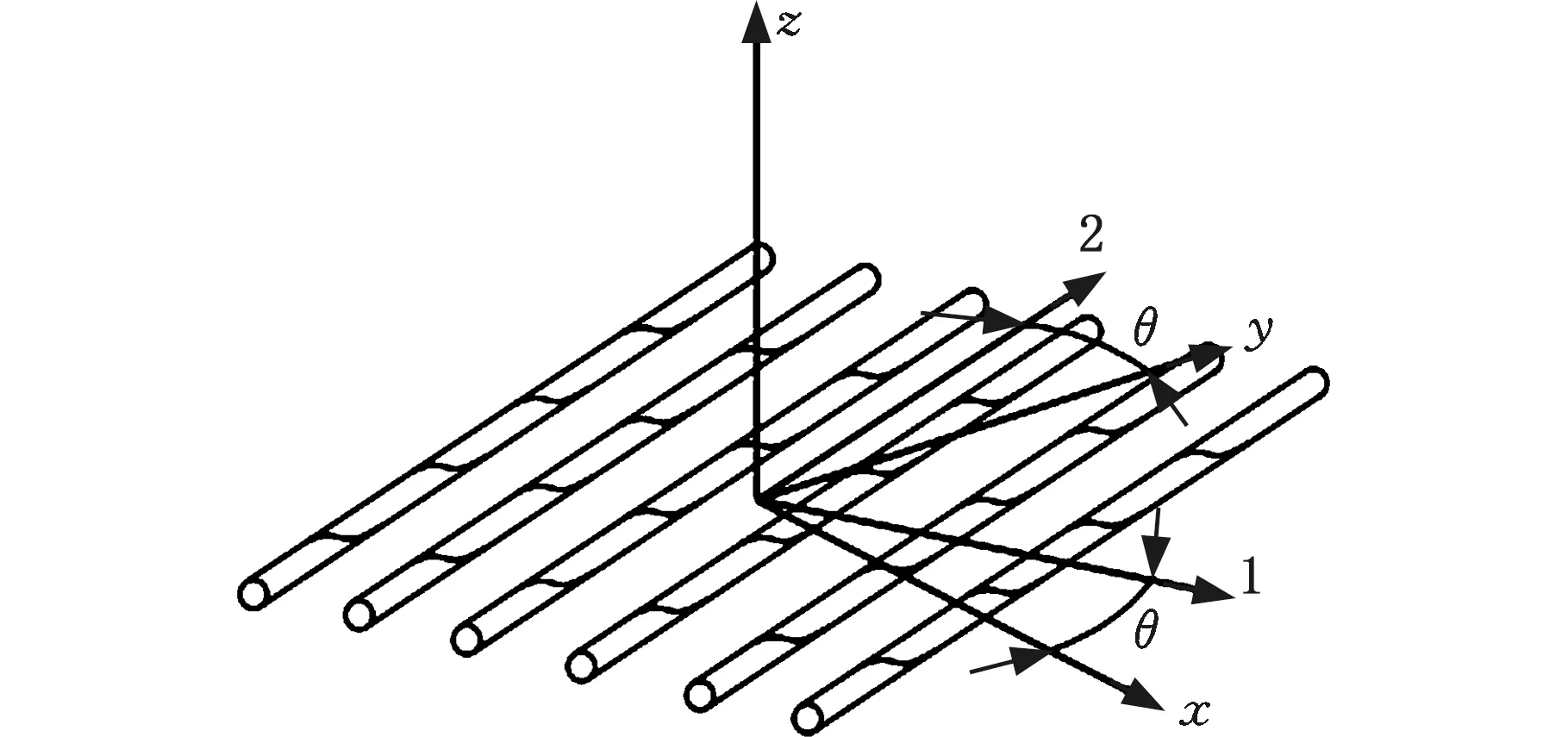
图5 纤维方向与材料主方向夹角示意图Fig.5 Schematic diagram of the angle between the fiber direction and the main direction of the material

(10)

式中,σx为纤维方向的应力;σy为垂直于纤维方向的应力;τxy为纤维平面内剪应力;σ1为材料1方向应力;σ2为材料2方向应力;τ12为材料平面内剪应力;m=cosθ;n=sinθ。

应力应变关系可表示为

(11)

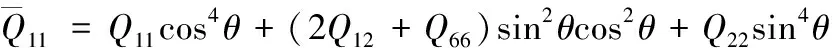
式中,εx为纤维方向的应变;εy为垂直于纤维方向的应变;γxy为单层纤维面内剪切应变;E1、E2、G12、ν12为单层板的四个独立的面内工程弹性常数。

1.4.2层合板弹性性能

如图6所示,层合板由n个单层板粘合而成,取中面为xy坐标平面,z轴垂直板中面,沿z轴正方向依次将各单层编为第1,2,…,n层,层合板中每层的厚度为tk。另层合板的厚度为h,显然有

图6 层合板示意图Fig.6 Schematic diagram of laminate

(12)

第k层上下表面的z坐标分别为zk和zk-1,于是z0=-h/2,zn=h/2。

板内任意一点的位移分量可以表示为

(13)

由直法线不变假设,得

εz=0γzx=0γzy=0

式中,γzx为zx平面的应变;γzy为zy平面的应变。

应变表达式为

(14)

式中,u0(x,y)、v0(x,y)为中面的面内位移分量;w(x,y)为挠度函数,对每一单层都一样。

用矩阵形式表示式(14)为

ε=ε0+zκ

定义作用在单位宽度上复合材料层合板的平均内力N和内力矩M为

(15)

式中,Q为单层纤维刚度矩阵。

由于矩阵ε0和κ中各元素均与z无关,故式(15)可表示为

其中,子矩阵A、B、D均为3×3对称矩阵,矩阵中各元素可按照下式计算:

i,j=1,2,6

2 有限元仿真模型

采用ABAQUS有限元分析软件计算图2所示中心载荷和偏心20 mm载荷状态下FBG传感器位置处的应变值。采用S4R单元类型建立弯曲载荷作用下碳纤维复合材料弹性阶段有限元分析模型,共划分10 240个网格,其中单向0°铺层碳纤维复合材料力学性能如表2所示[26],定义碳纤维复合材料铺层方式为[0°/45°/-45°/90°]s,如图7所示。模型中定义压头和支撑为刚性体,忽略压头与碳纤维复合材料间的摩擦作用,压头与碳纤维复合材料间采用面面接触。

表2 单向碳纤维复合材料性能[26]

图7 纤维铺层方式定义Fig.7 Definition of fiber laying mode

3 结果与讨论

100 N中心加载作用下复合材料的位移变化有限元计算结果如图8所示,可以看出复合材料弯曲变形最大的位置为复合材料中心位置,传感器S1和S2位置处的弯曲变形很小,因此可以忽略FBG传感器弯曲变形引起的信号变化。

图8 100 N中心载荷作用下复合材料位移变化Fig.8 Displacement of composite materials under100 N central load

3.1 中心加载条件

图9所示为中心加载20 N载荷的碳纤维复合材料有限元分析结果,碳纤维复合材料弯曲载荷加载过程中边界条件对称分布,传感器S1和S2关于复合材料结构对称分布,因此由图9可以看出传感器S1和S2对应位置处有限元分析结果一致。提取有限元分析结果中传感器S1对应位置处应变值进行分析,图10所示为5种中心载荷作用下传感器S1对应位置应变变化有限元分析结果,可以看出在载荷施加过程中应变随载荷的增大而线性增大,且传感器S1对应位置处应变值随着载荷的增大而增大。

图9 中心加载条件下应变关于加载位置对称分布Fig.9 Symmetrical distribution of strain with respect to loading position under central loading

图10 5种中心载荷作用下传感器S1对应位置应变有限元分析结果Fig.10 Finite element analysis results of strain at corresponding position of sensor S1 under five central loads

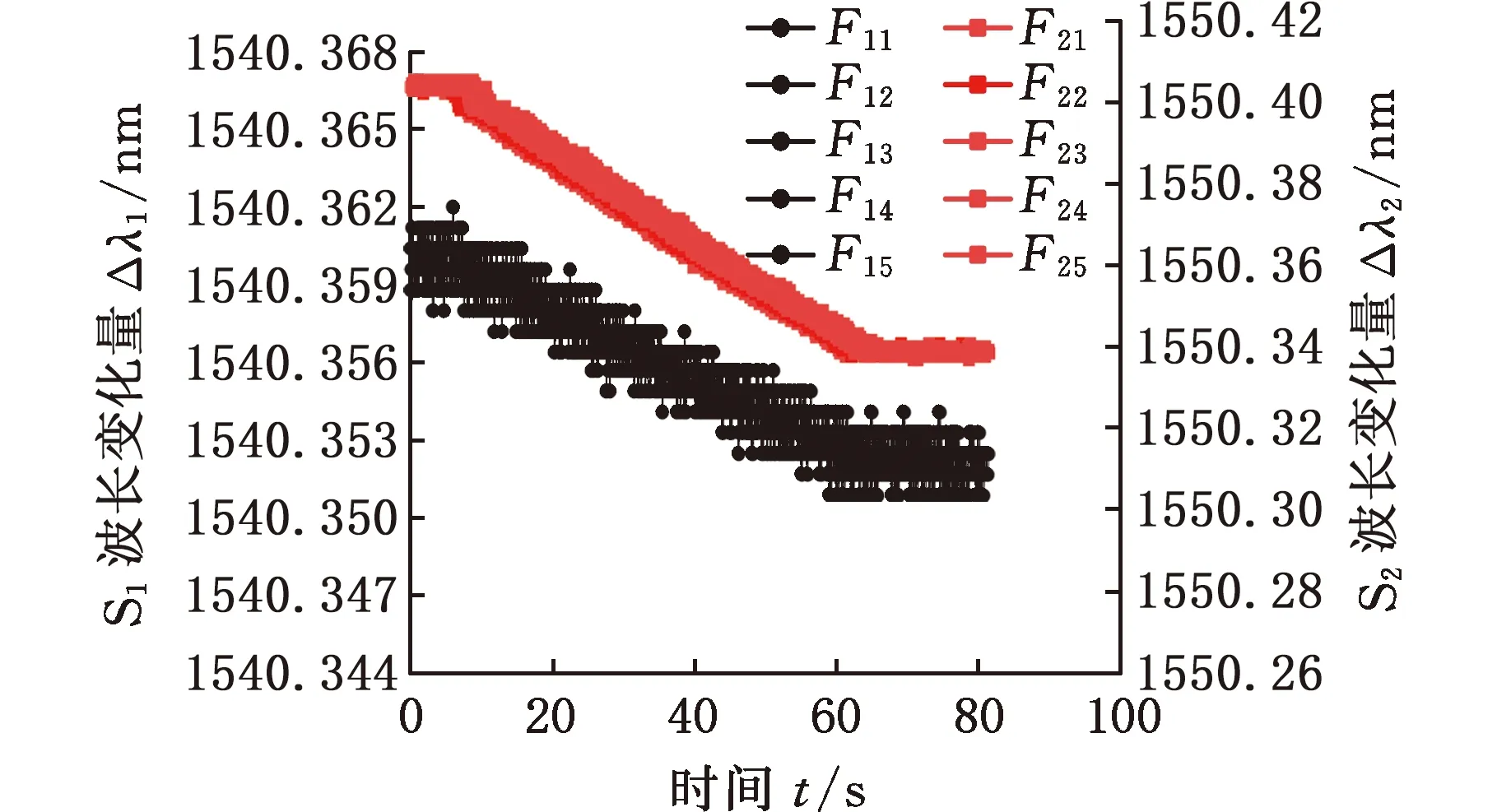
采用表1中5种载荷分别对碳纤维复合材料中心位置进行加载试验,获得图11所示的传感器S1和S2的波长变化量,图中黑色曲线为传感器S1波长变化曲线,红色曲线为传感器S2波长变化曲线,可以看出五种中心载荷作用下,传感器S1和S2的波长呈线性变化且斜率趋于一致,传感器S1和S2的波长变化量随着载荷的增大而增大。同时,由于传感器S1和S2在关于载荷加载位置对称分布,因此S1和S2两传感器的波长变化量相差较小。

(a)20 N载荷作用下S1和S2波长变化值

结合图11中测量得到的波长变化量Δλ,传感器S1和S2的应变值由式(2)计算得到。传感器S1和S2应变测量值与有限元分析值和理论计算值对比如图12所示,可以看出理论计算结果和有限元分析结果一致,验证了有限元模型的有效性;传感器S1和S2测量得到的应变值均小于有限元分析结果,与有限元分析结果和理论计算结果相似的是,随着载荷的增大,FBG传感器对应位置的应变增大;同时,载荷越大FBG传感器测量得到的应变数据分散度越小,因此在进行大载荷监测时FBG传感器获得的数据可靠性越高。

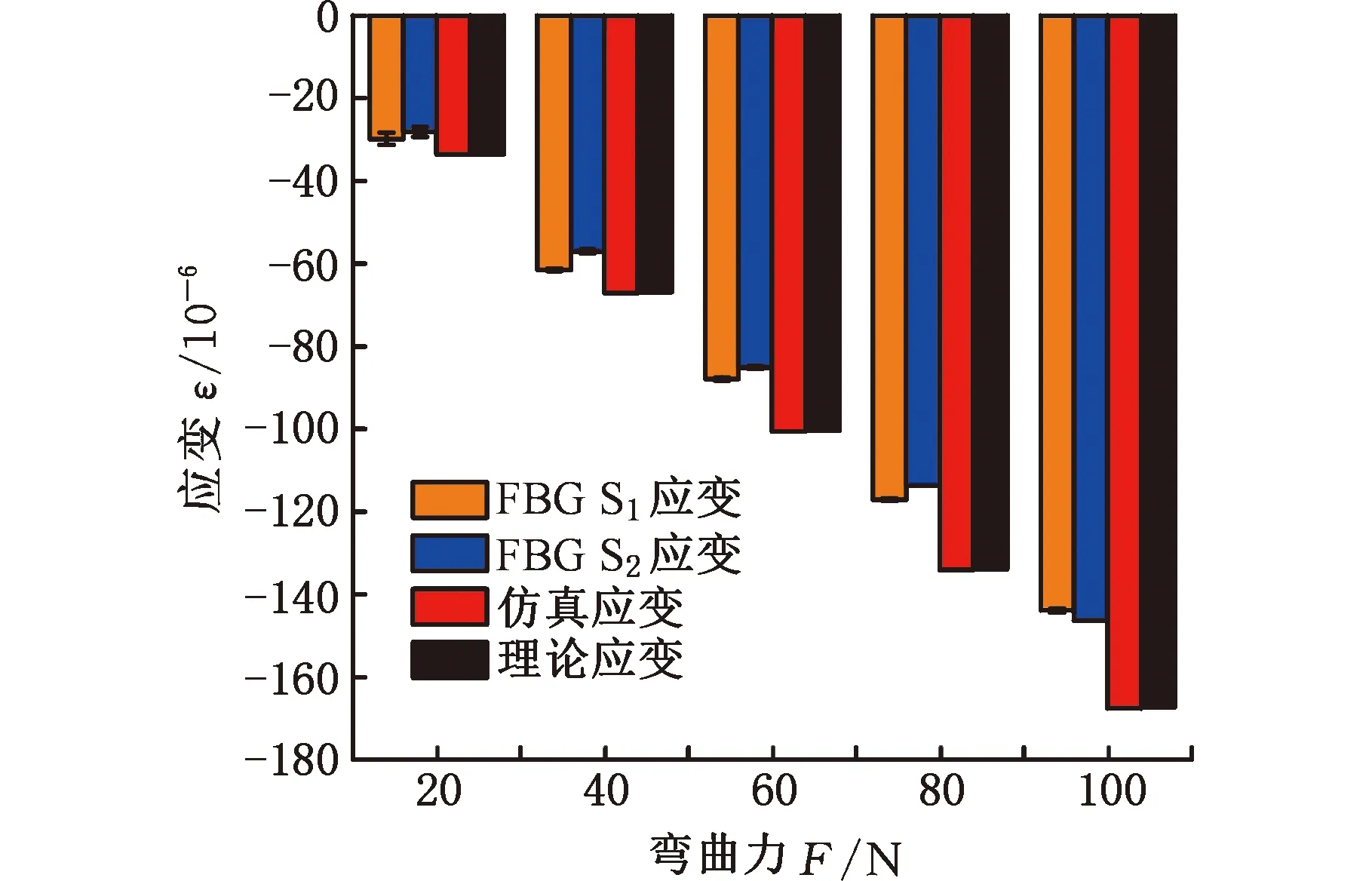
图12 传感器S1和S2应变测量值与有限元分析值和理论计算值对比Fig.12 Comparison of measured strain of sensors S1and S2 with finite element analysis and theoretical calculation values

图13所示为传感器S1和S2测量应变值与理论计算结果的误差对比,黑色曲线为传感器S1的测量误差-载荷关系曲线,红色曲线为传感器S2的测量误差-载荷关系曲线。由于在实际粘贴时难以保证传感器S1和传感器S2的位置,因此两传感器测量的数据有一定偏差,但传感器S1与S2的测量应变与理论计算值的误差随载荷变化趋势一致。随着载荷的增大,传感器S1的测量应变值与理论计算值的误差先增大后减小,最大不超过12.26%,最小可达到9.64%;随着载荷的增大,传感器S2的测量应变值与理论计算值的误差先增大后减小,最大不超过16.22%,最小可达到14.77%;同时,随着载荷的增大,传感器测量应变值与理论计算值的误差离散度越小,数据的可靠性越高。

图13 传感器S1和S2测量应变与理论计算结果误差对比Fig.13 Error comparison between measured strain and theoretical calculation results of sensors S1 and S2

结合式(8)、式(9)以及图11中传感器测量的波长变化量,计算5种中心载荷作用下碳纤维复合材料所受载荷大小以及加载位置,5种中心载荷作用下载荷大小和位置实际值与计算值对比如表3所示,可以看出载荷计算值均大于实际载荷,20～80 N中心载荷作用下载荷位置计算值均大于实际值。

表3 载荷大小和位置实际值与计算值对比

结合表3中数据,载荷大小和位置实际值与图14所示载荷大小和载荷位置实际值与计算值误差分析曲线可以看出,随着载荷的增大载荷计算值与实际值的误差呈现先减小后增大的趋势,载荷误差最大不超过10.37%,80 N中心载荷作用下载荷误差最小可达到7.74%;随着载荷的增大,载荷实际位置与载荷位置计算值误差先减小后增大,载荷位置误差最大不超过2.83%,80 N中心载荷作用下载荷位置误差最小可达到1.17%。结果表明,载荷在20～100 N范围内,采用FBG传感器对碳纤维复合材料所受中心载荷进行监测时载荷大小误差可控制在10.37%内,载荷位置的误差可以控制在2.83%内。

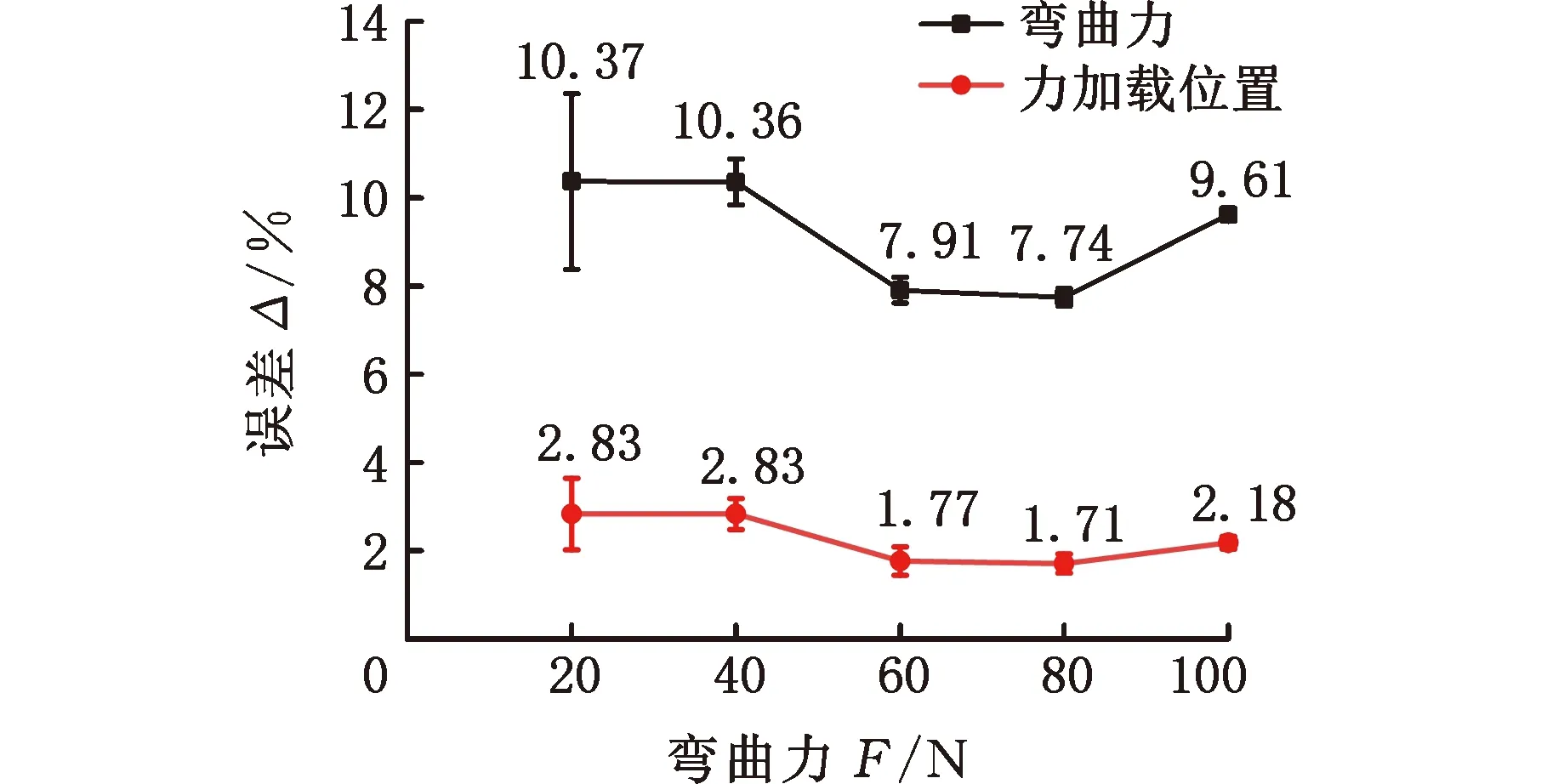
图14 载荷大小和位置实际值与计算值对比Fig.14 Comparison between actual value and calculated value of load size and position

3.2 偏心20 mm加载条件

图15所示为偏心20 mm加载20 N载荷的碳纤维复合材料有限元分析结果。传感器S1和S2关于复合材料结构对称分布,传感器S1和S2对应位置的应变不同,分别提取有限元分析结果中传感器S1和S2对应位置处应变值,图16所示为5种偏心载荷作用下传感器S1和S2对应位置应变变化有限元分析结果。可以看出传感器S1对应位置处应变值明显小于传感器S2对应位置处应变值,且在载荷施加过程中应变随载荷的增大而线性增大,传感器S1和S2对应位置处应变值随着载荷的增大而增大。

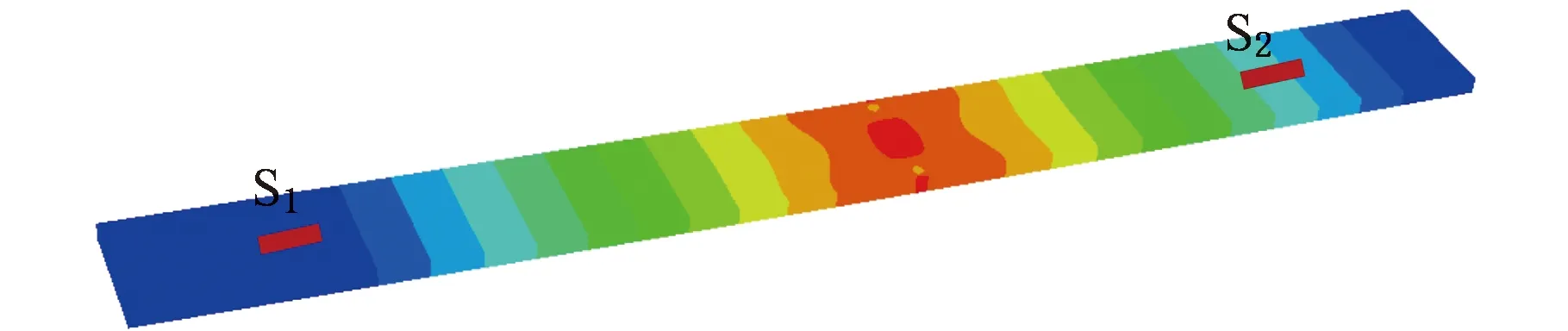
图15 偏心20 mm加载Fig.15 Loading with 20 mm eccentricity

(a)传感器S1对应位置有限元分析结果

采用表1中5种载荷分别对碳纤维复合材料偏心位置进行加载,获得图17所示的传感器S1和S2的波长变化量,图中黑色曲线为传感器S1波长变化曲线,红色曲线为传感器S2波长变化曲线,可以看出5种偏心载荷作用下,传感器S1和S2的波长呈线性变化,且传感器S1和S2的波长变化量随着载荷的增大而增大。传感器S1的波长变化斜率明显小于传感器S2的波长变化斜率,且S1和S2两传感器的波长变化量相差较大。

(a)20 N载荷作用下S1和S2波长变化值

结合图17中测量得到的波长变化量Δλ,传感器S1和S2的应变值由式(2)计算得到。传感器S1和S2应变测量值与理论计算值对比如图18所示,可以看出理论计算结果和有限元分析结果一致,验证了有限元模型的有效性,但传感器S1位置处应变有限元分析值与理论计算值误差较大,传感器S2位置处应变有限元分析值与理论计算值误差较小;传感器S1和S2测量得到的应变值均小于有限元分析值和理论计算值,与有限元分析结果和理论计算结果相似的是,随着载荷的增大FBG传感器对应位置的应变增大;同时,由图18可以看出,除20 N载荷状态下监测的传感器S1和S2应变数据外,载荷越大FBG传感器测量得到的应变数据分散度越小,因此在进行大载荷监测时FBG传感器获得的数据可靠性越高。

(a)传感器S1应变测量值与有限元分析值和理论计算值对比

图19所示为传感器S1和S2测量应变值与理论计算结果的误差对比,黑色曲线为传感器S1的测量误差-载荷关系曲线,红色曲线为传感器S2的测量误差-载荷关系曲线。随着载荷的增大,传感器S1的测量应变值与理论计算值的误差先增大后减小,最大不超过46.70%,最小可达到42.01%;随着载荷的增大,传感器S2的测量应变值与理论计算值的误差先增大后减小,最大不超过10.69%,最小可达到4.53%;同时,随着载荷的增大,传感器测量应变值与理论计算值的误差离散度越小,数据的可靠性越高。与有限元分析结果一致的是,传感器S1位置处应变值远小于传感器S2处应变值。由于传感器S1位置处的应变值较小导致传感器S1测量结果误差远大于传感器S2位置处的应变误差值,因此以传感器S2处的误差值为准。

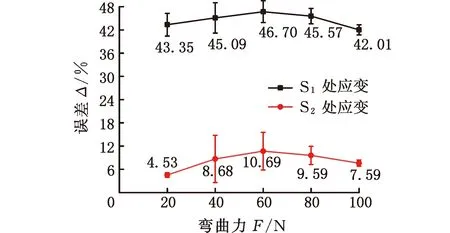
图19 传感器S1和S2测量应变与理论计算结果误差对比Fig.19 Error Comparison between measured strain and theoretical calculation results of sensors S1 and S2

结合式(8)、式(9)以及图17中传感器测量的波长变化量,计算5种偏心载荷作用下碳纤维复合材料所受载荷大小以及加载位置,5种偏心载荷作用下载荷大小和位置实际值与计算值对比如表4所示,可以看出载荷计算值均大于实际值,载荷位置计算值均大于实际载荷位置。

表4 载荷大小与位置计算值与实际值

结合表4中数据、载荷大小和位置实际值与图20所示载荷大小和载荷位置实际值与计算值误差分析曲线可以看出,随着载荷的增大,载荷计算值与实际值的误差呈现先减小后增大的趋势,载荷误差最大不超过13.89%,60 N载荷作用下载荷误差最小仅有8.05%;随着载荷的增大,载荷位置的实际值与计算值之间的误差呈现先增大后减小又增大的波动性,载荷位置误差最大不超过5.70%,20 N偏心载荷作用下载荷位置误差最小仅有3.04%。结果表明,载荷在20～100 N范围内,采用FBG传感器对碳纤维复合材料所受偏心载荷进行监测时载荷大小误差可控制在13.89%内,载荷位置的误差可以控制在5.70%内。

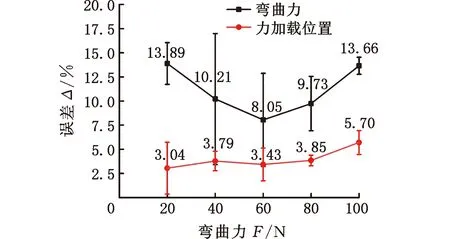
图20 载荷大小和位置实际值与计算值对比Fig.20 Comparison between actual value and calculated value of load size and position

4 结论

推导了复合材料弯曲载荷作用下应变计算模型,结合理论模型验证了有限元模型的正确性,采用光纤光栅(FBG)传感器在线监测技术,研究了复合材料弯曲载荷大小和载荷施加位置的实时监测方法,该方法可实现复合材料部件工作过程中关键载荷信息的实时监测。主要结论如下:

(1)通过在碳纤维复合材料构件表面粘贴FBG传感器可实现碳纤维复合材料载荷状态的实时监测,及时反馈碳纤维复合材料构件所受载荷的大小和载荷位置信息。

(2)采用FBG传感器对碳纤维复合材料进行中心加载时,在20～100 N载荷范围内,载荷误差小于10.37%,加载位置误差小于2.83%。

(3)采用FBG传感器对碳纤维复合材料进行20 mm偏心加载时,在20～100 N载荷范围内,载荷误差小于13.89%,加载位置误差小于5.70%。