基于梯度提升决策树的冷轧高强钢卷力学性能预测

王 伟 马乾伦 白振华 王子昂

1.福州大学机械工程及自动化学院,福州,3501002.燕山大学机械工程学院,秦皇岛,066004

0 引言

冷轧高强钢卷是结构轻量化的重要材料,它表面质量好、尺寸精度高、机械性能强,广泛应用于汽车制造、航空和精密仪器等众多领域[1-2]。力学性能是高强钢的关键质量指标之一,退火工艺是力学性能调控的重要手段,而力学性能预测可建立工艺因素与性能之间的定量关系,为退火工艺调控提供基础[3-5]。

传统性能预测建模方法是根据物理冶金过程分析建立组织模型,再由组织模型建立性能预测模型[6-7],但带钢生产冶金流程长,工艺参数较多,导致建模过程复杂,成本高。随着智能制造技术的发展,基于大数据分析的力学性能预测建模方法开始被用于钢铁生产,而应用各种人工智能算法通过化学成分和相关工艺参数建立性能预测模型是目前研究的重点方向[8-10]。

神经网络模型是目前应用最广泛的带钢性能预测模型。LALAM等[11]提出前向反馈人工神经网络,根据冷轧钢卷的化学成分和工艺参数来预测力学性能,在允许误差范围内,屈服强度和极限抗拉强度预测准确率达到了90%,符合用户对产品的要求。ORTA等[12]利用神经网络模型和3537条冷轧双相(dual phase,DP)钢生产数据进行力学性能预测,得到的DP钢屈服强度、抗拉强度和伸长率预测模型的平均绝对误差分别为2.69%、2.00%、5.84%,但是由于建模时神经元个数与隐藏层个数的选择更多时候依赖于实践经验,造成了神经网络模型开发周期长,超参数调优困难。

集成学习可以将多个基模型结合在一起建立集成学习模型,集成学习模型可以解决很多单个模型无法解决的复杂机器学习问题[13]。李飞飞等[14]采用BP神经网络对样本间的偏差进行建模,建立了大量的样本偏差神经网络分离器,并将子模型与具有强泛化能力的Bagging集成学习算法进行融合,得到延伸率在绝对误差±5%下的预测精度达到了99.48%,但该方法计算量较大。王显鹏等[15]以Bagging集成学习方法为基础,结合适应性提升(AdaBoost)集成学习的误差较大样本重点学习策略,提出了一种带钢产品质量在线预测混合集成学习方法,结果表明该混合集成学习方法的泛化能力和预测精度优于Bagging和AdaBoost两种集成学习方法。

梯度提升决策树(gradient boosting decision tree,GBDT)算法[16]是一种应用非常广泛的集成学习算法,它基于 Boosting迭代思想,通过不断拟合残差来提升性能。苏兴华等[17]采用GBDT模型对钻井机械钻速建立预测模型,并与支持向量机、逻辑回归以及K最近邻方法进行比较,结果表明,GBDT算法相比于其他算法具有较高的准确率。

冷轧高强带钢是高附加值的产品,具有性能控制要求高、性能预测难的特点。本文以1180 MPa级超高强度冷轧DP钢为例,利用工艺和力学性能生产数据样本,建立GBDT模型、BP模型、广义可加模型(generalized additive models,GAM)并进行比较;为提高断后伸长率模型预测精度,研究了考虑误差补偿的断后伸长率预测模型,建立了模型预测误差GBDT分类模型和考虑误差补偿的模型预测修正方法并对生产实际预测精度进行了分析。

1 力学性能预测模型建立

1.1 数据获取及处理

冷轧钢卷生产过程包括钢坯加热、热轧、酸轧、连续退火、平整工序,与性能相关的参数包括钢卷化学成分、产品规格参数和工艺参数。其中化学成分包括C、Si、Mn、P、S、Cu、Ni、Cr、Mo、Nb、Ti、B、N、Al共14个;钢卷规格参数包括钢卷宽度、冷卷厚度和热卷厚度;工艺参数包括钢坯加热出炉温度、终轧温度、卷曲温度、连退过程加热段温度、均热段温度、缓冷段温度、快冷段温度、机组速度和平整过程平整率,共12个。

钢卷力学性能包括屈服强度、抗拉强度、断后伸长率,表1为该钢种力学性能统计表,可以看出,该钢种屈服强度和抗拉强度很高而断后伸长率较低。

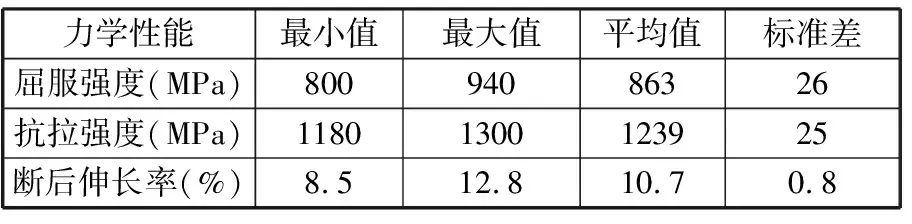
表1 力学性能统计表

用于性能预测的成分、工艺参数来自于生产过程的测量值,这些值存在噪声和异常值,利用3σ准则进行数据清洗。清洗后与性能相关的参数有26个,其中12个产品规格和工艺参数是独立变量,而化学成分与性能的影响有一定相关性。为描述性能与成分的关系,传统冶金机理的性能模型常用碳当量的概念,本文利用大数据[18]主成分分析(principle component analysis, PCA)技术对化学成分进行降维,降维后的化学主成分之间更加独立,可降低成分中冗余信息,从而实现化学成分特征的有效提取。

1.2 化学成分PCA降维及结果分析

为了消除量纲的影响,进行主成分分析之前,对化学成分数据采用中心对称的标准化处理,标准化公式为

(1)

式中,x*为标准化后的数据;x为待标准化数据;μ为数据均值;σ为数据标准差。

PCA的步骤如下:

(1) 计算样本数据的协方差矩阵:

(2)

(2)求解C的特征值λf及其单位正交的特征矢量pf:

λfpf=Cpf

(3)

对特征值排序,前h个较大的特征值λ1,λ2,…,λh(λ1≥λ2≥…≥λh>0)表示主成分的方差,λf对应的特征矢量pf就是第f个主成分的系数。在PCA中,主成分中信息量的大小由累积方差贡献率(cumulative percent variance,CPV)表示:

(4)

一般认为φCPV大于85%即可。经过主成分分析得到化学成分累积贡献率如图1所示。为避免丢失原始数据的重要信息,并且选入较少的噪声,选取累积方差贡献率约为92%,有利于提高模型性能[19]。

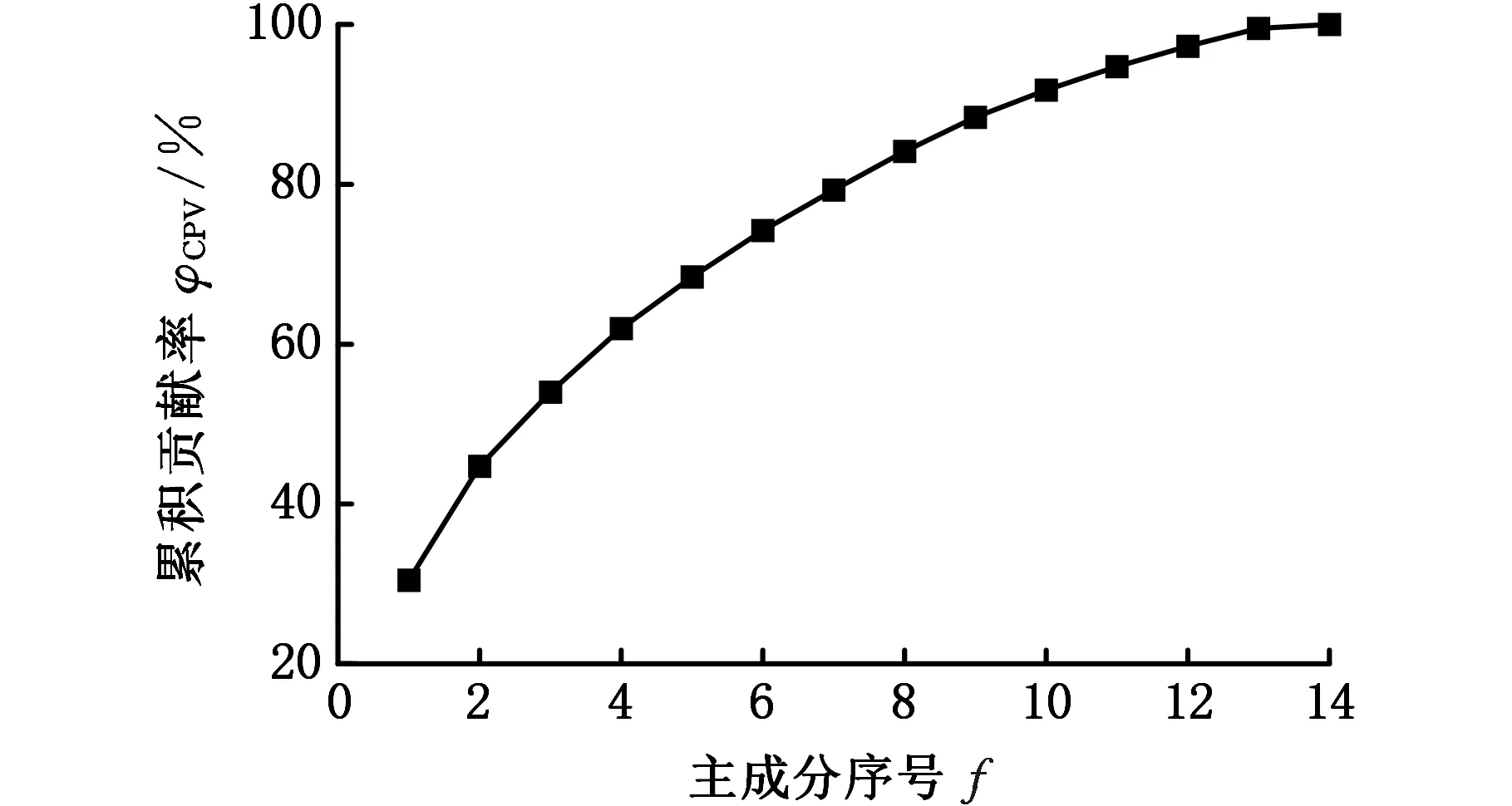
图1 化学成分数据累积贡献率Fig.1 Cumulative contribution rate of chemical composition data

根据以上分析,化学成分主成分数目取10,然后将12个工艺参数进行标准化处理,再与10个化学成分主成分特征组合,可得到性能模型输入的22个特征参数。

1.3 GBDT回归算法建模过程

GBDT回归算法的实现过程如下:

输入训练集T={(x1,y1),(x2,y2),…,(xi,yi),…,(xN,yN)},其中xi∈X⊆Rn,X为输入样本空间;xi为钢卷输入特征;yi∈Y⊆R,Y为钢卷力学性能。

(1)初始化第一个学习器f0(x):

(5)

式中,L(yi,c)为损失函数;c为使损失函数最小化的常数。

(2)建立M棵分类回归树(m=1,2,…,M)。

①对样本i计算第m棵树对应的伪残差:

(6)

②利用回归树拟合数据(xi,rm,i)得到第m棵树对应的叶节点区域Rm,j,其中,j=1,2,…,Jm,且Jm为第m棵回归树叶子节点的个数。

③对j计算最佳拟合值:

(7)

④更新强学习器fm(x):

(8)

式中,I(x∈Rm,j)为示性函数,样本观测点落入Rm,j区域,函数为1,否则为0。

(3)得到最终强学习器fM(x)的表达式:

(9)

2 力学性能预测建模结果与分析

2.1 模型数据集划分

原始数据经过数据处理之后,得到5205条高质量数据,首先按照7∶3的比例,采用同分布抽样方法划分为3643条建模数据集和1562条测试集,图2为建模数据集和测试集屈服强度高斯核密度分布曲线,该图表明建模数据集和测试集分布几乎完全一致。抗拉强度以及断后伸长率采用同样方法划分数据集。其次采用交叉验证法对建模数据集进行划分[20],这里采用5折交叉验证法,将建模数据集分成5个数据子集,每次选择1个子集作为验证集,其余4个子集作为训练集用于训练模型,执行5次模型训练,得到5个模型,选取验证集精度最好的模型作为预测模型,这种训练方式数据利用率达100%。每个模型的验证集未参与训练,验证集精度是未知样本的预测精度,反映了模型的泛化能力,利用验证集预测精度进行模型评估,能够有效防止过拟合和欠拟合现象,提高模型鲁棒性。

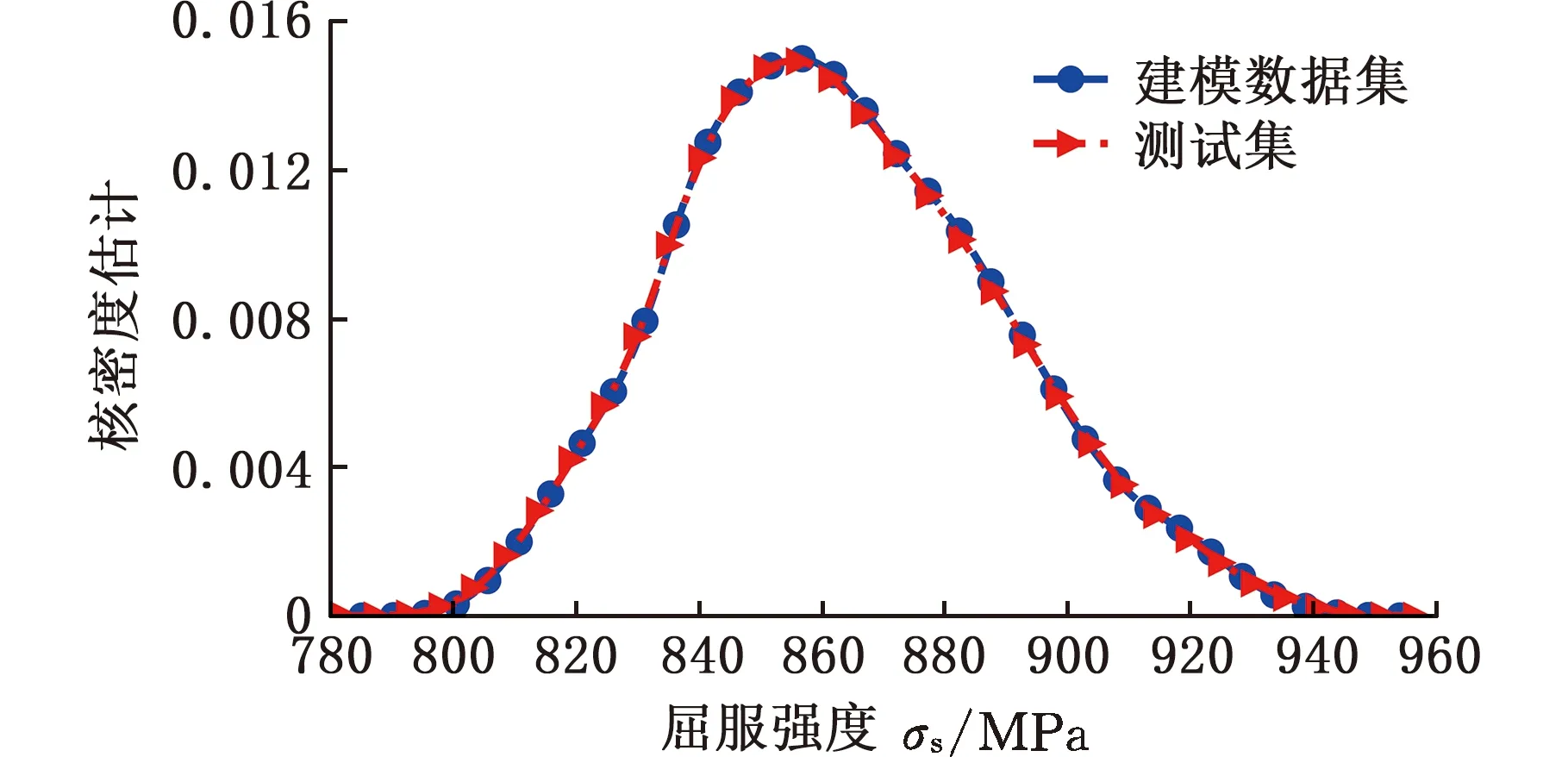
图2 屈服强度高斯核密度分布曲线图Fig.2 Gaussian kernel density distribution curve of yield strength

2.2 模型参数优化

GBDT模型、BP模型和GAM模型中的超参数对模型的精度和泛化能力有重要影响,其中影响GBDT模型的主要超参数有学习率、决策树数目、决策树深度;BP模型主要影响参数包括隐藏层数目、隐藏层节点个数、最大迭代次数、正则化参数、激活函数;GAM模型主要超参数包括最大迭代次数、精度。

超参数调优的方法主要有随机搜索法、网格搜索法、贝叶斯优化方法,其中网格搜索方法是穷举搜索方法,具有优化解全局性好的优点。考虑本研究的钢种数据规模,本文选择网格搜索法进行超参数调优。

三种模型经超参数调优后,GBDT模型最佳超参数为:学习率0.309,决策树个数500,决策树最大深度5;BP模型选用单隐层,隐藏层节点个数为54,最大迭代次数为600,正则化参数alpha为0.0001、采用Relu激活函数;GAM模型最大迭代次数为100,精度为0.000 01。

2.3 力学性能预测模型的比较与分析

构建力学性能模型过程中,采用一些评估指标用于反映模型的预测性能,回归预测一般采用均方根误差(root mean squared error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)作为评估指标:

(10)

(11)

(12)

式中,R为总样本数;yr为实测值;pr为预测值。

根据生产对DP钢力学性能预测模型精度的要求,屈服强度、抗拉强度和断后伸长率预测准确率需达到92%,其中屈服强度的绝对误差要求在±35 MPa之内,抗拉强度的绝对误差要求在±30 MPa之内,断后伸长率的绝对误差要求在±0.9%之内。利用网格搜索和交叉验证方法可以得到预测集精度最好的力学性能模型。表2所示为钢卷力学性能的预测精度。由表2可以看出:

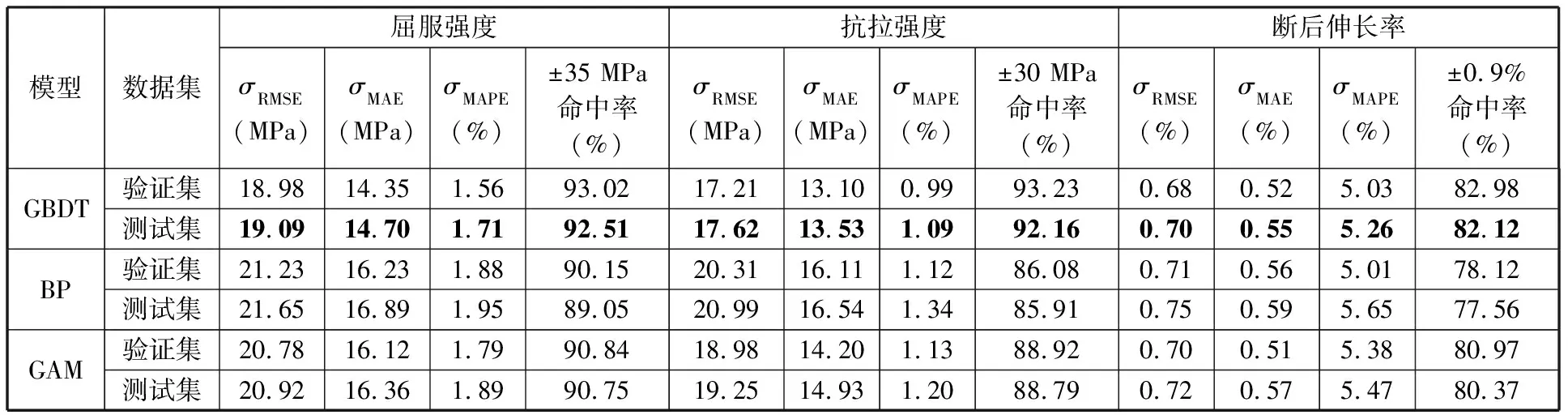
表2 力学性能预测精度

(1)GBDT模型验证集和测试集精度都高于BP模型和GAM模型验证集和测试集精度,并且测试集与验证集误差接近,表明GBDT模型精度高,对未知数据泛化能力强;

(2)精度最高的GBDT模型预测的屈服强度有92.51%的样本数据绝对误差在±35 MPa范围内;预测的抗拉强度有92.16%的样本数据绝对误差在±30 MPa范围内。屈服强度和抗拉强度的预测精度达到命中率92%的生产要求。

(3)82.12%的样本数据断后伸长率GBDT模型预测绝对误差在±0.9%范围内,与命中率92%的要求有一定差距。该钢种力学性能具有强度高韧性较低的特点,加大了钢卷性能取样试验难度,也一定程度上加大了断后伸长率预测的难度。

3 模型预测误差估计与模型修正方法

为进一步提高该钢种的断后伸长率预测精度,建立模型预测误差分类模型,通过对模型预测值误差补偿来提高模型预测精度,该方法流程如图3所示。首先计算样本训练集的性能模型预测误差,建立预测误差样本训练集,然后按预测误差不同级别对误差样本训练集进行误差分类,通过机器学习分类算法建立预测误差分类预测模型。

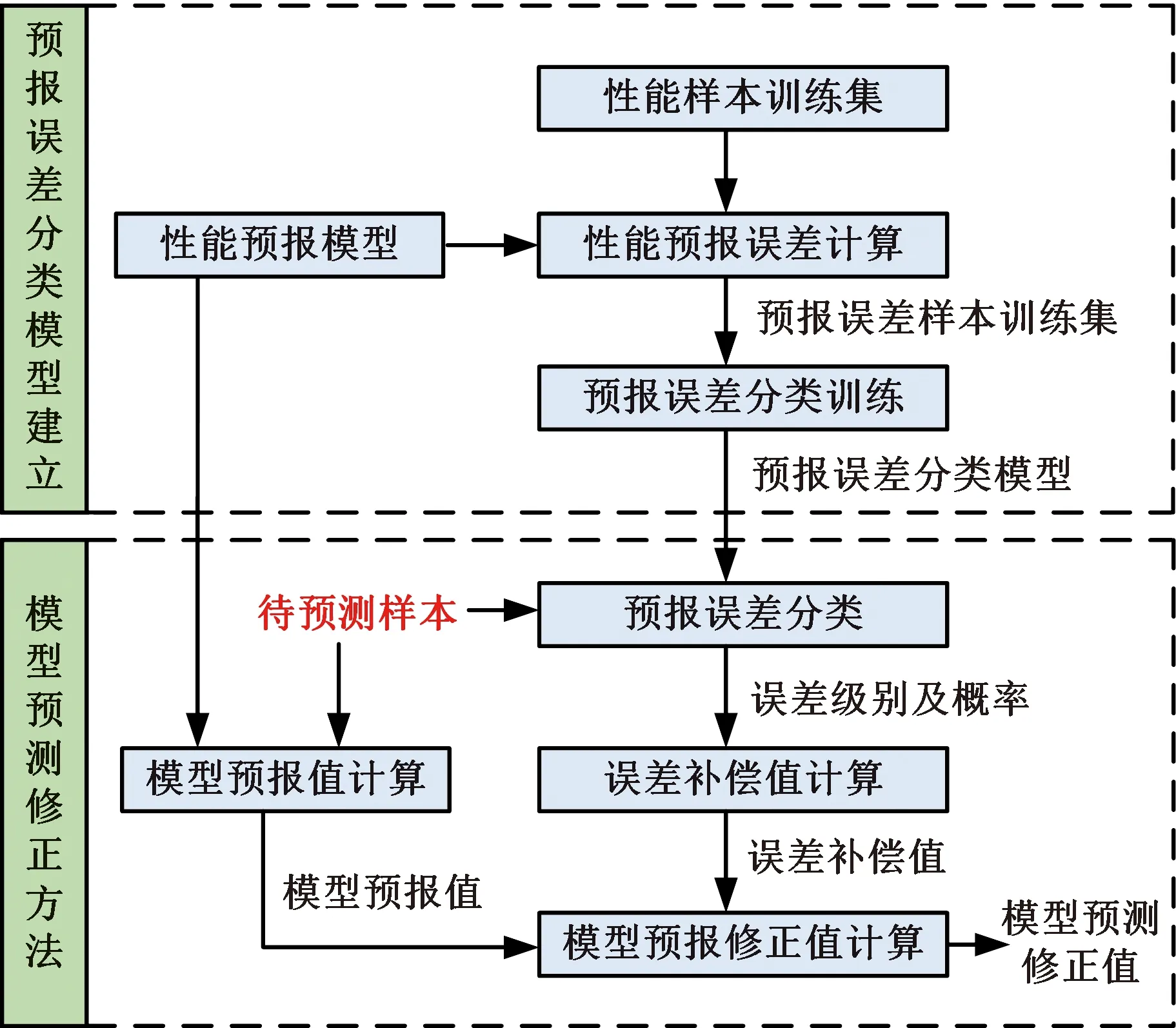
图3 误差分类模型建立与考虑误差补偿的模型预测修正流程图Fig.3 The establishment of error classification model and the principle of model prediction and correction considering error compensation

在性能预测时,对待测样本输入性能预测模型进行模型预测值计算,得到模型预测值;同时,对待测样本输入预测误差分类模型进行预测误差分类计算;最后根据误差级别及概率计算预测误差补偿值,利用误差补偿值对模型预测值进行修正得到模型预测修正值。

3.1 预测误差分布的GBDT分类模型

3.1.1GBDT分类模型

建立误差分类预测模型的目的是求出预测模型的预测结果属于各误差级别的概率,因此,需要建立一个可以用于求解多分类概率分布的模型。GBDT算法除了可以用于回归学习外也可以进行分类学习,并且已经得到了广泛应用。如刘金元等[21]考虑航班延误状态特征对航班延误的影响,构建了GBDT航班延误预测分类模型,并将分类结果与支持向量机和随机森林分类算法进行比较,结果表明GBDT分类算法具有更高的预测准确度。GBDT分类算法可以用来研究该类问题。

以样本的误差区间作为GBDT分类模型的监督目标,利用模型对样本的误差区间进行预测。GBDT分类模型在解决二分类问题及多分类问题上应用广泛,考虑到多类别预测难度增加,本文采用GBDT二分类模型,建立多个分类器来解决多分类问题。

GBDT分类算法输入数据集为T={(x1,y1),(x2,y2),…,(xi,yi),…,(xN,yN)}。xi为影响性能的特征;yi为类别标识,yi∈{0,1},其中,1代表正类,0代表负类。

GBDT分类算法实现流程与GBDT回归算法类似,包括初始化学习器、分类回归树生成、基于分类回归树的强化学习器建立,其中学习器初始化方程、伪残差计算式、最佳拟合值计算式分别如下:

(13)

(14)

(15)

式中,P(Y=1|x)为训练样本中y=1 的比例。

利用最佳拟合值cm,j得到GBDT分类的强化学习器fM(x),再利用强化学习器计算得到分类概率值,概率值计算表达式为

(16)

3.1.2预测误差GBDT分类模型建立

性能预测模型是对力学性能的回归预测,得到的预测误差是连续型变量,为了建立误差分类预测模型,需要对预测误差进行离散化处理。考虑建立误差分类模型时能获得更精确的概率分布,本文将断后伸长率预测误差以0.8%为区间,划分为∈(∞,-2.0]、(-2.0,-1.2]、(-1.2,-0.4]、(-0.4,0.4]、(0.4,1.2]、(1.2,2.0]、(2.0,+∞)共7个误差级别,级别代号分别为-2.0,-1.6,-0.8,0,0.8,1.6,2.0。

将数据样本集的断后伸长率预测结果按误差区间划分确定误差级别,原样本训练集的预测误差级别作为训练集,测试集为原待测样本,进行每个误差级别的GBDT二分类模型训练与测试。

预测误差分类模型训练过程如下:

(1)模型预测误差级别标签生成。对于每一个误差级别,根据样本预测误差和误差级别的设定范围,采用One-Hot独热编码方法,生成样本的误差级别标签,其中预测误差属于该级别的样本标记为正类(1),不属于的样本标记为负类(0),从而建立7个误差级别对应的模型预测误差分类的训练集。

(2)利用模型预测误差分类的训练集和GBDT二分类算法建立误差级别的预测误差二分类模型hk(x),k为误差级别序号。

(3)重复上述过程,便可以得到7个二分类模型{h1(xi),h2(xi),…,h7(xi)}。

预测误差分类模型测试过程为:取出待测样本xi,分别投入7个二分类模型中进行计算,从而可以得到计算结果{P1,P2,…,P7},这7个概率值表征了性能模型的预测结果可能落在某个误差级别的概率,从而得到待测样本xi的模型预测误差分布。

3.2 考虑误差的模型预测修正计算

利用训练好的断后伸长率误差分类模型可以对断后伸长率回归模型的预测结果进行误差补偿,以提高断后伸长率预测精度。具体步骤如下:

(1)将待预测的钢卷模型输入参数代入断后伸长率GBDT回归模型,得到断后伸长率预测值δGBDT;

(2)将待预测的钢卷模型输入参数代入7个误差级别的二分类模型,得到该样本属于每种误差级别的概率Pδ,k,k=1,2,…,7;

(3)根据误差级别划分范围,设每个级别的平均误差Δm,k分别为-2.0,-1.6,-0.8,0,0.8,1.6,2.0。将平均误差Δm,k与对应的误差级别概率Pδ,k相乘,再将这些乘积相加得到误差补偿值:

(4)断后伸长率GBDT预测值δpred=δGBDT-Δδ。

取预测误差测试集中的一个样本作为误差补偿修正算例,该样本的断后伸长率实测值为10.2%,模型预测值为10.62%,误差级别为0.8级。将该样本参数代入7个误差级别二分类模型,得到图4所示的误差级别概率分布图,对应0.8级概率最大。将误差级别的平均误差与对应的误差级别概率相乘并求和,可以得到样本预测误差补偿值为0.32%,模型预测值减去补偿值后,得到模型预测修正值为10.3%。

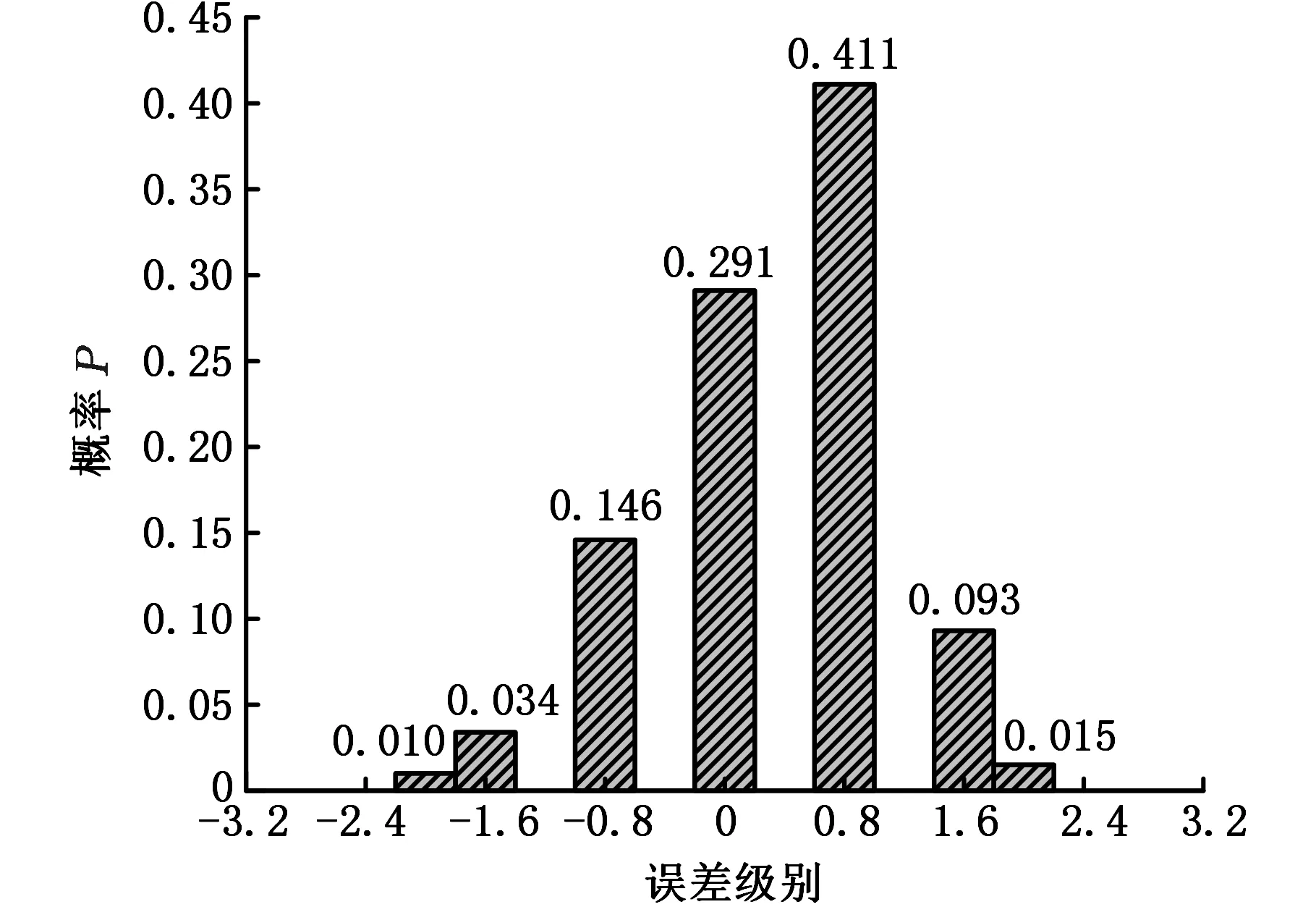
图4 测试样本在各误差级别的概率预测结果Fig.4 The probability prediction results of the test sample at each error level

3.3 模型预测修正算法结果及分析

3.3.1误差补偿后模型测试集精度分析

断后伸长率预测模型误差补偿前后的预测精度如表3所示,结果表明,原预测模型经过误差补偿后,测试集有94.63%的样本数据绝对误差在±0.9%范围内,符合用户要求。

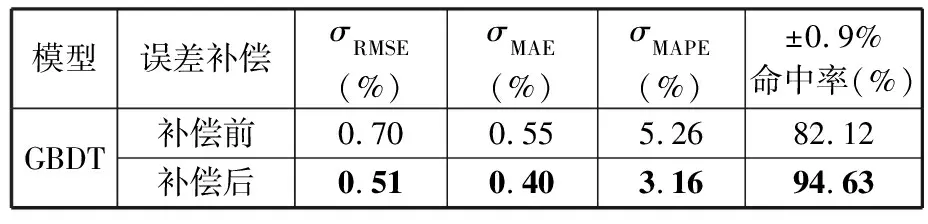
表3 断后伸长率误差补偿后预测精度

为了观察断后伸长率经过误差补偿前后的预测值与实测值之间的分布情况,对测试样本误差补偿前后的预测值进行了可视化分析。图5和图6分别为测试样本经过误差补偿前后的预测值与实测值的散点图,图中虚线表示断后伸长率的误差界限(±0.9%),可以看出,经过误差补偿之后,预测精度明显提高。

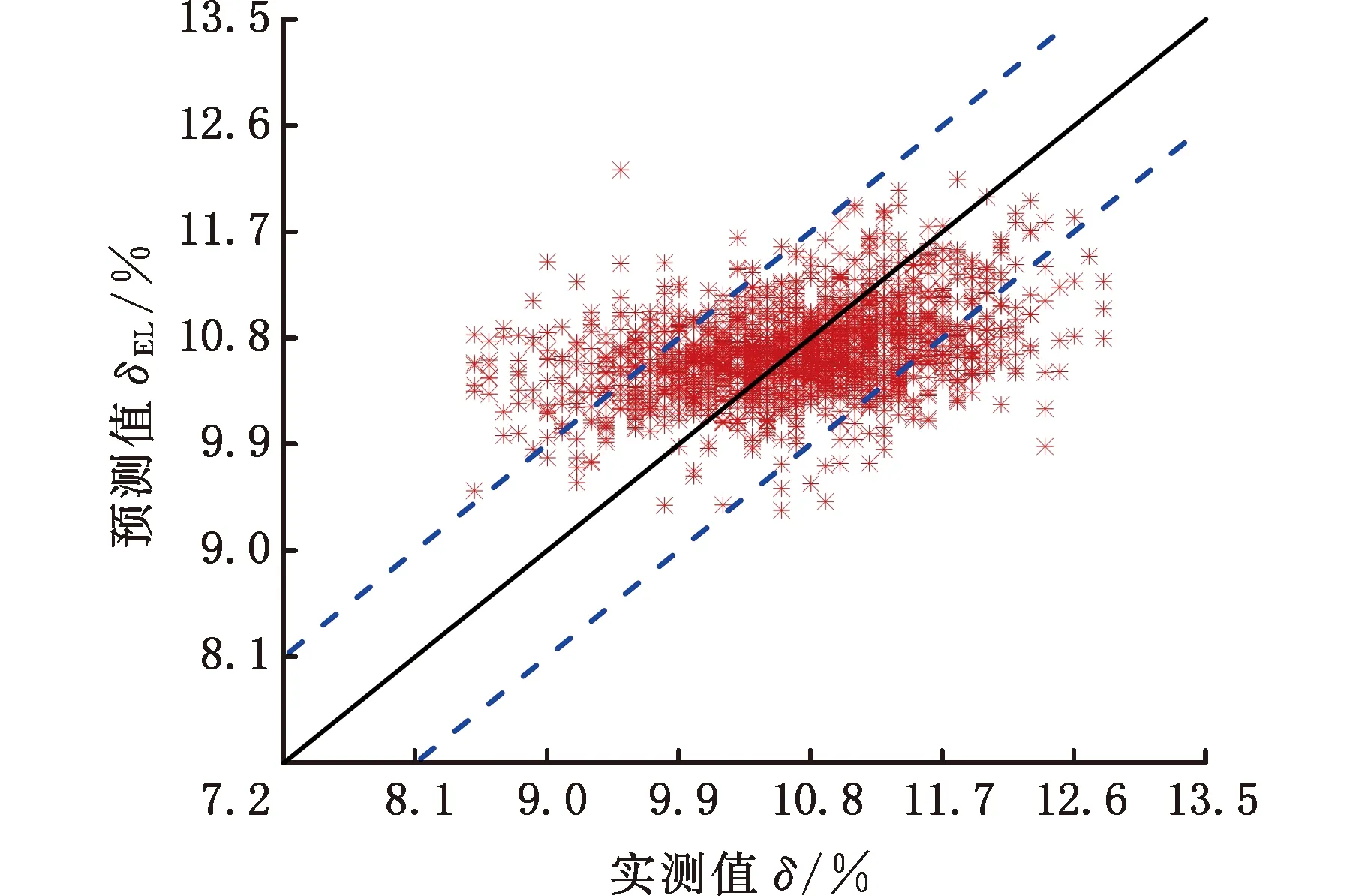
图5 断后伸长率实测值与未补偿的模型预测值对比Fig.5 Comparison of measured elongation after fracture with uncompensated model predicted value

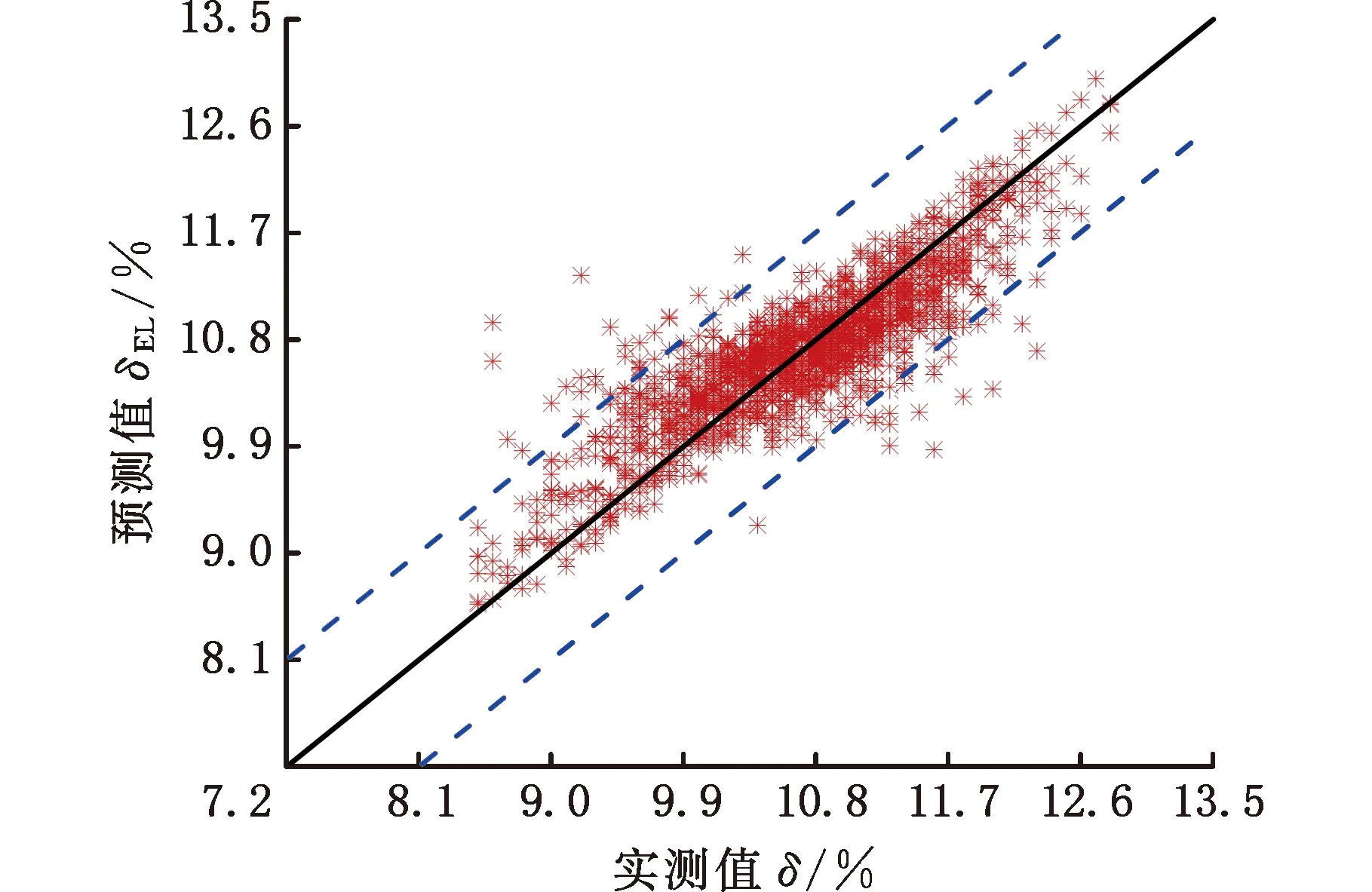
图6 断后伸长率实测值与误差补偿后预测值对比Fig.6 Comparison of measured elongation after fracture with predicted value after error compensation

为了更加直观地观察断后伸长率的实测值与经过误差补偿后的预测值之间的关系,图7展示了测试样本中随机的100条经过误差补偿后的数据的预测误差分布示意图。其中δmean表示样本的预测误差的均值,δmean+Δδ表示样本预测误差所允许的最大值,δmean-Δδ表示样本预测误差所允许的最小值。从图中可以看出,在这100个测试样本中,93%的样本的预测误差在误差允许区间内,说明断后伸长率预测值经过误差补偿后,原模型的预测精度得到了一定的提高。

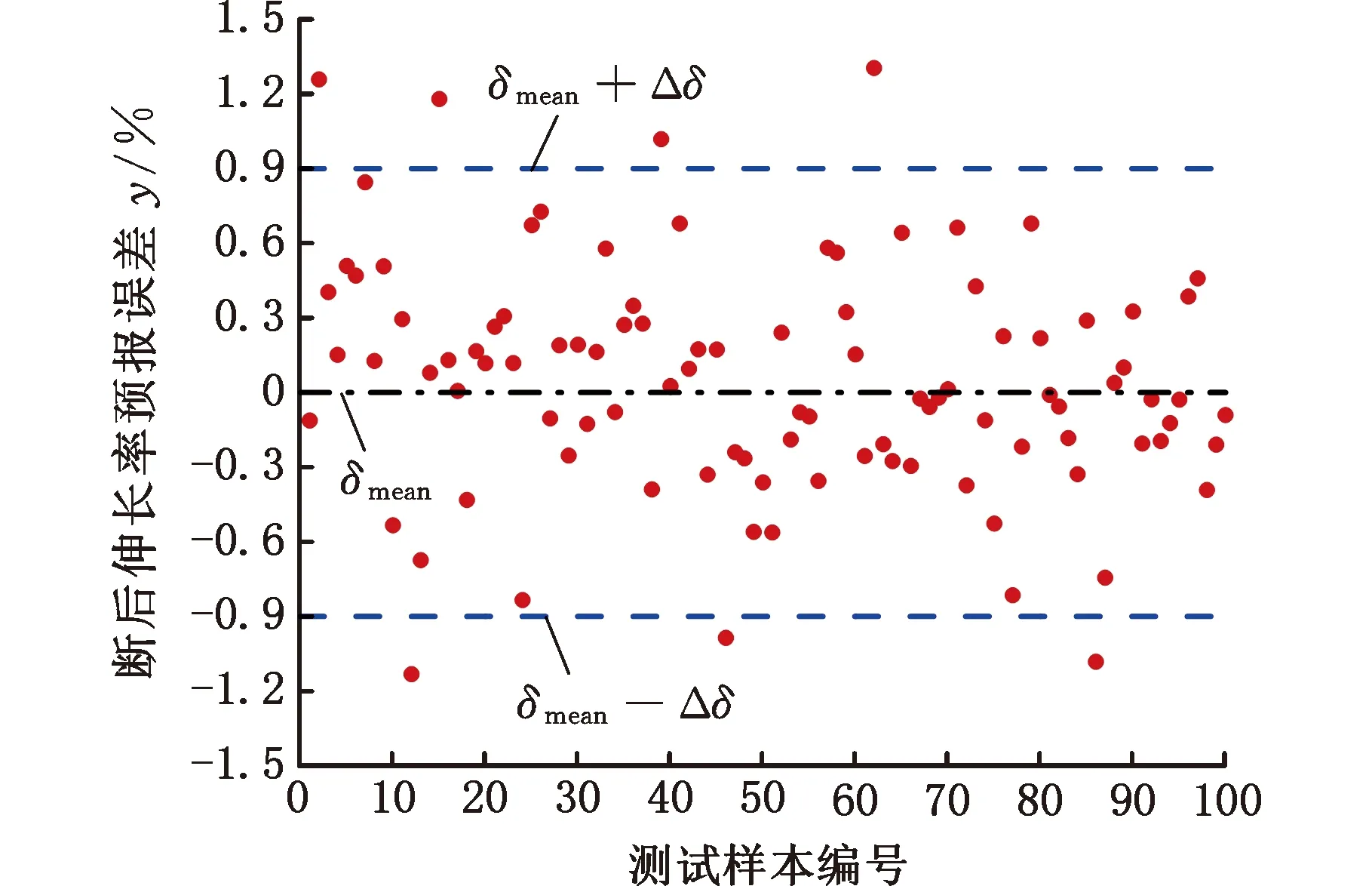
图7 断后伸长率误差补偿后预测误差示意图Fig.7 Prediction error diagram after elongation error compensation

3.3.2生产实绩预测精度分析

为了进一步验证该模型在生产过程中对未知样本的预测精度,将生产中从未参加任何模型训练与预测的400条测试样本代入性能预测模型。图8所示为测试样本预测值与实测值的比较,图中虚线表示性能误差界限,预测结果的准确率超过了92%。

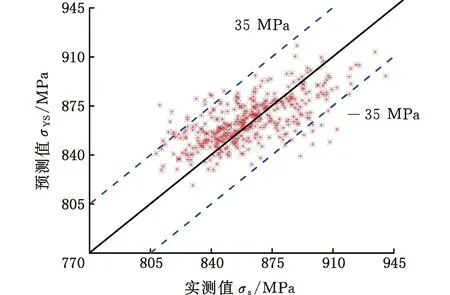
(a)屈服强度实测值与预测值对比

4 结论

针对双相(DP)高强钢开展性能预测研究,可得到如下结论:

(1)采用化学主成分代替化学成分并结合规格和工艺参数归一化,减少了模型输入特征参数数目。

(2)通过模型超参数调优、交叉验证、数据集同分布抽样,可以有效地避免过拟合的产生,提高了模型的泛化能力;比较性能预测梯度提升决策树(GBDT)模型、BP神经网络模型和广义可加模型(GAM)预测精度,结果表明GBDT模型精度最高。

(3)利用GBDT回归模型,预测的屈服强度有92.51%的样本数据绝对误差在±35 MPa范围内,预测的抗拉强度有92.16%的样本数据绝对误差在±30 MPa范围内;利用GBDT分类方法,建立了模型预测误差分类模型,采用误差补偿的模型预测修正方法,得到经误差补偿后模型预测的断后伸长率有94.63%的样本数据绝对误差在±0.9%范围内,满足生产需求。