负载条件下RV减速器动态传动误差分析与试验

许立新 夏 晨 杨 博

1.重庆大学高端装备机械传动全国重点实验室,重庆,4000442.重庆大学机械与运载工程学院,重庆,400044

0 引言

RV减速器因其具备高精度、高刚性和小体积、大速比等优异传动性能,被广泛应用于工业机器人、精密机床等智能机械装备中。传动精度是RV减速器最重要的性能指标,也是RV减速器产品在出厂前必须检测并标识的关键性能参数。目前,RV减速器传动精度的测试与评价是在空载条件下进行的,无法反映减速器在负载情况下的真实传动精度性能。工程应用表明,随着工作负载的施加,RV减速器传动误差将增大,远远超出产品出厂标称指标,因此,如何考虑负载作用,揭示关键传动件公差设计与RV减速器动态传动误差之间的映射规律,从而准确评估RV减速器传动精度性能,是目前亟须解决的一个非常重要的理论难题。

近年来,众多学者围绕RV减速器传动误差建模开展了大量的研究工作。YANG等[1]建立了考虑多曲柄轴过约束传动结构影响的RV减速器传动误差等价模型,模型中将关键传动件制造误差等效为杆长误差模型,该模型的准确性得到了试验验证。基于静力学理论,LI等[2]建立了考虑齿廓修形和输出柱销间隙影响的RV减速器摆线针齿传动齿廓接触分析(tooth contact analysis,TCA)模型,对摆线传动静态传动误差进行了分析。基于TCA分析模型,SHIH等[3]分析了齿廓修形和针齿销位置度加工误差对摆线传动精度和回差特性的影响。LIN等[4]针对摆线传动提出了一种新的运动误差分析方法,该方法采用蒙特卡罗模型对传动件公差设计进行优化,可以获得摆线减速器较高的传动精度。SUN等[5]提出了一种改进型TCA分析方法,并针对国产新型摆线减速器(China bearing reducer,CBR)进行了传动误差分析。考虑摆线齿轮制造误差的影响,LI等[6]分析了RV减速器摆线针轮传动特性,探讨了摆线针轮啮合接触状态与减速器传动误差之间的映射规律。针对RV减速器高精度装配问题,CHU等[7]提出了基于遗传算法的零部件精度选配设计方法并验证了该匹配方法的可行性和有效性。李兵等[8]采用作用线增量法,建立了RV减速器传动误差分析模型,研究了各个构件的原始误差对输出转角误差的影响规律,揭示了各个构件原始误差的传递过程。

上述研究主要基于运动学或静力学理论研究RV减速器传动误差特性。在RV减速器动力学建模以及动态传动误差研究方面,韩林山等[9]综合考虑各传动零件的加工误差、安装误差、配合间隙及齿轮啮合刚度、轴承刚度等因素影响,建立了RV减速器的动态传动精度计算模型,完成了RV减速器全局误差敏感性分析[10]。郑钰馨等[11]采用集中质量法建立了五自由度纯扭转RV减速器动力学模型,分析了传动系统在启动和稳定过程中各部件的动态响应曲线以及整机传动误差频谱图。REN等[12]建立了RV减速器多自由度非线性动力学模型,研究了不同修形间隙下减速器转角位移和转速随时间的变化规律。将多体动力学方法与有限元方法相结合,CAO等[13]提出了一种考虑刚柔耦合作用的RV减速器动力学分析方法,研究了几何误差与构件弹性变形之间的耦合效应对系统动态传动精度的影响。在前期研究中,笔者基于接触多体动力学理论,考虑多曲柄轴过约束传动结构影响,建立了RV减速器摆线针轮传动机构的参数化动力学模型,研究了摆线修形齿隙和滚针轴承间隙对传动系统动态响应的影响[14]。

考虑输出扭矩负载作用的RV减速器动态传动精度分析必须依据动力学方法。基于前期研究,笔者提出建立两曲柄轴标准型RV减速器接触多体系统整机动力学模型,模型考虑渐开线齿轮传动、摆线针轮传动以及多组转臂轴承和支承轴承动态子结构对传动精度的影响。此外,给出了RV减速器关键传动件如曲柄轴、摆线轮和针轮的几何形状误差与加工位置度误差表达方法。通过接触多体动力学分析,探讨了负载扭矩变化对RV减速器动态传动误差的影响规律。最后,通过试验对动力学模型的精度以及分析结果的准确性进行了验证。

1 RV减速器接触多体动力学建模

1.1 RV减速器整机动力学建模架构设计

RV减速器传动原理如图1a所示,以两曲柄轴标准型RV减速器为对象,在多体系统动力学理论框架下,建立其整机动力学模型架构如图1b所示。建模过程中完整地考虑了RV减速器第一级渐开线齿轮传动和第二级摆线针轮传动子结构,同时考虑了多组转臂轴承和支承轴承的影响。模型中,假设行星齿轮与所在曲柄轴为同一个运动构件,输出盘与压紧盘为同一个运动构件(又称为输出行星架)。传动系统中共包括六个运动刚体,分别是一个输入齿轮轴、两组行星齿轮与曲柄轴组件、两片摆线轮和一个输出盘与压紧盘组件。图1b中,ωp表示输入齿轮轴转速,ωg表示行星齿轮转速,ωo表示输出盘转速,Tload表示减速器负载扭矩。

(a)RV减速器传动原理 (b)RV减速器动力学建模图1 RV减速器传动原理及其动力学建模架构设计Fig.1 Transmission principle and dynamic modelling architecture design of RV reducer

传动系统广义坐标共18个,具体表示为

(1)

系统质量矩阵可以表示为

Μ=diag(mp,mp,Ip,mg,mg,Ig,mg,mg,Ig,mc,mc,Ic,mc,mc,Ic,mo,mo,Io)

(2)

式中,mp、Ip分别为输入齿轮轴的质量和转动惯量;mg、Ig分别为行星齿轮与曲柄轴组件的质量和转动惯量;mc、Ic分别为摆线轮的质量和转动惯量;mo、Io分别为输出盘与压紧盘组件的质量和转动惯量。

系统约束方程可以表示为

(3)

式中,t为时间。

上述约束方程的作用在于保证减速器的输入齿轮轴和输出行星架仅保留回转自由度,同时约束输入齿轮轴以ωp匀速转动。系统中其他各传动构件的运动特性将由构件彼此之间的动态接触特性决定。

传动系统的动力学方程可以表示为

(4)

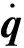
1.2 第一级渐开线齿轮传动部分接触建模

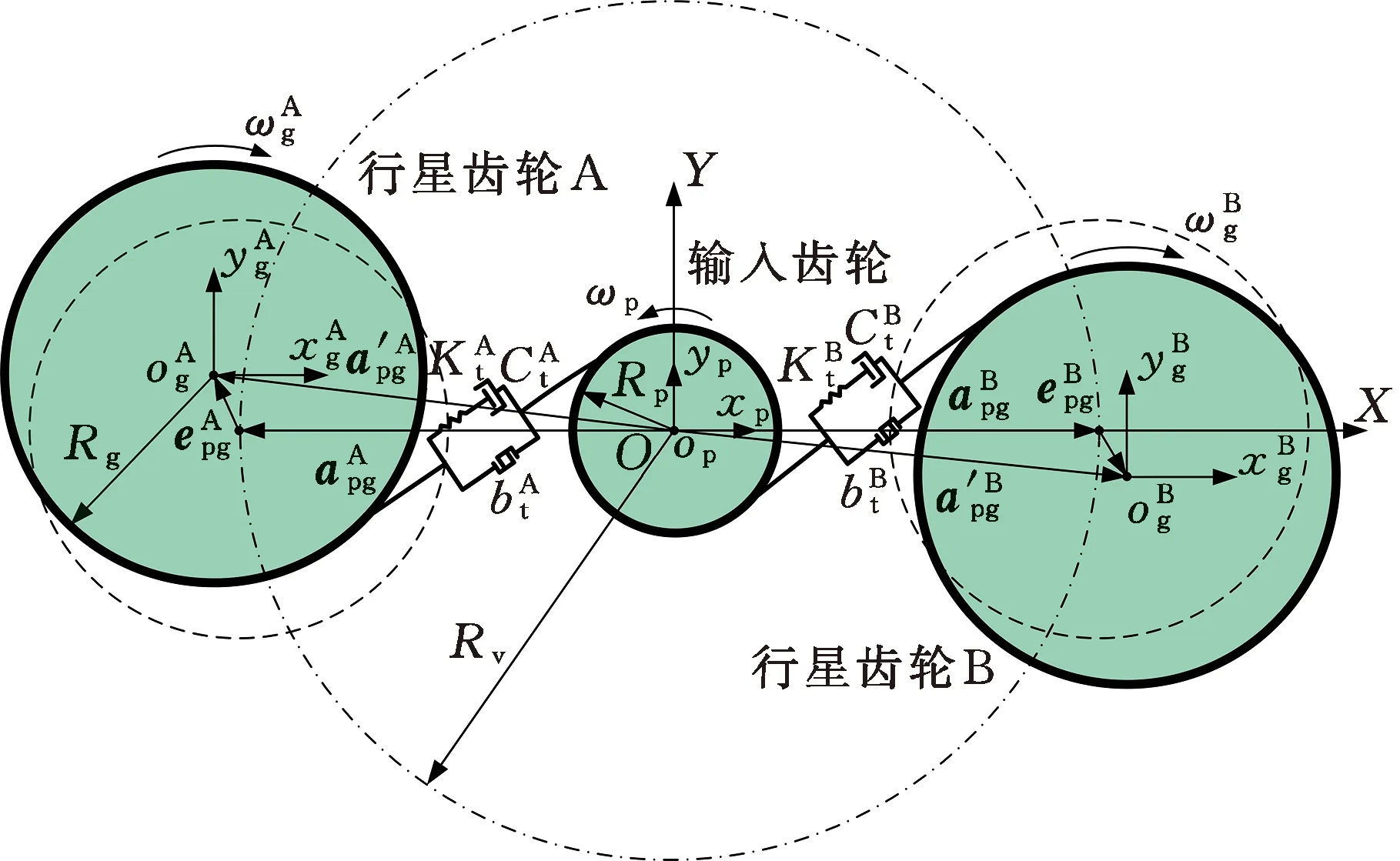
图2 RV减速器渐开线齿轮传动建模Fig.2 Involute gear transmission modeling of RV reducer

(5)

式中,R′A,BP为与行星轮A和行星轮B分别啮合时的主动轮节圆半径;Zp为主动轮齿数;s′A,Bp、s′A,Bg分别为主从动齿轮的节圆齿厚;bo为初始齿侧间隙;α′A,B为啮合角。

啮合角与实际中心距之间的函数关系可表示为

(6)

式中,a为齿轮理想中心距;a′A,B为行星轮A和行星轮B实际中心距;α为标准压力角。

由式(5)和式(6)可得齿轮副动态齿侧间隙表达式为

(7)

式中,inv(·)为渐开线函数。

齿轮啮合线方向上的相对位移可表示为

(8)

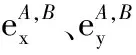
(9)

(10)

式中,km为平均啮合刚度;ka为时变啮合刚度幅值;ωm为齿轮啮合频率;φA,B为变刚度初始相位角。

(11)

式中,Cm为啮合阻尼给定值;d0、d1为接触深度临界值,d1>d0。

齿轮副动态接触啮合力可采用下式计算[15]:

(12)

1.3 第二级摆线针轮传动部分接触建模

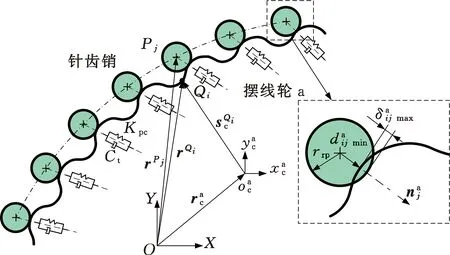
图3 摆线针轮接触分析模型Fig.3 Contact analysis model of cycloidal pinwheel

(13)

摆线轮齿廓与各个针齿销中心之间的相对位置矢量可以表示为

(14)

式中,j为针齿销序号。

在动力学计算中,将式(14)执行i×j次循环计算,即可完成某一瞬时下摆线轮与针轮之间的接触分析。

摆线齿廓与各个针齿销是否形成接触的判定条件为

(15)

式中,rrp为针齿销半径。

形成接触后,弹性接触变形可以采用下式计算:

(16)

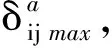
对应各个针齿销,接触线方向单位法矢量可以表示为

(17)

在接触线作用方向,摆线齿廓与针齿销相对法向速度可计算为

(18)

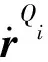
针齿销与摆线齿廓之间的接触力可以采用下式计算[14]:

(19)

式中,Kpc为摆线针齿销接触刚度;Cpc为摆线针齿销接触阻尼;cc为阻尼调节系数。

受摆线齿廓曲率半径变化影响,针齿销与摆线齿廓接触位置不同,接触刚度大小会有所不同。为简化计算,模型中将摆线针齿销接触刚度设为常数,其值由摆线平均曲率半径基于Hertz接触公式计算得到。

此外,阻尼调节系数的主要作用是保证接触分析过程的稳定性,其表达式如下:

(20)

式中,δ0、δ1为接触深度临界值,δ1>δ0。

1.4 转臂轴承与支承轴承部分接触建模

RV减速器中转臂轴承为滚针轴承,支承轴承为圆锥滚子轴承。由于所采用的非标准圆锥滚子轴承接触角较小,因此建模中仅考虑圆锥滚子轴承的径向支承作用,同时将圆锥滚子轴承的轴向预紧量根据接触角大小转化为径向预紧量。以摆线轮a中的一组转臂轴承和支承轴承为例,转臂轴承接触建模如图4所示,支承轴承接触建模如图5所示。

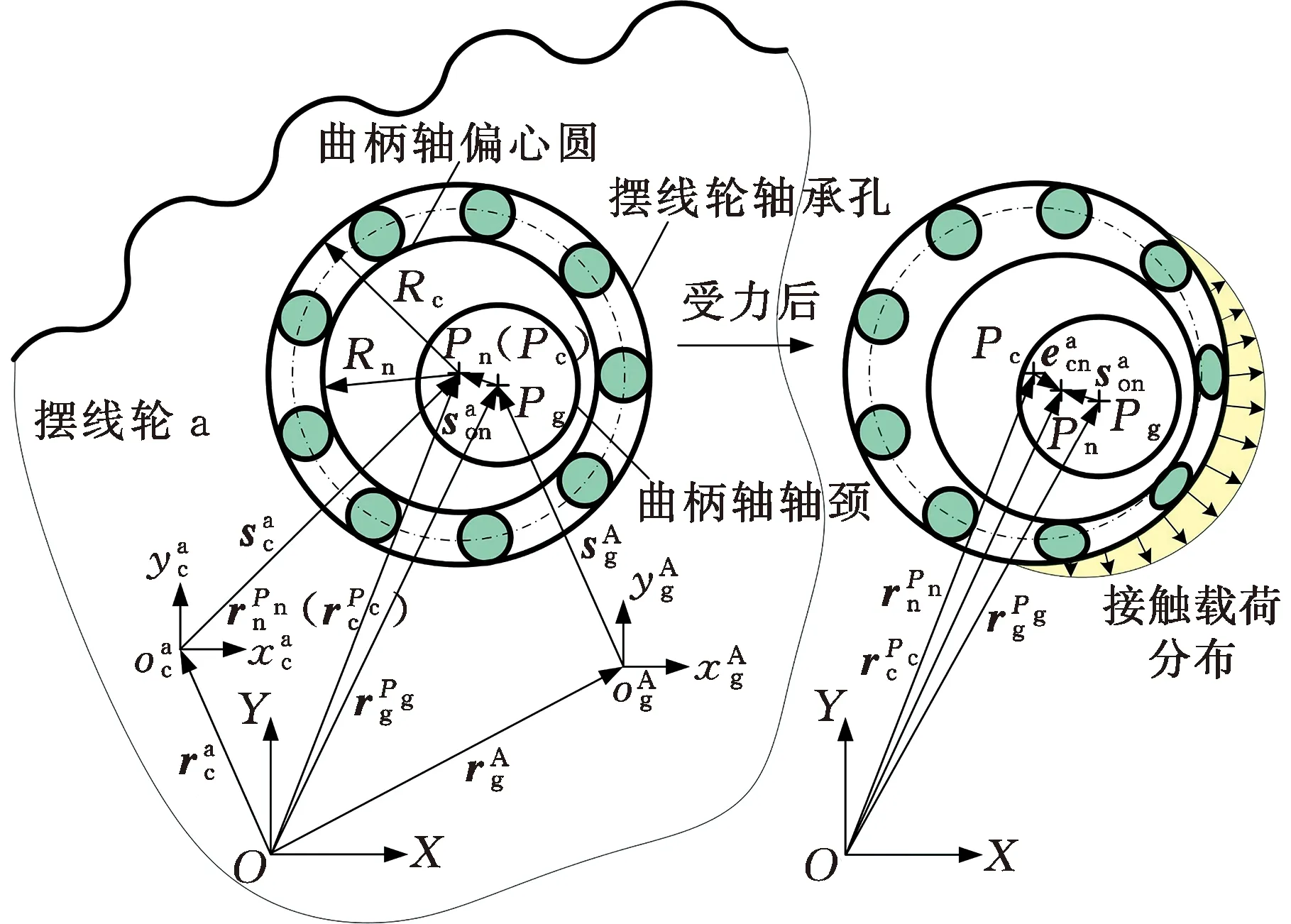
图4 转臂轴承接触建模Fig.4 Arm bearing contact modeling

图5 支承轴承接触建模Fig.5 Supporting bearing contact modeling

针对转臂轴承接触建模,首先将曲柄轴偏心外圆柱面和摆线轮轴承孔内圆柱面视为轴承滚动体内外滚道。在广义坐标系OXY下,轴承内外滚道几何中心Pc和Pn的位置矢量可以表示为

(21)

(22)

(23)

受间隙与弹性变形的影响,转臂轴承受力后内外滚道几何中心之间的相对偏心矢量可表示为

(24)

式(24)对时间求导,可得相对偏心速度矢量

(25)

轴承偏心距离可采用下式计算:

(26)

假设各滚动体在轴承套圈内均匀分布且同步转动,则滚动体公转角速度可采用下式计算:

(27)

式中,Rn、Rc分别为转臂轴承内外滚道半径;ωin、ωout分别为轴承内外滚道角速度,由曲柄轴和摆线轮角速度决定。

在轴承回转过程中,各个滚动体的转角位置可确定为

(28)

轴承内部各个滚动体在不同位置处的径向偏移可以采用下式计算

(29)

各滚动体在其相位方向上的相对偏心速度可以表示为

(30)

在不考虑径向游隙条件下,轴承各滚动体与滚道之间的法向接触力可以表示为[14]

(31)

式中,Kb、Cb分别为滚动体与滚道之间的接触总刚度和阻尼。

支承轴承的接触建模过程与上述转臂轴承类似,不同之处在于支承轴承需要考虑预紧作用。如图5所示,在广义坐标系下,支承轴承内外滚道几何中心Pg和Po的位置矢量可以表示为

(32)

(33)

式中,ro为输出盘与压紧盘组件局部坐标系原点在广义坐标系下的位置矢量;so为支承轴承外滚道几何中心在输出盘与压紧盘组件局部坐标系下的位置矢量;Ao为坐标转换矩阵,用于描述输出盘与压紧盘组件局部坐标系在广义坐标系下的方位。

支承轴承内外滚道几何中心之间的相对偏心矢量可表示为

(34)

轴承内部各个滚动体在不同位置处的径向偏移可以采用下式计算

(35)

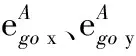
考虑轴承预紧影响,在式(31)基础上,支承轴承各滚动体与滚道之间的法向接触力可以表示为

(36)

2 关键传动件误差建模

根据工程制造经验,曲柄轴、摆线轮和针轮的加工制造精度是影响RV减速器传动精度性能的关键,因此,建模中将考虑上述关键传动件主要几何形状与位置度误差影响。

2.1 曲柄轴形位误差表达方法

图6 曲柄轴形位误差建模Fig.6 Crank shaft position error modeling

(37)

理想情况下,曲柄轴两个偏心圆的偏心距相等且相位角相差180°,考虑位置度误差后,偏心距大小及相位角可以采用下式确定:

(38)

(39)

2.2 摆线轮轴承孔形位误差表达方法

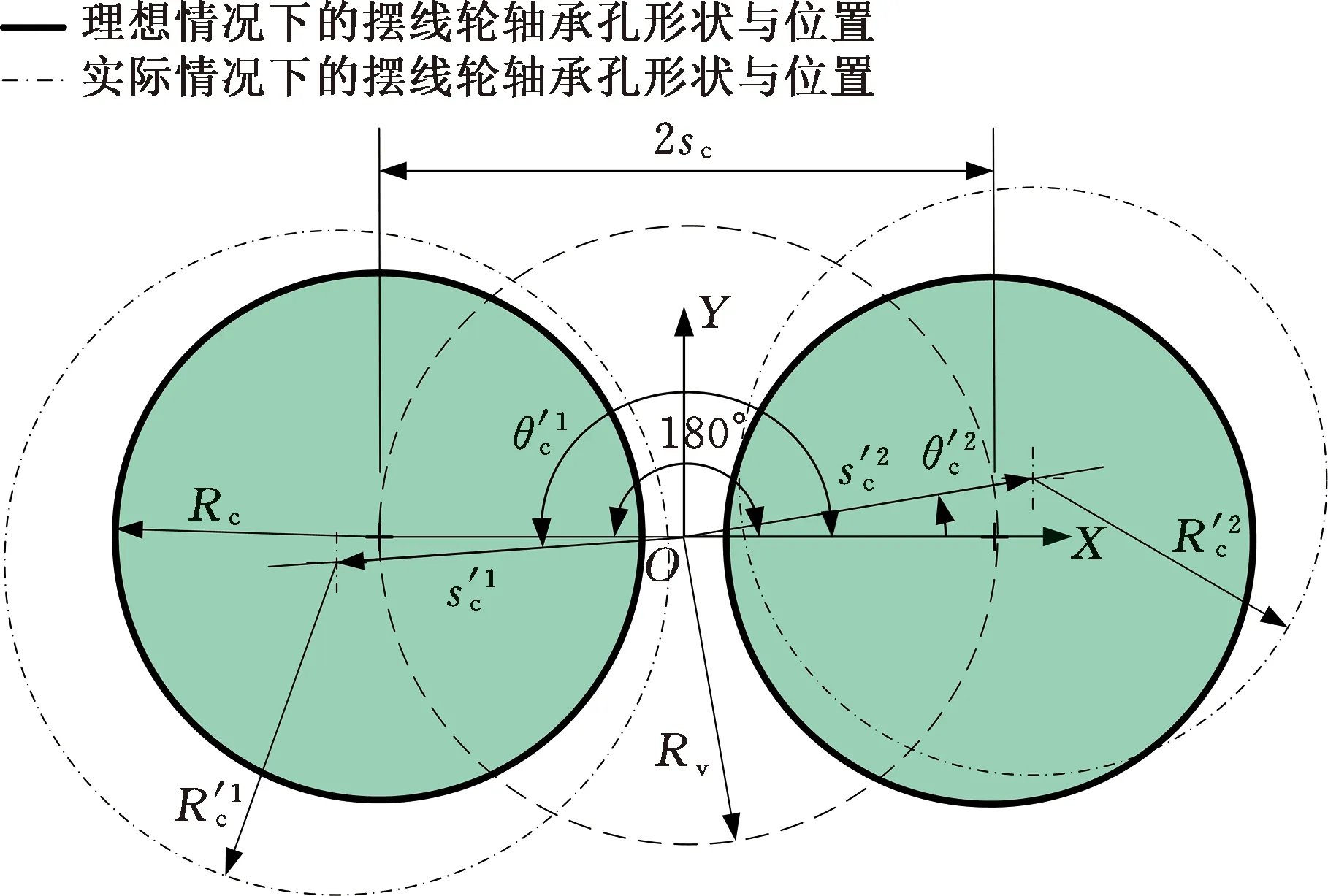
图7 摆线轮轴承孔形位误差建模Fig.7 Modeling of bore position error of cycloidal wheel bearings

(40)

理想情况下,摆线轮两个轴承孔分布圆半径相等且相位角相差180°,考虑位置度误差后,分布圆半径大小及相位角可以采用下式确定:

(41)

(42)

摆线齿廓也存在加工误差,这种齿形误差难以精确表达。此外,在工程设计中,也需要摆线齿与针齿销之间形成合理的齿侧间隙,以便于装配与润滑。考虑到这些影响,摆线轮将采用正等距修形方法进行修形,从而对齿形误差与齿侧间隙进行简化模拟。

2.3 针轮形位误差表达方法

针轮形位误差将考虑各个针齿销半径误差和针齿销位置度误差,如图8所示。理想情况下各个针齿销半径相同为rrb,计入加工随机误差后,各个针齿销实际半径将不同。采用随机函数表达各个针齿销实际半径大小为

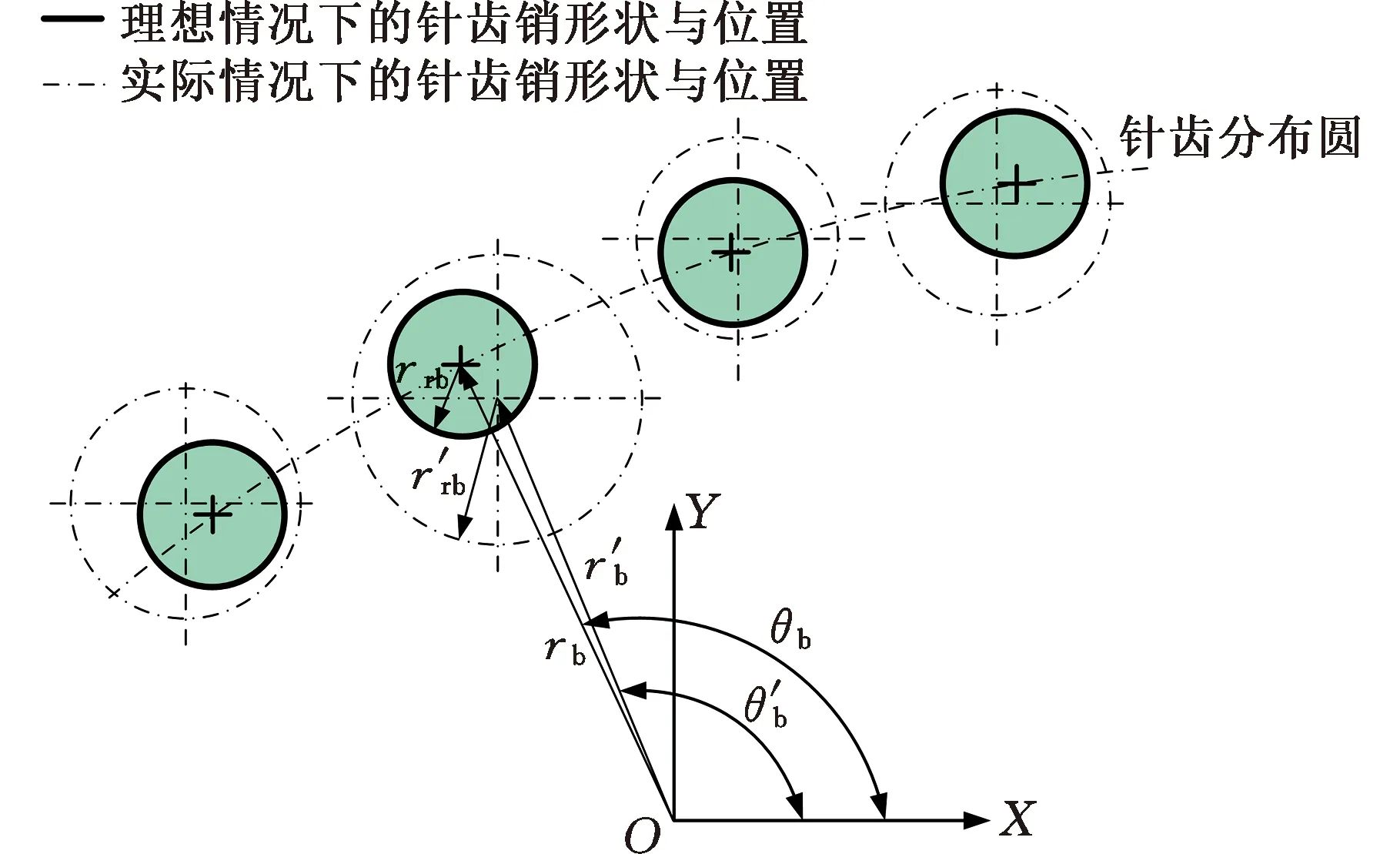
图8 针轮形位误差建模Fig.8 Pinwheel shape error modeling

(43)

理想情况下各个针齿销位于同一个分布圆上,分布圆半径为rb,计入加工随机误差后,各个针齿销分布径向距离将不同。采用随机函数表达各个针齿销位置误差:

(44)

(45)

3 算例分析、讨论与验证

3.1 RV20E模型参数

以工业机器人两曲柄轴标准型RV20E减速器(图1)为分析对象,该减速器传动比为121,其几何结构设计参数如表1所示,传动构件质量惯性参数如表2所示,关键传动件公差设计参数如表3所示,动力学分析参数如表4所示。此外,设定渐开线齿轮初始齿侧间隙为2 μm,摆线等距修形量为2 μm。

表1 零部件几何结构设计参数

表2 传动构件质量惯性参数

表3 传动构件公差设计参数

表4 动力学计算参数

3.2 动态传动误差计算

通过动力学计算,可以得到减速器输入端和输出端转角θp和θo的变化规律,结合减速器传动比ireducer,计算减速器传动误差:

ε=θp/ireducer-θo

(46)

通过修改负载扭矩Tload的取值大小,能够得到不同扭矩负载条件下的减速器动态传动误差变化规律。

图9和图10分别给出了空载条件下减速器动态传动误差时域与频域响应曲线。可以发现,在空载情况下减速器最大传动误差为57.5″,误差曲线周期性波动非常明显,在频率比为40附近,误差幅值贡献量最大。传动误差的频率用f表示,fo表示输出法兰盘的旋转频率,频率比f/fo代表了输出法兰每转一圈的传动误差变化量。图11和图12分别给出了在额定负载扭矩(167 N·m)条件下减速器动态传动误差时域与频域响应曲线,此时,传动误差最大值达到99.52″。显然,考虑额定负载作用后,减速器传动误差显著增大,相比于空载情况,额定情况下的最大传动误差增幅为73.1%。进一步分析,在空载情况下,减速器传动件之间的接触力可以忽略不计,因此导致传动误差的因素只能是因公差配合和摆线修形引入的传动界面间隙。而在负载情况下,除了受上述因素影响外,零件传力界面之间的弹性变形量将不能忽视。此外,由于渐开线齿轮传动部分位于减速器高速级,它对减速器输出误差影响非常有限,且分析中未考虑齿轮齿形几何误差的影响,因此在频域分析中观察不到齿轮传动对减速器输出误差的影响。

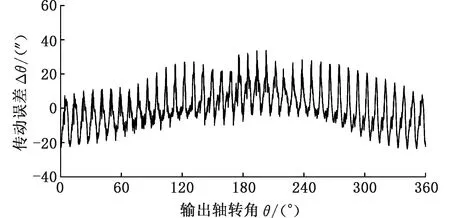
图9 空载条件下传动误差时域分析Fig.9 Time domain analysis of transmission error under no-load conditions

图10 空载条件下传动误差频域分析Fig.10 Frequency domain analysis of transmission error under no-load conditions

图11 额定负载条件下传动误差时域分析Fig.11 Time domain analysis of transmission error under rated load conditions

图12 额定负载条件下传动误差频域分析Fig.12 Frequency domain analysis of transmission error under rated load conditions

受机器人运动工况影响,RV减速器经常工作在变负载情况下,为探明负载变化对减速器传动误差幅值的影响,对不同负载作用下的减速器最大传动误差值进行了统计,如图13所示。在0.2To(To为额定扭矩)条件下,减速器传动误差幅值为72.09″;在0.4To条件下,减速器传动误差幅值为82.59″;在0.6To条件下,减速器传动误差幅值为88.99″;在0.8To条件下,减速器传动误差幅值为95.42″。总体表现出,随着负载扭矩的不断增大,减速器传动误差幅值随之增大,但幅值增长率却在下降。导致这一现象的主要原因在于,随着负载的增大,减速器传动零件接触界面之间的弹性接触变形随之增大,从而引起传动误差的逐渐增大。随着负载扭矩的增大,传动零件之间将逐渐克服配合间隙,传动零件之间的有效接触点逐渐增多,减速器整机扭转刚度逐渐增大,因此随着扭矩的线性增大,接触弹性变形量并非线性增大,导致减速器传动误差幅值增长率逐渐降低。

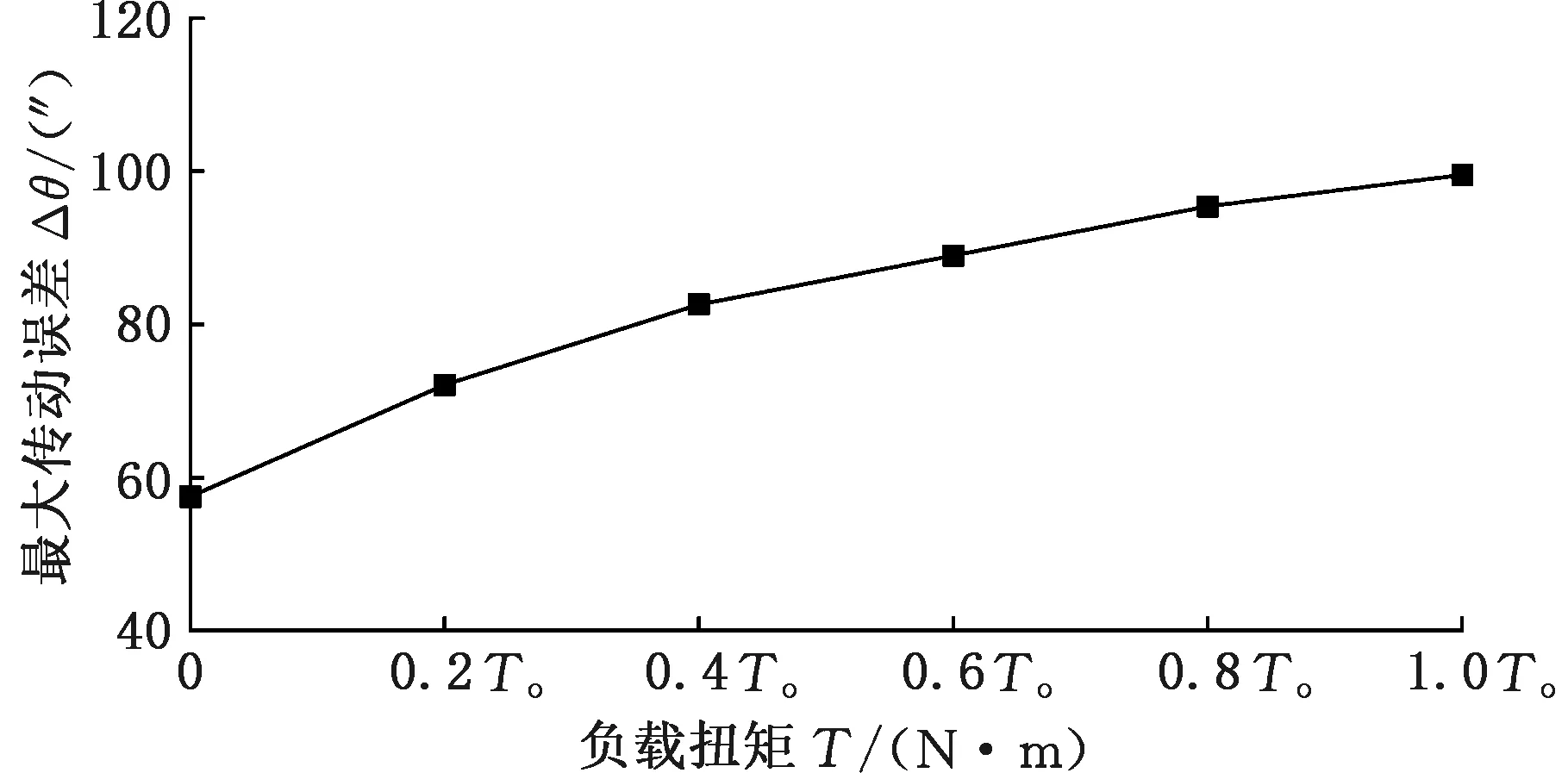
图13 不同负载扭矩条件下传动误差幅值变化Fig.13 Change of transmission error amplitude under different load torque conditions

3.3 动态传动误差试验

RV减速器传动精度测试试验台如图14所示,包括驱动装置、被测RV减速器、测量装置及加载装置。驱动电机为减速器提供动力,中间是被测试RV20E减速器,测量装置主要包括输入端与输出端的角度编码器以及数据采集设备,采用力矩电机作为加载装置,各部分之间用联轴器连接。该测试试验台的主要性能参数详见表5。

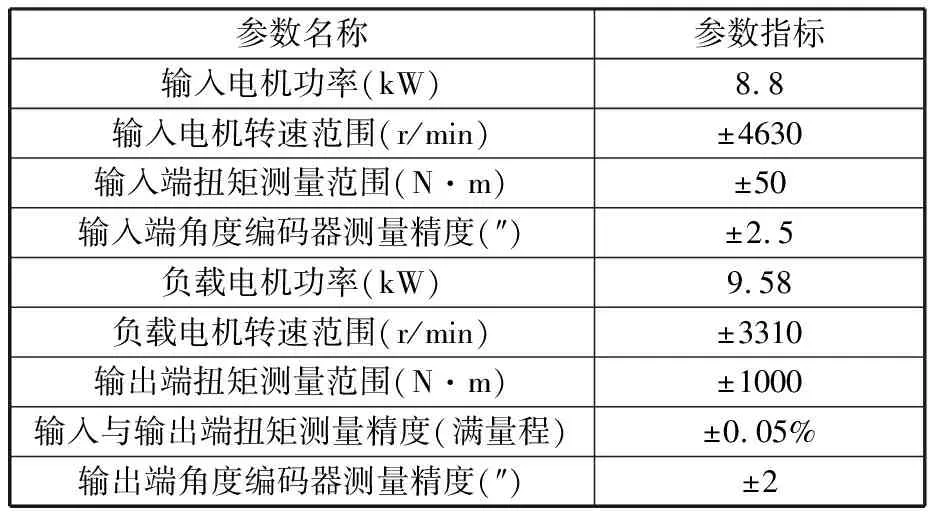
表5 试验台参数

图14 RV减速器传动精度测试试验台Fig.14 RV reducer transmission accuracy test bench

图15和图16分别给出了空载条件下减速器动态传动误差测试曲线及其频域分析结果。测试结果表明,该减速器空载条件下最大传动误差为69.34″,同样在频率比40附近,误差幅值贡献量最大。图17和图18分别给出了加载额定扭矩后减速器动态传动误差测试曲线及其频域分析结果。此时,传动误差最大值达到110.25″,相比于空载情况,最大传动误差增幅为58.9%。此外,加载额定扭矩后,传动误差在频率比80附近误差幅值贡献量最大。需要指出的是,减速器传动误差测试结果将不可避免地受试验台本身装配精度、检测精度和系统刚性的影响,因此误差幅值将比理论分析值略大,但基于时域与频域测试结果所反映出的传动误差变化特性与理论计算结果具有很好的一致性,足以验证理论模型的有效性。

图15 空载条件下传动误差时域测试结果Fig.15 Time domain test results of transmission error under no-load conditions

图16 空载条件下传动误差频域分析结果Fig.16 Transmission error frequency domain analysis results under no-load conditions

图17 额定扭矩条件下传动误差时域测试结果Fig.17 Time domain test results of transmission error under rated torque

图18 额定扭矩条件下传动误差频域分析结果Fig.18 Transmission error frequency domain analysis results under rated torque

4 结论

(1)针对扭矩负载作用下RV减速器动态传动误差分析问题,考虑关键传动件几何形状与位置度多源误差影响,建立了两曲柄轴标准型RV减速器动力学模型,模型中考虑了渐开线齿轮传动、摆线针轮传动以及多组转臂轴承和支承轴承动态子结构的影响,深入探讨了扭矩负载作用下减速器动态传动误差特性。

(2)基于理论模型得到空载情况下减速器最大传动误差为57.5″,额定扭矩情况下最大传动误差达到99.52″,传动误差增幅为73.1%。随着负载扭矩的不断增大,减速器传动误差幅值随之增大,但幅值增长率却在逐渐下降。

(3)基于试验测试得到空载情况下减速器最大传动误差为69.34″,额定扭矩下最大传动误差达到110.25″,传动误差增幅为58.9%。基于时域与频域测试结果所反映出的传动误差变化特性与理论计算结果具有很好的一致性。