行星轮齿轮箱太阳轮齿根裂纹传递特性分析

沈子钰 张 砦 王友仁 李泓锟

南京航空航天大学自动化学院,南京,211106

0 引言

行星齿轮箱能在有限的狭窄空间内完成大传动比的输出,具有体积小、传动平稳、效率高以及传递功率大等优点。凭借紧凑性和高功率传动比的独特优势,行星齿轮箱广泛应用于航空航天、汽车、重型卡车和地下煤矿设备等。然而,由于工作环境恶劣,齿轮箱极易产生点蚀、裂纹等故障,导致性能下降,甚至引发重大事故,因此对行星齿轮箱进行故障诊断研究对避免安全事故的发生具有重要意义。

相比定轴齿轮箱,行星齿轮箱传动过程具有振动传递路径时变效应[1]。行星齿轮箱内的啮合振动需要经过复杂路径传到箱体表面才能被传感器获取,因此,振动传递机理是行星轮齿轮箱故障诊断研究的重要内容。

国内外学者关于行星齿轮箱振动传递机理的研究主要是针对齿轮啮合振动信号和齿轮箱箱体表面信号进行的。针对齿轮啮合振动信号,主要是建立多种动力学模型。易钰棠[2]建立了包含传动系统平移-扭转的54自由度集中参数模型,对齿轮传动内部激励、动态啮合力进行了计算,对齿轮箱振动响应进行了预估;王箫剑等[3]提出了考虑太阳轮制造误差的修正等效啮合尺寸模型, 该方法能够准确找到系统的各特征频率,且各频率分布与真实情况较为接近;SHEN等[4]基于集中参数建模方法,建立了纯扭转动力学模型,分析了故障对系统振动响应的影响;于欣楠等[5]建立了共振频带内齿轮故障振动信号的调幅-调频模型,得出了故障振动信号时变边带的瞬时频率关于共振频率对称分布的结论。

针对箱体表面振动信号,主要是建立不同传递路径函数。张建宇等[6]通过模态叠加法完成了单级齿轮箱的冲击响应分析;WANG等[7]通过对传动特性的分析,揭示了行星齿轮磨损故障和多级齿轮啮合之间的关系;马浩群等[8]在行星轮载荷分布不均的故障下,通过高斯窗描述时变传递路径;GAO等[9]建立了齿轮系统的三维实体刚柔耦合模型,采用系统辨识的方法建立了各路径对应的传递函数模型,通过传输特性分析揭示了信号传输过程。

上述文献对振动传递机理已经进行了深入的研究,但仍有一些不足值得讨论:在传递路径方面,只是简单采用汉宁窗进行表示,但是汉宁窗仅描述了靠近传感器的齿圈圆周与行星轮啮合所产生的振动信号,对其他圆周上的啮合振动信号置零[10];只是考虑时变路径而没有考虑时不变路径,对边频带调幅调频规律的研究还不够。

针对以上不足,本文综合考虑行星齿轮箱内外啮合的时变和时不变6条传递路径,给出改进高斯窗的时变路径函数和考虑齿轮箱材料的时不变路径函数,建立正常情况和太阳轮裂纹故障下的箱体表面振动信号模型,对比正常情况与裂纹故障下内外啮合振动信号的边频带差异,探究调制边频带成分变化规律。并搭建行星齿轮箱试验台,与模型响应信号频谱进行对比分析,以验证振动信号模型的准确性。

1 行星齿轮箱啮合振动模型

采用弯曲-扭转耦合集中参数模型[11]分析齿轮副啮合振动的信号特征,通过求解运动微分方程的方法区分不同啮合振动的频率来源。

本文研究对象为单级行星齿轮箱,行星轮中行星架的运动微分方程为

(1)

内齿圈的运动微分方程为

(2)

太阳轮的微分方程为

(3)

第n个行星轮的运动微分方程为

(4)

式中,n为行星轮个数;mq、Iq、rq、kq(q=s,p,r,c)分别为太阳轮、行星架 、内齿圈、行星轮的质量、转动惯量、基圆半径和支撑刚度;xi、yi(i=s,c,r,1,2,…,n)分别为系统振动使构件i的质心偏离理论位置的线位移;ui为振动产生角位移折算到圆周上的线位移;ksn、krn分别为外啮合和内啮合的时变啮合刚度;Tc、Ts分别为行星架和太阳轮的输入扭矩;ψrn、ψsn为内齿圈与太阳轮上啮合点相对于中心坐标系的角度;δcnx、δcny、δcnu分别为行星架与行星轮在x方向、y方向和行星架切向的相对位移;δsn为内啮合在啮合线方向的相对位移;δrn为外啮合在啮合线方向的相对位移;ωc为行星轮角速度。

将行星轮系各部件间的相对位置关系代入上述构件的微分方程中,整理得到矩阵形式的行星齿轮箱的总微分方程如下:

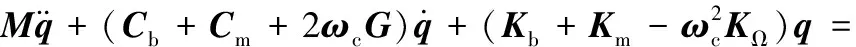
(5)

式中,M为系统质量矩阵;Cb、Cm分别为系统支承阻尼矩阵和啮合阻尼矩阵;G为陀螺矩阵;Kb、Km分别为系统的支承刚度矩阵和啮合刚度矩阵;KΩ为向心刚度矩阵;T为外激励矩阵;E为系统误差激励矩阵;q为系统广义坐标列阵。

2 行星齿轮箱箱体表面振动信号模型

2.1 传递路径影响分析

在实际应用中,传感器通常安装在齿轮箱外壳上,以获取整个齿轮箱的振动信号。文献[12-15]总结了行星轮齿轮箱内外啮合的主要传递路径,如图1所示。6条路径分别为:① 行星轮→内齿圈→箱体→传感器;②行星轮→行星轮中心轴→行星架→箱体→传感器;③行星轮→太阳轮→太阳轮中心轴→箱体→传感器;④太阳轮→行星轮→行星轮中心轴→行星架→箱体→传感器;⑤太阳轮→行星轮→内齿圈→箱体→传感器;⑥太阳轮→太阳轮中心轴→箱体→传感器。6条路径中,路径1和路径5由于啮合点与传感器之间的距离具有周期性,为时变传递路径;路径2、3、4、6由于啮合点与传感器之间的距离固定,为时不变传递路径。

图1 行星齿轮箱振动传递路径示意图Fig.1 Planetary wheel vibration transmission path diagram

在以往的研究中,时变传递路径多采用汉明窗或汉宁窗表示,只考虑传感器附近的齿轮圆弧部分与行星齿轮之间的啮合振动,模拟的传递路径误差大[16]。在考虑箱体尺寸和材料传递特性等因素时,时不变路径的影响不可忽视。为了解决上述问题,本文提出了改进的时不变和时变路径函数。

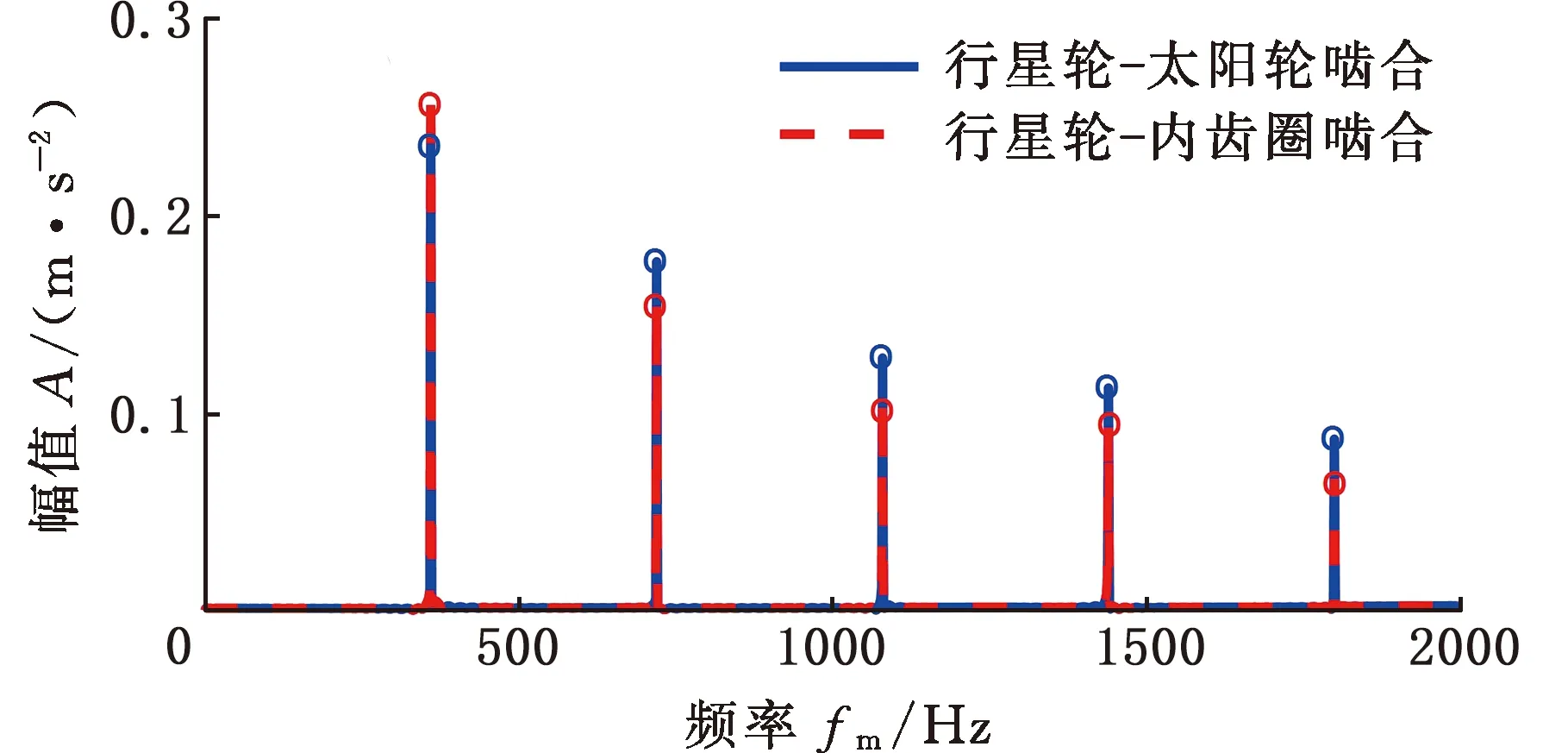
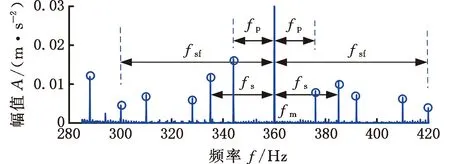
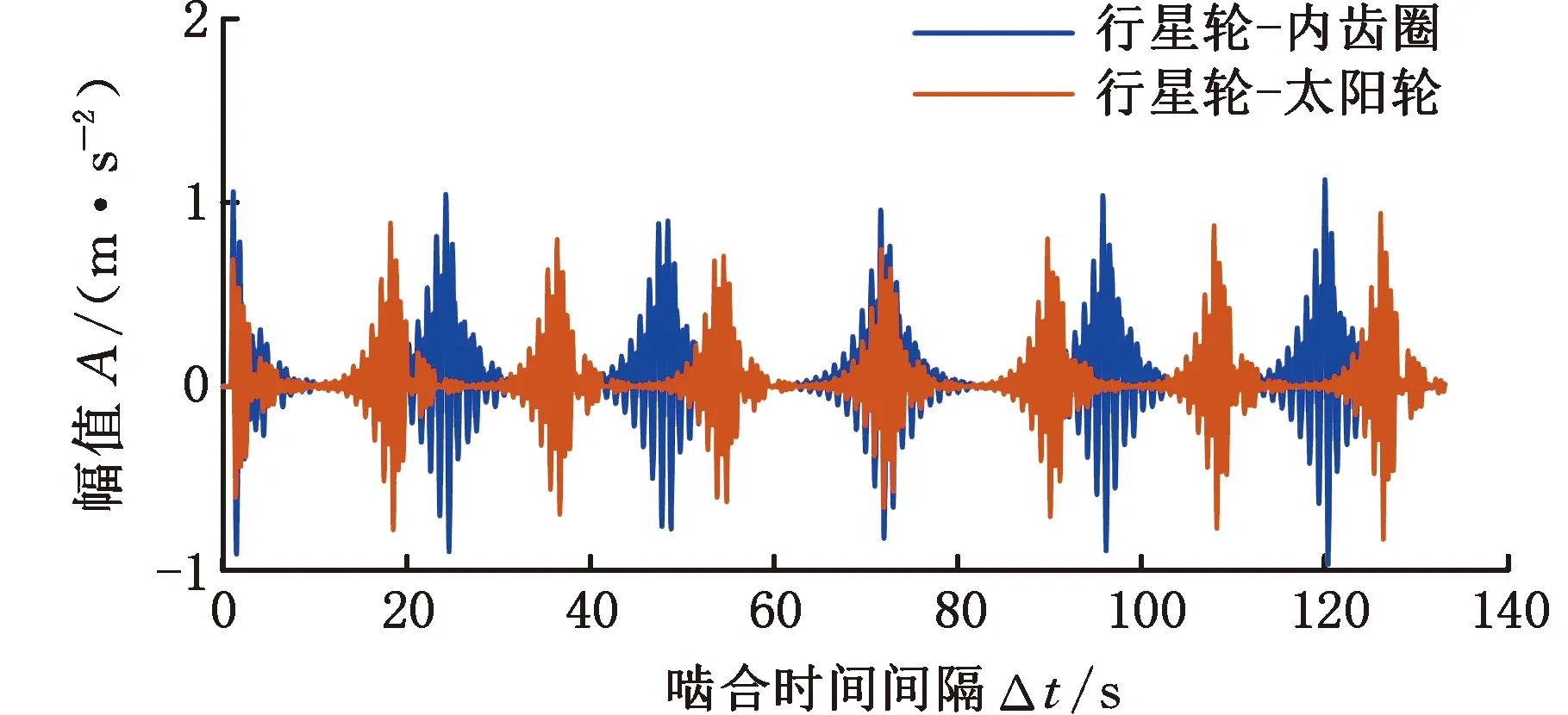
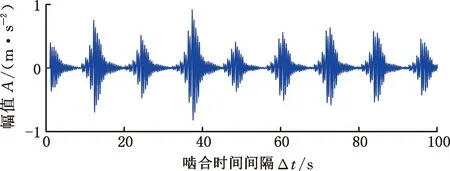
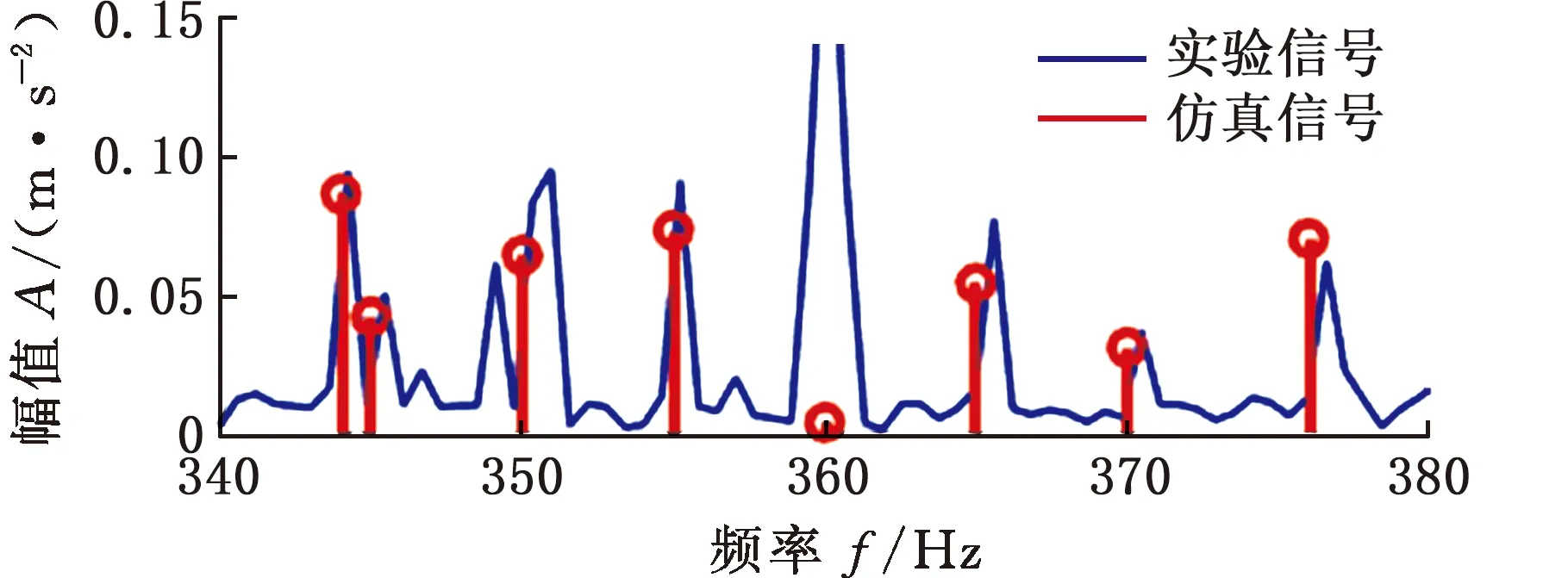
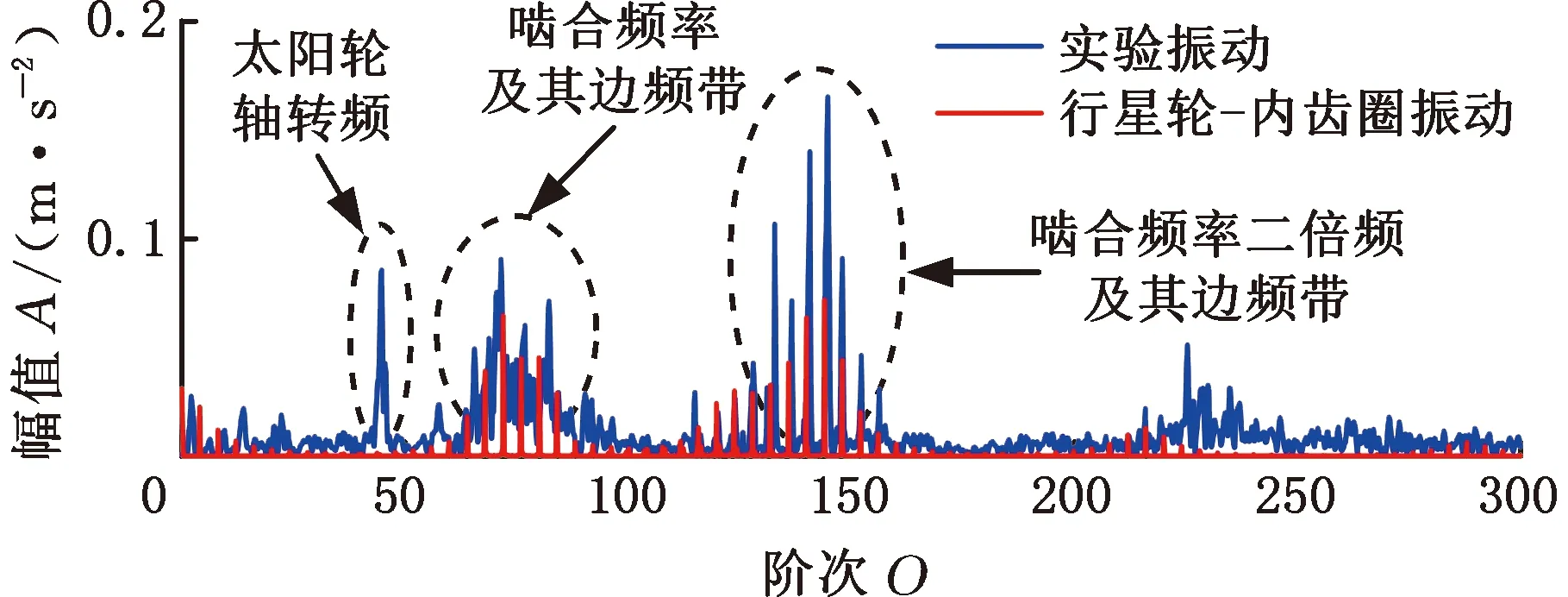
对于时不变传递路径,路径长度(从啮合点到传感器)是恒定的,导致振动能量幅值恒定衰减。对于内齿圈、行星轮和太阳轮,时不变传递路径分别表示为Cr、Cp和Cs。由于传感器直接固定在外壳上,Cr值的选择由箱体材料阻尼系数决定,太阳轮的振动在到达壳体时会出现衰减,因此Cs值随着不同传递路径引起的不同衰减水平而变化,其选择由齿轮、轴承和箱体的材料阻尼系数决定;行星轮振动包含两个啮合点——太阳轮-行星轮振动和内齿圈-行星轮振动,因此行星轮振动可以认为是上述两个独立部分的总和,即Cp=aCr+bCs,其中,a、b为权重,0

对于时变传递路径,根据振动能量的传播理论,振动衰减归因于材料阻尼,并与距离成指数关系[17]。当振动沿传输路径传输时,受传输路径影响的能量损失[18]可表示为w(t)=w0exp(-t),因此,与汉宁窗相比较,通过高斯窗表示时变传递路径更符合振动能量传播理论。

然而通过传统的高斯窗模拟传递路径效应,当行星轮位于距离传感器最远的位置时,影响为零。但在齿轮箱实际工作中,啮合振动信号会通过整个齿圈圆周传递至传感器,为了克服这一缺点,本文在传统高斯窗的基础上进行了改进。改进后的高斯窗函数为

wi(t)=α-(1-α)Fexp(-lri(t)ζ/h)

(6)

其中,α用于控制窗口函数的最小值和带宽,0.5≤α<1;F为强度因子;h为衰减因子;-lri(t)为时变路径长度。随着α的增大,窗函数具有更大的最小值和更宽的带宽,可以获取更多的振动信号,同时考虑箱体尺寸因素,引入几何参数因子ζ=2m-1,m为模数[19]。

2.2 正常情况时的振动信号模型

箱体表面传感器接收的振动信号可以视为行星轮齿轮箱不同振动源的加权和。本文主要考虑齿轮在传递路径影响下的啮合振动,模型建立思路如图2所示,具体表达式为

图2 模型建立流程图Fig.2 Modeling flow chart

(7)

(8)

式中,*是卷积运算;Ln为载荷分布比;u(t)为齿轮箱系统的固有振动;β为结构阻尼系数;fn为固有频率;y(t)整体可以视为啮合振动的冲击函数与正弦衰减固有振动函数的卷积;Cp、wrpn(t)分别为时不变传递路径和时变传递路径分别对内齿圈-行星轮振动的影响;Cs、wspn(t)分别为时不变传递路径和时变传递路径分别对太阳轮-行星轮振动的影响;vrpn为内齿圈和第n个行星轮的振动;vspn为太阳轮和第n个行星轮的振动。

将齿轮的啮合振动通过Dirac脉冲函数表示为

(9)

其中,δ(t)代表单个脉冲。通过计算得到啮合频率fm=zrfc=zs(fs-fc),其中,zs为太阳轮齿数,fs为太阳轮转频,fc为行星架转频。最终内齿圈-行星轮啮合振动可以表示为

(10)

式中,Arpi为第i个行星轮-内齿圈啮合振动的幅值;φi为每个行星轮偏离标称位置时的误差;θi为第i个行星轮与内齿圈啮合的相位差。

同样,行星轮-太阳轮啮合振动表示为

(11)

式中,Aspi为第i个行星轮-太阳轮啮合振动的幅值;φi为第i个行星轮与太阳轮啮合的相位差。

2.3 太阳轮齿根出现裂纹时的振动信号模型

当太阳轮齿根出现裂纹时,齿轮啮合振动的振幅与振频也会随之变化,从而产生谐波分量。引入调幅调频函数ak(t)、bk(t)表示第k次谐波分量[20],有

(12)

(13)

式中,fsf为太阳轮裂纹故障频率;Akg、Bkg分别为调幅和调频强度,Akg>0,Bkg>0;φkg为第k次谐波的第g阶角相位。

在太阳轮裂纹故障下的振动信号模型为

(14)

3 仿真分析

3.1 啮合振动信号特征

本小节根据集中参数模型得到外啮合和内啮合的振动频谱结构特征,进而分析啮合振动的信号特征。基本参数按照表1进行设置,行星轮齿轮箱各构件特征频率按照表2计算得到。

表1 行星轮齿轮箱动力学模型基本参数

表2 行星轮齿轮箱各构件特征频率

正常情况下的啮合点频率特征如图3所示。由图3可知,齿轮啮合振动的频率成分为啮合频率fm=360 Hz及其倍频,并且振幅呈现逐渐递减的趋势。在正常情况下,外啮合与内啮合的频率特征结构完全一致,仅在幅值上存在差别。

图3 正常情况下啮合点振动响应频率特征Fig.3 Vibration response frequency characteristics of the engagement point under normal conditions

太阳轮裂纹情况下的啮合振动频率特征如图4所示。裂纹损伤产生的冲击性信号在频域中表现为调幅调频现象。啮合频率及其倍频附近会产生不对称边频带。在外啮合的振动响应频谱中,边频带呈现集中分布的趋势,边频带位置可总结为:啮合频率fm及其倍频两侧产生以行星轮转频fp和行星架转频fc为间隔的多阶调制边频带,即jfm±jfp,jfm±jfc,其中,j为啮合频率倍频数。在内啮合的振动响应频谱中,边频带呈现全频域分布的趋势,边频带位置可总结为:啮合频率fm及其倍频两侧产生以太阳轮转频fs、行星轮转频fp和太阳轮故障频率fsf为间隔的多阶调制边频带,即jfm±jfs,jfm±jfs±jfp,jfm±jfsf。在故障情况下,啮合频率及其倍频振幅不再呈现递减的趋势,低频部分出现太阳轮转频fs和太阳轮故障频率fsf及其倍频的频率成分。

(a)外啮合振动响应频率特征

3.2 传递路径信号调制特征

3.2.1外啮合传递路径振动调制特征

外啮合的传递路径函数产生的振动响应频谱如图5所示,以啮合频率附近频带为例,其振动调制特征表现为行星架与行星轮转频及其倍频成分。路径1导致产生了上述规律的边频带特征,即起到了调幅调频的效果。但是在仅考虑路径1的情况下,边频带幅值较小,如图5a所示。在增加了路径2和路径3后,边频带幅值增大,如图5b所示,时不变路径起到调幅作用,能更好地表示微弱的振动信号。在太阳轮裂纹故障下,外啮合传递路径响应特征表现规律与正常情况下相同,仅幅值存在差异,这里以正常情况下为例。

(a)外啮合路径1频谱

3.2.2内啮合传递路径振动调制特征

正常情况下内啮合的传递路径函数产生的振动响应频谱如图6所示,路径5导致出现调幅调频现象,产生以行星轮与太阳轮转频及其倍频为主要成分的边频带。路径4、路径6导致出现调幅现象,使边频带幅值增大。

(a)内啮合路径5频谱

太阳轮裂纹故障下内啮合的传递路径函数的振动响应频谱如图7所示。与正常情况下相比,啮合频率的边频带除行星轮与太阳轮转频成分外,增加了太阳轮裂纹故障频率,同时裂纹故障也会影响边频带的幅值大小,与传递路径一起产生调幅现象。

(a)内啮合裂纹故障路径1频谱

通过以上分析可以得出:时变传递路径引起调幅调频现象,时不变传递路径引起调幅现象,在同时考虑时变和时不变路径时,边频带的振幅特征更加准确,有利于微弱故障信号的及时发现。太阳轮裂纹故障下仅在内啮合的频谱内出现故障频率。因此通过内外啮合的区分,可以确定行星齿轮箱局部故障的位置。

3.3 箱体表面振动信号特征

正常情况下,内外啮合振动到达箱体表面的振动信号时域和阶次谱如图8所示。由图8a可得,正常情况下内外啮合存在明显的周期性,1个公转周期对应3个等间隔包络,外啮合的时域振动周期较长且振幅较大,内啮合的时域振动周期较短且幅值较小。由图8b可得,以行星架转频为参考频率得到相应阶次谱,啮合频率对应阶次谱中第72阶。外啮合阶次谱振幅较大,因为路径1距离传感器最近,接收信号最强;同时,在啮合频率附近产生由行星轮公转和传递路径调制引起的振幅不对称边频带,行星轮公转阶次为3,对应{…,66,69,75,78,…}阶次。内啮合振幅相对较小,在啮合频率附近产生由太阳轮自转和传递路径调制引起的振幅不对称边频带,太阳轮自转阶次为5,对应{…,62,67,77,82,…}阶次。

(a)外啮合与内啮合时域

由于太阳轮裂纹为局部故障,对外啮合的影响仅会导致幅值大小的变化,因此主要关注太阳轮裂纹故障下内啮合振动到达传感器的振动响应信号。图9为太阳轮裂纹情况下内啮合到达箱体表面传感器的振动信号时域图。在故障情况下,一次行星架旋转周期内的冲击振幅不再具有一致性,并且啮合间隔相比于正常情况下更为短暂。

图9 太阳轮裂纹情况下内啮合时域谱Fig.9 Time domain spectrum of internal meshing in case of sun wheel cracks

图10为太阳轮裂纹情况下内啮合到达箱体表面传感器的振动信号阶次谱图。啮合频率阶次附近与正常情况下相比,出现由于裂纹故障引起的细小边频带。啮合频率二倍频对应阶次144阶附近边频带更为密集,其主要成分为:太阳轮转频对应阶次{…,129,134,139,149,154,159,…},太阳轮故障频率对应阶次{…,120,132,156,168,…}。

(a)啮合频谱附近

利用本文建立的模型分析了行星齿轮箱正常情况和太阳轮裂纹故障下,箱体表面的振动信号特征。在正常情况下,内外啮合均以啮合频率阶次及其倍频为载波,但是外啮合以行星轮公转频率为调制阶次,内啮合以太阳轮自转频率为调制阶次。调制现象是由齿轮啮合与传递路径的共同作用导致的。在太阳轮裂纹故障下,外啮合振动特征基本不变,内啮合振动特征出现以故障频率为调制阶次的边频带。对比内外啮合的信号特征可以分析出行星齿轮箱局部故障发生位置。

4 实验验证

为模拟行星齿轮箱实际工作条件,实验在HFXZ-I行星齿轮箱故障诊断试验平台上进行,试验平台与试验件如图11所示。试验平台的行星齿轮箱基本参数与表1和表2 的仿真参数设置相同,输入转速设定为1500 r/min,传感器采样频率设置为10 kHz,采集太阳轮正常和早期裂纹故障时的振动加速度信号。在正常情况和太阳轮1 mm齿根裂纹的故障下,将模型仿真内外啮合振动数据与实验数据进行比较。

图11 行星轮试验平台与试验件Fig.11 Planetary wheel test platform and test pieces

4.1 传递特性验证

在太阳轮裂纹情况下,将啮合频率附近内外啮合混合传递路径函数振动响应频谱与实验数据进行对比,结果如图12所示。通过与实验数据对比可知,本文改进后的高斯窗函数作为时变传递路径可以准确获得边频带位置,外啮合的调制位置为nfm±jfp±jfc,内啮合裂纹故障下调制位置为nfm±jfp±jfs±jfsf。在共同考虑时变和时不变路径后边频带幅值与实验信号振幅更加接近。

(a)外啮合边频特征对比

4.2 箱体表面振动信号验证

将本文模型与箱体表面传感器振动信号进行对比验证,正常情况下的对比结果如图13所示。正常情况下行星轮-内齿圈啮合的阶次特征主要集中在啮合频率阶次Om及其边频带附近,边频带位置为:Om±jOp(Op为行星轮转频对应阶次)。行星轮-太阳轮的阶次特征主要集中在啮合频率二倍频阶次2Om及其边频带附近,边频带位置为:2Om±jOs±jOp(Os为太阳轮转频对应阶次)。

(a)外啮合仿真与实验信号对比

图14所示为太阳轮裂纹下齿轮箱内外啮合与实验振动信号的对比结果。实验信号在50阶附近出现了太阳轮轴转频。外啮合阶次特征主要集中在啮合频率阶次Om及其边频带附近,内啮合阶次特征主要集中在啮合频率二倍频阶次2Om及其边频带附近。在太阳轮裂纹故障下,与太阳轮齿根裂纹故障相关的信息主要集中在啮合频率二倍频对应的阶次。啮合频率对应阶次处的振幅明显减小。外啮合的边频带位置对应规律不变,仍然为2Om±jOp。而内啮合啮合频率二倍频处的边频带位置规律发生变化,边频带更加密集,对应位置为:2Om±jOp±jOs,2Om±jOsf(Osf为太阳轮故障频率对应阶次)。

(a)外啮合仿真与实验信号对比

通过实验分析了行星齿轮箱传递路径引起的振动调制机理,综合考虑时变和时不变路径使得仿真信号与实验信号更为近似,同时利用本文所建立的模型可以分别得到外啮合与内啮合到达箱体表面的振动信号时域、频域特征,验证了正常情况和太阳轮齿根裂纹故障下的传递特性规律和频谱结构,通过分析内外啮合频率特征的差异有助于确定齿轮箱局部故障的位置。

本文模型可实现全频、定量模拟行星齿轮箱振动信号,能较好地反映箱体表面振动信号频率信息、幅值信息、边频带信息的特征,适用于正常工况与齿轮局部型故障。

5 结论

(1)改进了行星齿轮箱箱体表面振动信号数学模型,考虑行星轮-内齿圈(外啮合)、行星轮-太阳轮(内啮合)振动,改进时变传递路径和时不变传递路径函数,使模型更加切合实际信号。

(2)分析了正常和太阳轮齿根裂纹故障下行星齿轮箱啮合振动的信号特征。正常情况下齿轮箱啮合点处的频率成分为啮合频率及其倍频,并且振幅呈现逐渐递减的趋势。太阳轮齿根裂纹故障下,外啮合呈现集中于啮合频率及其倍频的边频带,位置为:jfm±jfp,jfm±jfc;内啮合呈现分布于全频域的边频带,位置为:jfm±jfs,jfm±jfs±jfp,jfm±jfsf。内外啮合的边频带分布的差异有助于发现行星齿轮箱局部故障位置。

(3)分析了正常和太阳轮齿根裂纹故障下行星齿轮箱传递路径函数的调制现象规律。时变路径引起啮合频率及其倍频附近的调幅调频现象,时不变路径引起啮合频率及其倍频附近的调幅现象。外啮合的调频规律为nfm±ifp±ifc,内啮合调频规律为nfm±ifp±ifs±ifsf(正常情况下fsf=0)。综合考虑时变和时不变传递路径使得仿真信号边频带与实际信号更加近似。

(4)分析了正常和太阳轮齿根裂纹故障下行星齿轮箱箱体表面振动的信号特征。正常情况下,外啮合能量主要集中在啮合频率附近,内啮合能量主要集中在啮合频率二倍频附近;外啮合与内啮合的阶次谱位置为:jOm±jOp,jOm±jOs。太阳轮裂纹故障下,内外拟合能量主要集中在啮合频率二倍频附近;外啮合阶次谱位置特征无明显变化,内啮合阶次谱位置为:jOm±jOs±jOp,jOm±jOsf。