动态宽卷积残差网络的轴承故障诊断方法

秦国浩 张 楷,2 丁 昆 黄锋飞 郑 庆,2 丁国富,2

1.西南交通大学机械工程学院,成都,6100312.西南交通大学轨道交通运维技术与装备四川省重点实验室,成都,610031

0 引言

轴承作为旋转机械的关键零部件之一,其运行状态直接影响着机械装备的运行状态[1]。在长期的运行过程中轴承承受交变载荷和疲劳损伤,易产生磨损、点蚀、剥落等破坏,以致机械设备停机,造成巨大经济损失和人员伤亡等危害[2]。因此,状态信号监测和智能诊断对轴承长期健康运行具有重要研究意义和应用价值[3]。

以支持向量机、浅层神经网络等为代表的传统机器学习故障诊断方法是将获取的轴承振动信号进行人工特征提取和筛选,然后通过分类器对轴承健康状态进行识别。如杨宇等[4]使用经验模态分解方法提取轴承故障特征进行诊断,完成了对轴承工作状态和故障类别的有效精确识别,但是此类方法存在依赖专家经验、非线性特征提取能力差、故障诊断精度不足等问题。随着计算能力的提高和人工智能的发展,神经网络因其强大的非线性特征自适应提取能力受到机械故障诊断领域的广泛研究[5]。例如,侯文擎等[6]在自编码网络中引入“稀疏”和“损伤加噪”构成了DAE(denosing autoencoder)网络,提取的数据特征鲁棒性强;赵光权等[7]使用深度置信网络对原始时域信号直接进行故障提取和健康状况识别,取得了较高的诊断精度。然而,上述神经网络局部特征提取能力较弱,无法高效提取数据深层表示特征,制约了其在工业中的应用与发展。卷积神经网络为解决此问题而设计的局部感知和权值共享能有效减少模型参数量、抑制过拟合。一些学者也针对一维振动信号作为输入的轴承故障诊断任务进行了适应性改进[8-9]。

近年来,卷积神经网络已成为轴承故障诊断主要智能算法框架之一,许多学者从不同方面对卷积神经网络进行了大量改进,以提高其故障诊断精度。在深度学习理论中,通常认为网络层数的增加有利于深层非线性抽象特征的提取。赵小强等[10]在轴承故障诊断中引入神经网络Alexnet,并将一维振动信号按横向插样构建为二维特征图以保留轴承故障信息卷积运算时域信号的关联性;赵宇凯等[11]使用连续的3×3卷积核替代原本的卷积核,再反复叠加卷积层和池化层增加网络的深度,使得该方法能够更好地提取滚动轴承振动信号的更深层特征;温江涛等[12]使用堆叠的一维卷积自编码的残差结构,搭建无监督领域自适应的迁移学习网络模型,较好地实现了源域到目标域特征知识迁移,提高了轴承故障诊断精度。然而,当网络层数超过一定范围后,网络输入或梯度信息在传播过程中可能会消失,进而导致模型诊断能力下降甚至失效。深度残差网络(deep residual network,ResNet)通过引入跨层连接拟合残差项有效解决了深度神经网络深度增加所带来的梯度消失和梯度爆炸等问题[13]。赵靖等[14]使用残差注意力卷积神经网络方法,有效提取源域故障特征,提高了迁移学习方法下的轴承故障诊断精度。除了增加网络层数,也可将跨层连接扩展至所有层直接相连,以进一步确保网络中各层之间的最大信息流传递[15]。熊鹏等[16]结合动态加权密集连接卷积网络对不同频带信息自适应加权,加强了密集连接卷积网络对变转速工况的特征表征能力,提高了变转速下故障识别率。此外,为使信息感知多样化,采用多尺度卷积设计是一种可行的方案。如吴静然等[17]针对噪声条件下故障识别准确率偏低的问题,提出了一种基于注意力机制的多尺度端到端故障诊断方法;赵小强等[18]也通过引入Inception网络结构和注意力机制对卷积神经网络进行改进,使网络能最大化地提取故障数据中的信息。

以上针对卷积神经网络及扩展网络的改进方法在轴承故障诊断中取得了较好的效果,但在实际工程中,往往不能直接对轴承振动进行接触测量,一些微弱早期故障信号在传递过程中易受到相关部件运行噪声干扰,使得其故障特征淹没在噪声中[19]。而现有诊断模型特征提取范围仍受其卷积核感受野大小的制约,统一尺度的卷积核也难以充分捕捉轴承故障振动信号中的不同冲击频率成分,进而阻碍故障诊断准确率的进一步提高。本文提出一种基于动态宽卷积残差网络(dynamic wide-kernels residual network,DWResNet)的轴承故障诊断方法,该方法在一维深度残差网络基础上引入宽残差核结构形成双通道并行网络结构,并通过注意力机制对卷积核进行动态加权,自适应地充分提取不同尺度特征信息,以实现强噪声背景下轴承故障的高精度诊断。

1 卷积神经网络基础理论

1.1 卷积层

卷积层是卷积神经网络中最为核心的组成部分,每一个卷积层都由多个卷积核组合而成。相较于全连接网络,卷积神经网络具有数据局部感知和权值参数共享等优势,能够有效减少网络的参数量。在输入的振动信号数据上,卷积核通过滑动不同的步长来提取相应位置的局部特征。同时,可以使用一个卷积核来提取不同位置的同类局部特征进行权值共享,从而实现卷积网络中参数量的有效利用。卷积的运算可表示为

(1)

式中,Xl为第l层的输出;W(c)为第c个卷积核的权重矩阵;*为卷积运算;b为权重偏置。

为了使得卷积层具有不同的感受野,可通过设置不同的卷积核大小来实现。卷积核感受野的计算公式为

(2)

式中,Ll为第l层对应的感受野大小;kl为第l层的卷积核大小;si为第i层的移动步长。

1.2 空洞卷积

空洞卷积就是在标准的卷积中加入空洞,扩大卷积层的感受野,且不失对特征的分辨提取能力。在不增加卷积层层数的前提下,通过设置不同的空洞率,形成不同感受野大小的空洞卷积。

假设原来第l-1层的卷积核大小为kl-1,则卷积核空洞率为d的一层空洞卷积的感受野大小Ll为

Ll=kl-1+(kl-1-1)(d-1)

(3)

假设空洞卷积的步长为s,那么经过空洞卷积后的特征图大小m的计算公式为

(4)

式中,x为当前层的输入;p为填充操作的尺寸。

通过设置不同的空洞率d使得原本的卷积核拥有更大的感受野,同时配合填充操作,使得输出的特征图大小m能够与原卷积层输出的特征图大小一致,从而保证不同卷积核输出的特征图能够进行信息融合。

对于一维的滚动轴承振动信号,通过设置空洞卷积能够使得网络在提取不同特征区间有效信息的同时保证网络参数量的缓慢增长。

1.3 残差网络(ResNet)

ResNet的提出使得在网络深度增加的同时获得更高的收益成为可能。ResNet不是直接学习多层堆叠的函数拟合的直接映射,而是学习它们的残差映射。图1展示了一个标准的残差结构(x表示输入,σ表示激活函数),通过学习F(x)函数的残差映射而非直接映射F(x)+x来有效减少网络由于深度增加带来的梯度问题以及对直接映射的过拟合问题。

图1 标准的残差块Fig.1 Residual block

ResNet模型的核心部分由许多基本的残差块堆叠而成,如图2所示。每一个基本残差块中,均由两个卷积层、两个ReLU[20]激活函数、两个批量正则化(batch normalization,BN)[21]和一个恒等映射连接而成。当前后通道数发生改变时,通过一个图2b所示的卷积层来适配改变的通道数。其中,采用BN层的目的是为了加快网络收敛,提高网络的泛化性,它的计算公式如下[21]:

(5)

式中,E[x]为x的期望;Var[x]为x的方差;γ、β均为可训练的超参数;ε为一个趋近于0的常量。

ReLU是常见的激活函数,其主要作用是减小网络计算量,缓解过拟合,其计算公式如下:

(6)

通过上述残差连接的结构可使得网络向更深的层次发展,同时也能一定程度地缓解网络的退化、梯度消失和梯度爆炸等问题。

2 本文所提方法

为了使得网络更易于提取振动信号的特征信息,减少信号强噪声干扰所带来的影响,本文提出了动态宽卷积残差网络对轴承振动信号进行学习。具体来说,本文首先在残差网络的基础上,对残差块的每层卷积进行改进,然后引入可选择核网络(selective kernel networks,SKNet)[22]中可选择性操作进行改进,使得网络能够在3×1的卷积核和宽核的空洞卷积之间进行自适应的选择,最后按照不同的权重融合两个不同卷积核的输出特征作为每层的输出特征进行学习。

2.1 动态宽卷积残差网络(DWResNet)

本文所提方法的单层结构如图3所示,对于任意一个给定的特征图输入X(X∈RC×H×W,C为输入数据的维度,H、W分别为输入数据的高和宽),将其同时输入到两个卷积核大小分别为3×1和空洞率d为14的3×1空洞卷积中,使其在扩大感受野的同时减少参数量的增长。在经过两个卷积变换之后得到两个特征图:

UA=FA(X)

(7)

UB=FB(X)

(8)

其中,F为对应的卷积变换函数。然后,将得到的两个卷积核大小不同(其中一个为宽卷积核)的特征图UA和UB拼接进行信息融合,得到的融合特征表示为

U=Concat(UA,UB)

(9)

类似于SE模块[23]的结构,将得到的融合特征通过全局平均池化(global average pooling,GAP)操作在特征图上进行低维特征融合,以保留特征图的主要特征,同时减小网络的计算量,防止网络的过拟合。该过程的计算公式为

(10)

由于输入为一维数据,则高度H为1。

然后再通过一个全连接层(fully connected-layers,FC)将其以r的压缩率压缩,使其成为具有全局感受野的实数向量。向量的长度为C/r,S为GAP操作后的输出,压缩操作后的输出为

(11)

式中,B为批量正则化层;W为全连接层权重。

在压缩后,通过两个全连接层分别将压缩的输出扩张为原始维度(ZA和ZB),然后通过Softmax操作进行权值归一化,得到不同卷积核和不同通道的权值A和B:

(12)

(13)

根据这样两个不同的权重值,可自适应地选择不同空间尺度上的信息。将归一化之后的不同的权重乘以对应的特征图,可得到最终加权之后由网络自适应选择的输出:

Y=AUA+BUB=A′+B′

(14)

本文所提方法中的每个残差块的卷积层都使用了可选择的宽卷积核,使得网络能够在提取特征的每一个阶段都能够自适应地选择合适的卷积核进行卷积,并且通过宽卷积核的压缩扩张处理达到信号降噪的功能。此外,还修改了网络中的通道数为8、16、32、64,以减小网络的参数量,提高网络的训练效率。

2.2 所提网络模型的结构

图4展示了所提模型的整体结构。该模型以18层的残差网络为基础,对其中所有残差块中的卷积层进行改进,整个网络由第一层的卷积、16个改进的卷积层和一个全连接层组成,其具体结构参数如表1所示。

图4 所提方法网络模型结构Fig.4 Structure diagram of the proposed method network

每个改进卷积层的结构如图3所示。在数据输入网络时,首先对数据进行卷积操作,再输入到后续网络层中。后续网络层按照残差连接的方式分为两种不同的残差块。在输入输出特征通道不改变时,使用残差块1依次经过卷积层、批量正则化、激活函数、卷积层和批量正则化后直接与原始输入特征进行连接。在输入输出通道改变时,使用残差块2经过几个与残差块1相同的操作之后,将输入特征进行卷积,以匹配改变的通道数。最后得到提取的特征,输入全局平均池化层进行特征信息的融合,经过全连接层输出最后分类结果。

2.3 所提方法故障诊断流程

本文所提方法的轴承故障诊断具体流程如图5所示。轴承故障诊断可大致分为4个步骤:①利用加速度传感器采集轴承试验台数据,为数据集添加不同信噪比的高斯白噪声以模拟噪声输入,并划分构建相应的训练集和测试集;②构建DWResNet,并将所有训练样本进行预处理,按批量输入到网络中进行模型训练;③在训练的过程中,通过交叉熵损失函数进行反向传播,对网络权重参数进行优化迭代;④将测试数据集输入训练完成的网络中,输出滚动轴承故障诊断结果。

图5 所提方法的故障诊断流程Fig.5 Fault diagnosis process of the proposed method

3 实验验证

3.1 实验数据集介绍

3.1.1实验一

本文采用德国帕德博恩大学(PBU)轴承数据集[24]对所提方法进行验证。该试验台的详细设置请参考文献[24]。试验台设置如图6所示,所有测试轴承的型号均为6203,采样频率为64 kHz。

图6 帕德博恩大学轴承试验台[24]Fig.6 The test rig of PBU[24]

本实验中使用的数据集的具体工况设置如表2所示,本数据集包含了5种故障,每个故障类型下的数据都处理为表3所示数据。当轴承的损伤深度为D∈(0,2] mm时,设置为损伤等级1;当轴承的损伤深度D∈(2.0,4.5] mm时,设置为损伤等级2。

表2 帕德博恩大学轴承数据所选工况参数

表3 帕德博恩大学轴承数据详细信息

3.1.2实验二

为验证本文方法的有效性,本文还采用了动力传动故障诊断综合实验台(drivetrain diagnostic simulator,DDS)[25]所采集的数据进行实验验证。实验台设置如图7所示,在平行齿轮箱轴承中,设定电机固定频率为20 Hz,采样频率为12.8 kHz。每类故障工况重复实验4次,每次采集各方向的振动加速度信号共204 800个点。本数据集包含了内圈、外圈、滚动体故障和复合故障等4种故障类型。

图7 动力传动故障诊断综合实验台[25]Fig.7 Power transmission fault diagnosis comprehensive experimental bench[25]

3.2 实验环境及模型参数设置

本实验中,样本长度设置为4096,通过滑窗的方式截取样本。在实验一中,滑窗步长与样本长度相等,因此样本之间无重叠。其中,每类样本1200条,并按1∶1的比例划分训练集和测试集,详细信息见表3。实验二中,样本长度也设置为4096,通过滑窗截取了每类样本600条,滑窗步长为582,并按1∶1的比例划分训练集和测试集。

分别在信噪比(signal to noise ratio,SNR)为-4,-2,0,2,4 dB的高斯白噪声以及无人为添加噪声情况下,对卷积神经网络(CNN)[26]、VGG-16[27]、首层宽卷积深度神经网络(WDCNN)[28]、ResNet、首层宽卷积的残差网络(WResNet)和本文所提方法进行了对比实验,每组实验的超参数设置相同,但在实验一、实验二中设置初始学习率分别为0.01和0.1。并且为保证训练精度和损失函数收敛,在使用CNN和VGG-16方法时设置学习率为固定值,详情见表4,每组实验重复10次以保证实验结果的准确性。同时,针对不同大小的宽卷积核,设置了空洞率d分别为1、2、14、26和38。信噪比的计算公式如下:

(15)

式中,PSignal、PNoise分别为原始信号和噪声的能量。

以正常状况为例,经过加噪后的部分信号如图8所示。实验运行环境为Windows系统和Intel(R) Xeon(R) Silver 4210R CPU @2.40GHz处理器,使用了基于Python(3.9)的Pytorch 深度学习框架构建所提方法和对比方法模型,并采用NVIDIA GeForce RTX 3090 GPU进行训练加速。

(a)无人为添加噪声 (b)RSNR=4 dB

3.3 实验结果分析

3.3.1实验一结果分析

在实验一中,根据实验结果得到表5(表中“无”表示无人为添加噪声)。由表5可知,虽然在没有人为添加噪声的情况下,不同方法均能保持较高的诊断准确率,但是随着噪声干扰程度的增加,不同方法的诊断准确率也随之降低,说明了强噪声干扰对模型的抗噪性要求较高,例如CNN的诊断准确率在RSNR=-4 dB的情况下比无噪声情况下降低了11.29个百分点。区别于其他的方法,本文所提方法仅降低了1.99个百分点,在各个不同噪声情况下,所提方法能够准确地提取出滚动轴承的振动信号特征,具有更高的稳定性。

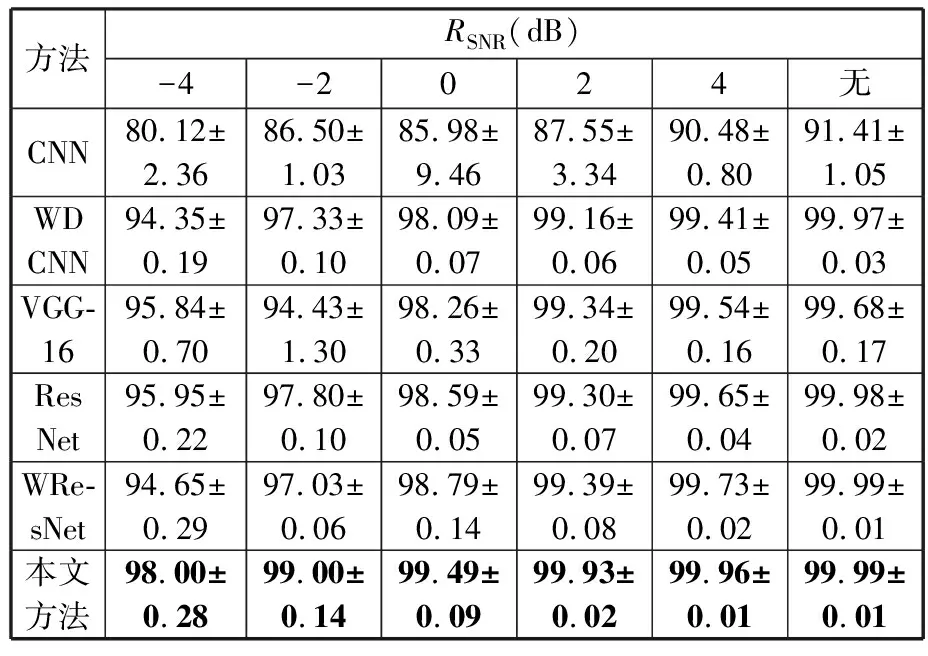
表5 实验一诊断准确率结果

对比CNN、VGG-16和ResNet在同一噪声下的诊断精度可以看出,网络深度的增加对滚动轴承故障特征的提取能力和稳定性均有一定提高。当然,层数并非越深越好,超过一定数量后将造成梯度爆炸或梯度消失等问题。对比CNN、WDCNN和WResNet可以发现,卷积核宽度的增大对网络容噪具有较好的效果。同样地,需要选择适当的网络宽度和网络深度,使得方法能够在轴承故障诊断上有更有效的结果。

由对比实验结果可知,本文提出方法具有较优的容噪能力,能够在噪声环境下拥有显著提高的滚动轴承故障分类能力和模型的稳定性。本文所提方法在不同噪声水平情况下均有较好的诊断准确率,特别是在RSNR=-4 dB的强噪声干扰下,相较于CNN、WDCNN、VGG-16、ResNet和WResNet,诊断准确率分别提高了17.88、3.65、2.16、2.05和3.35个百分点。同时,本文所提方法在不同噪声干扰下的诊断标准差相较于其他方法均较小,表示它在强噪声下具有较高的模型稳定性。

为了探究强噪声信号对模型分类边界形成的影响,以RSNR=-4 dB为例,绘制了本文所提方法在网络不同阶段所提取故障特征的t-SNE可视化聚类图,如图9所示。由图9不难看出,输入的强噪声原始信号呈现极为严重的混淆、重叠现象,导致难以直接聚类辨识。随着数据经过更深层的阶段2、3、4,网络对不同健康状况的分类边界逐渐清晰。阶段4时,同类故障特征的类内聚集程度显著提高,模型的分类边界也最为明显。这说明经过多个阶段的模型训练,所提方法能够有效提取强噪声下不同类别的故障特征,较小冗余噪声的干扰,从而提高对目标轴承的诊断精度。

(a)输入 (b)阶段2输出

同时,为进一步展示不同方法对各个健康状况的详细辨识能力,图10展示了RSNR=-4 dB下不同方法辨识结果的混淆矩阵。图10显示,不同方法在辨识分类的过程中对NC和OR2两类健康状况是较为容易辨识的,但是对OR1、IR1和IR2三类故障难以有效辨别,分析其可能的原因是外圈故障和内圈故障特征相似,且两个不同故障等级的内圈故障特征相似。本文所提出的方法虽然也存在上述情况,但是相较于其他方法,本文方法对难诊断类别的诊断准确率最高,说明了所提方法能够有效提高不同故障类型中判别性特征的辨识能力,从而提高诊断准确率。

(a)CNN (b)WDCNN

为了进一步分析不同空洞率对模型诊断效果的影响,以强噪声RSNR=-4 dB为例,分别设置空洞率d为1、2、14、26和38,并进行相应的故障诊断实验,结果如图11所示。由图11不难看出,所提方法在d取14时,得到了高达98%的诊断准确率,这说明本文所选超参数较为合适,能使模型具有较高的噪声鲁棒性。由于空洞率的大小直接决定了感受野的大小,这也印证了单一地提高空洞率对噪声工况下轴承故障诊断准确率的提高并不是绝对的,需要选择合适的空洞率对数据进行更为全面的特征提取,以获得更丰富的分类辨识信息,进而提高轴承故障诊断的准确率。

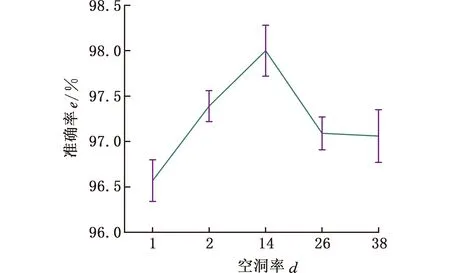
图11 RSNR=-4 dB下不同空洞率下所提方法诊断准确率Fig.11 Diagnostic accuracy of the proposed method at RSNR=-4dB for different d

3.3.2实验二结果分析

根据实验二实验结果绘制相应的精度直方图,见图12,可以看出,在各个不同等级的RSNR下,本文方法相较于其他方法精度均有一定程度的提高,并且具有较好的稳定性。RSNR=-4 dB时的诊断准确率相较于无添加噪声时,在各个方法下分别降低16.26、8.16、16.91、8.84、9.53和5.39个百分点,由此可见本文所提方法的诊断效果受到噪声的影响最小,印证了本文所提方法对强噪声的鲁棒性。并且本文所提方法在RSNR=-4 dB时的标准差绝对值相较于其他方法最小,验证了本文所提方法的稳定性。

图12 实验二结果直方图Fig.12 Histograms of experiment 2 results

4 结论

针对滚动轴承在强噪声干扰下故障诊断提取特征能力较差、辨识能力不足的问题,提出了一种基于动态宽卷积残差网络的轴承故障诊断方法。该方法通过可选择的宽卷积层对不同噪声干扰下的滚动轴承监测信号进行故障特征提取,通过生成的自适应权重自动地为网络选择使用卷积核,在网络深度加深的同时保证了网络的抗噪能力。

实验结果表明,相较于CNN、WDCNN、VGG-16、ResNet和WResNet等网络,本文所提方法具有更高的诊断准确率。在无人为添加噪声情况下,本文所提方法在实验一中能够取得99.99%的诊断准确率;而在信噪比为-4,-2,0,2,4 dB下,该方法依然可取得99.28%的平均准确率。并且实验二的结果也印证了本文所提方法的有效性。因此,本文所提方法具有较高的辨识能力、抗噪能力和泛化能力,可为实际工业强噪声干扰条件下的轴承故障诊断提供一定的参考借鉴。