真假辨析,发展学生核心素养*
——关于全等三角形中“SSA”的再思考
⦿ 安徽省太湖县实验中学 周志宽
《义务教育数学课程标准(2022年版)》指出:通过数学学习,学生逐步会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界.笔者下面以一道初中几何命题的真假辨析为例,结合“一般观念”,谈谈一线数学教师在教学中该如何贯彻新课程理念,在“三会”中发展学生数学核心素养.
1 问题呈现
沪科版数学教材八年级(上)第14章,在三角形全等判定方法的探究中,“SSA”即两边及其中一边的对角分别相等的两个三角形全等是假命题,可以举如下反例:
如图1,在△ABC中,作BD=BA交AC于点D,但△ABC与△DBC不全等.
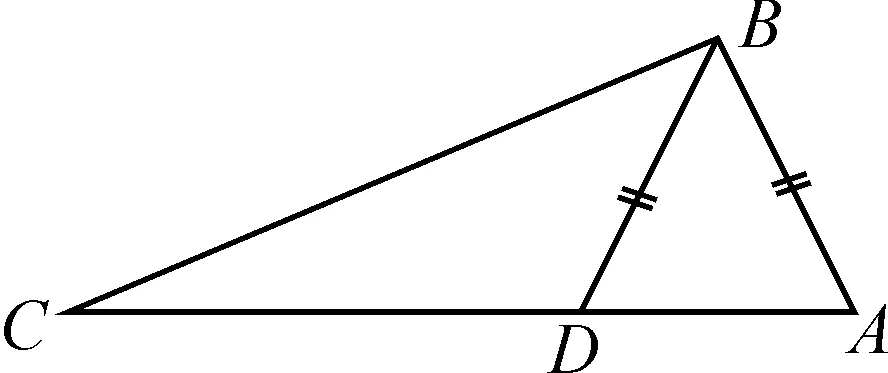
图1
在什么情况下,两边及其中一边的对角分别相等的两个三角形会全等呢?
已知在△ABC与△A1B1C1中,AB=A1B1,BC=B1C1,∠C=∠C1,试探究满足什么条件△ABC与△A1B1C1全等?
2 问题探究
探究1:若∠C=∠C1=90°,△ABC与△A1B1C1一定全等吗?
方法一:通过平移,两个三角形可拼成一个等腰三角形,可得一锐角相等,再运用“AAS”可证.说明这两个三角形均为直角三角形时,它们一定全等.
证明:在平面内移动△ABC,使点B和点B1、点C和点C1重合,点A和点A1在B1C1的两侧,如图2.
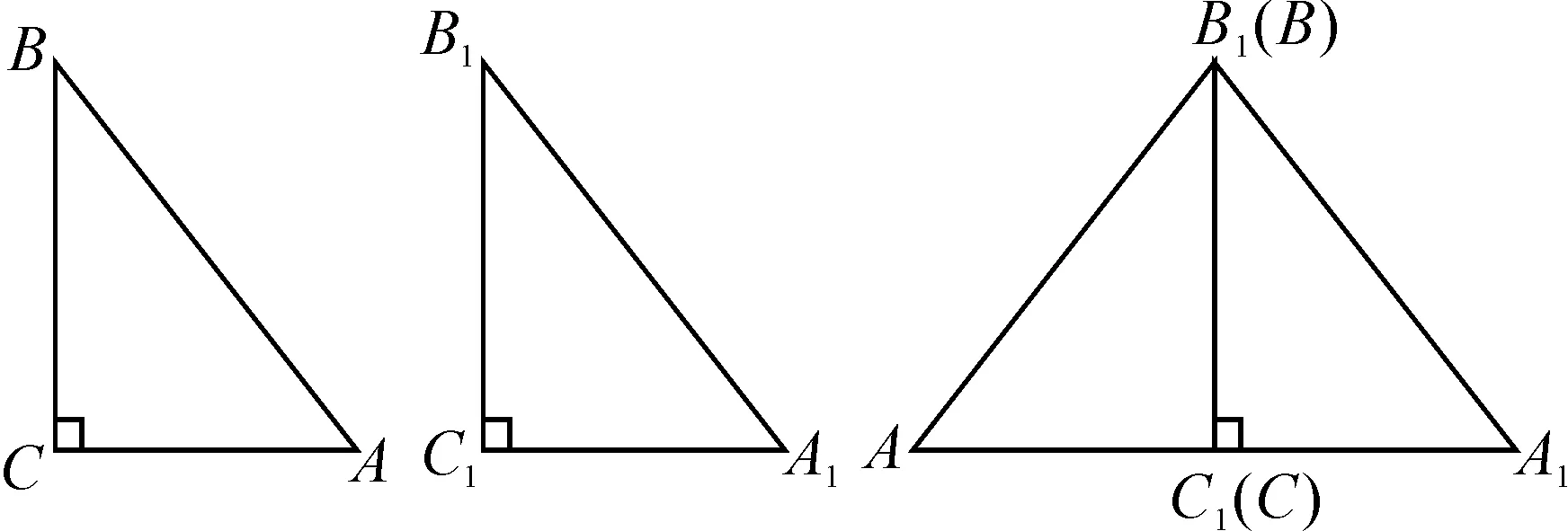
图2
由∠A1C1A=∠A1C1B1+∠ACB=90°+90°=180°,可知A1,C,A三点在同一条直线上.
又B1A=B1A1,所以∠A=∠A1.
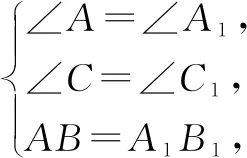
方法二:根据勾股定理在直角三角形中由两边相等可证第三边相等,再用“SSS”可证.
结论1:斜边和一条直角边分别相等的两个直角三角形全等(“HL”).
探究2:若∠C=∠C1<90°,△ABC与△A1B1C1全等吗?
类似于图1,同样可构造不全等的两个三角形作为反例,则△ABC与△A1B1C1不一定全等.
探究3:若△ABC与△A1B1C1均为锐角三角形,两三角形一定全等吗?
分析:如图3,过点B,B1分别作BD⊥CA于点D,B1D1⊥C1A1于点D1,可证△BCD≌B1C1D1,得BD=B1D1;再证Rt△ABD≌Rt△A1B1D1,得∠A=∠A1,可证△ABC≌△A1B1C1.则两三角形一定全等.
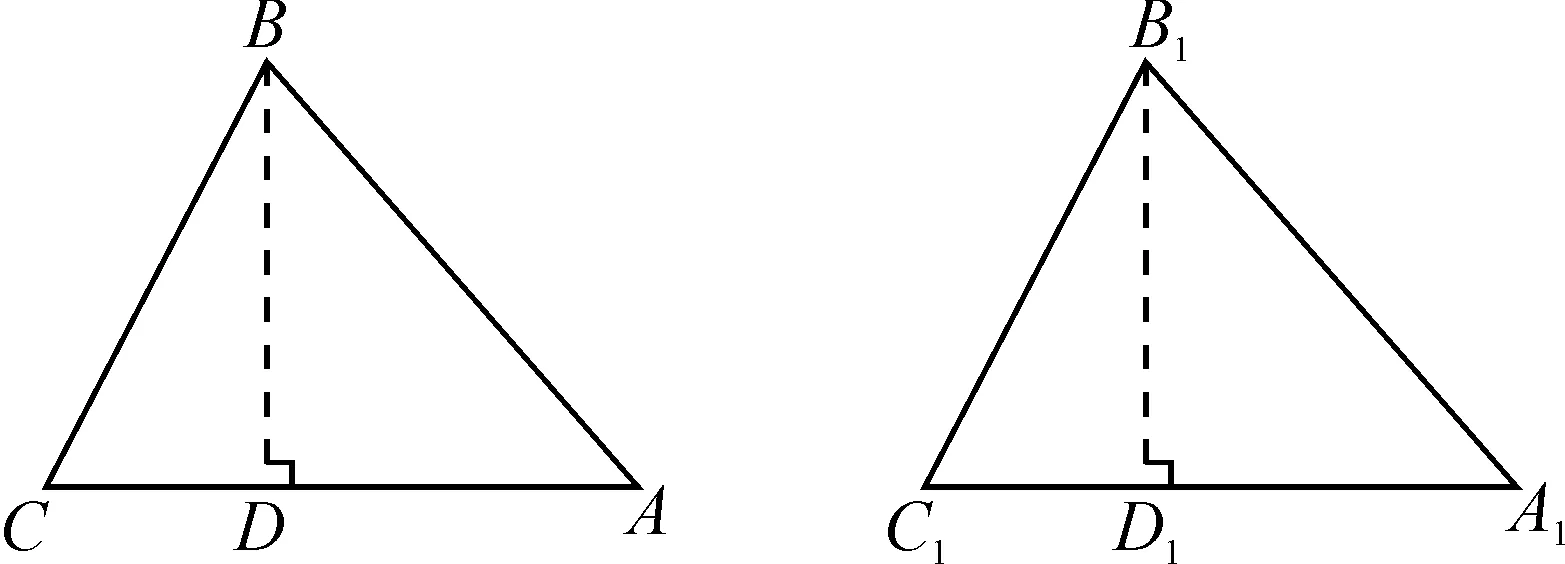
图3
证明:过点B,B1分别作BD⊥CA于点D,B1D1⊥C1A1于点D1.则∠BDC=∠B1D1C1=90°.
在△BDC与△B1D1C1中,
∴△BDC≌B1D1C1(AAS).
∴BD=B1D1.
易证Rt△ABD≌Rt△A1B1D1(HL).
∴∠A=∠A1.
在△ABC与△A1B1C1中,
∴△ABC≌△A1B1C1(AAS).
结论2:两边及其中一边的对角(对角是锐角)分别相等的两个三角形不一定全等,但两边及其中一边的对角分别相等的两个锐角三角形一定全等.
探究4:若△ABC与△A1B1C1均为钝角三角形,两个三角形一定全等吗?
不一定全等.反例:如图4,△ABA1中,∠ABA1=90°,且BA=BA1,延长AA1至点C,连接BC.则△CBA与△C1B1A1均为钝角三角形.
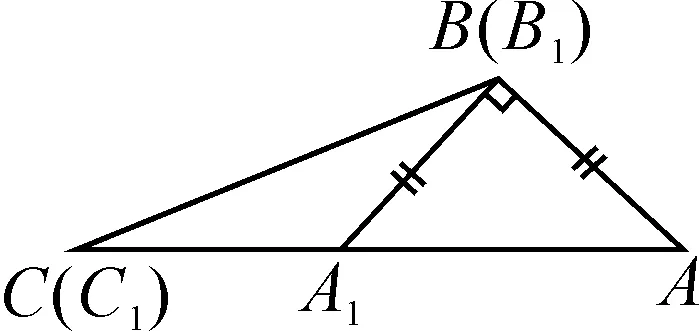
图4
探究5:若∠C=∠C1>90°,△ABC与△A1B1C1一定全等吗?
如图5,过点B,B1分别作BD⊥CA交AC的延长线于点D,B1D1⊥C1A1交A1C1的延长线于点D1,可证△BCD≌B1C1D1,得BD=B1D1.用“HL”再证Rt△ABD≌Rt△A1B1D1,得∠A=∠A1,即可证△ABC≌△A1B1C1.
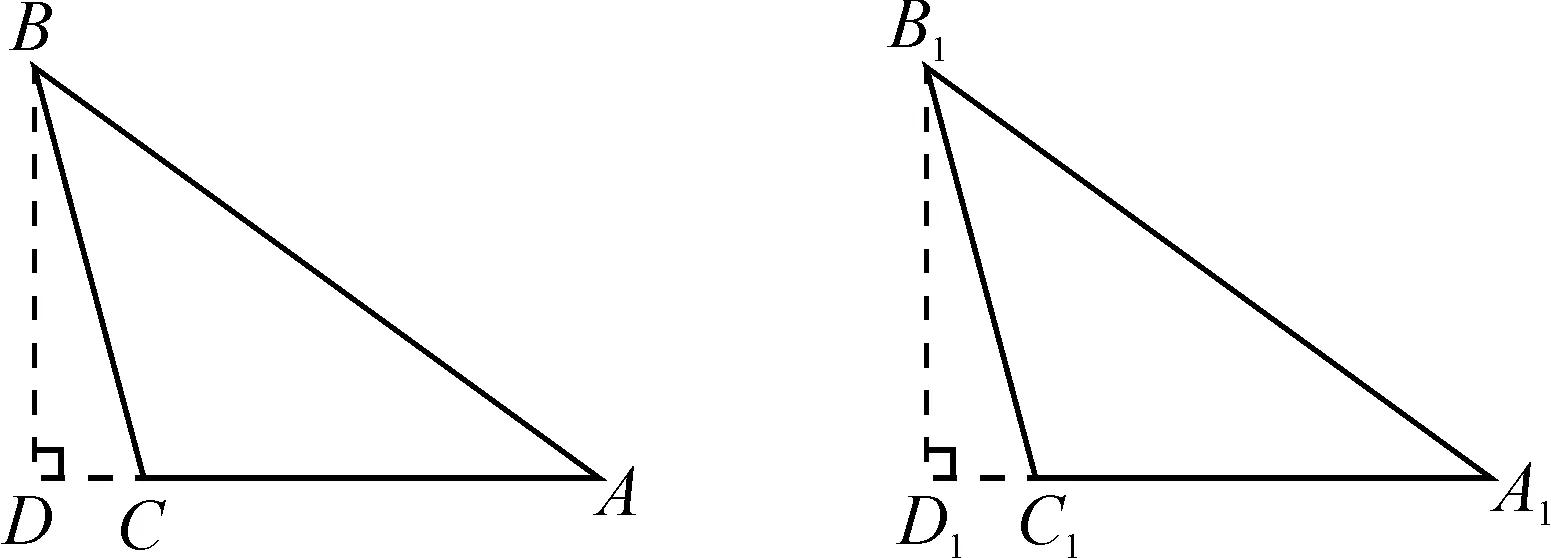
图5
结论3:两边及其中一边的对角分别相等的两个钝角三角形不一定全等,但对角是钝角时,对应的两个三角形一定全等.
3 延伸应用
在△ABC中,过∠BAC角平分线上任意一点P,分别作PE⊥AB于点E,PF⊥AC于点F,若BE=CF,试判断AB一定等于AC吗?并说明理由.
分析:解决该问题的关键是画图.需考虑点E,F在AB,AC上的位置及点P与△ABC的位置关系.借助几何画板探究,当点E,F同时在AB,AC上或同时在其延长线上,AB一定等于AC.如图6,其中点P位于BC上(左一),通过两次证全等即可,此种情况最特殊,证明最简单;后三种情况连接PB,PC可以转化,同理可证.
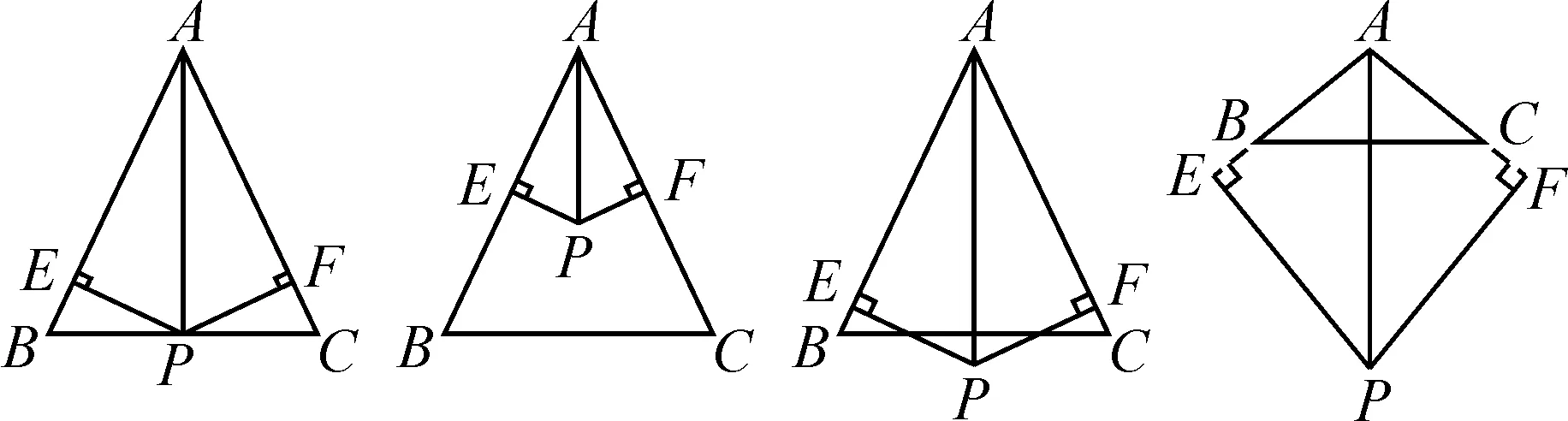
图6
当点E,F不同时在AB,AC上或不同时在其延长线上,AB一定不等于AC,如图7.
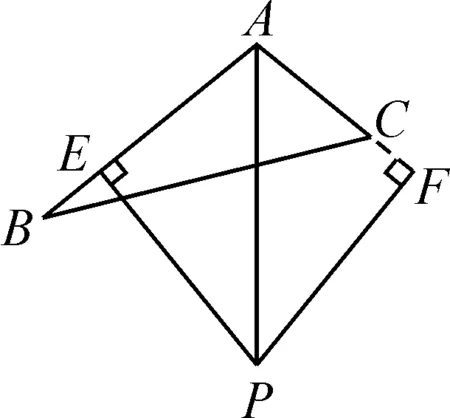
图7
综上,AB不一定不等于AC.
4 研究感悟
4.1 会用数学的眼光观察现实世界
由探究可知,“两边及其中一边的对角分别相等的两个三角形全等”是假命题;若对角是直角或钝角,则两个三角形一定全等,若对角是锐角则不一定全等;若在直角三角形或锐角三角形中,则两个三角形一定全等,若在钝角三角形中则不一定全等.这几个命题,真真假假,教学中只有让学生亲身体验,经历分析和比较的过程,感悟共性,分辨差异,才能看清问题的本质,形成合适的类,通过几何直观提升抽象能力,会用数学的眼光观察现实世界.
4.2 会用数学的思维思考现实世界
在解决问题的过程中,真命题的证明都运用了“一般观念”中分类、转化、由特殊到一般的数学思想,充分利用已有元素探究两个三角形中其他元素是否唯一确定.以上问题情境充分运用“一般观念”引导学生经历几何命题发现、猜想、证明的过程,感悟归纳推理和演绎推理的传递性,会用数学的思维思考现实世界.
4.3 会用数学的语言表达现实世界
从问题呈现、猜想、证明、归纳体现出研究数学问题的基本套路.对于两个假命题,均举反例说明;对于真命题,运用演绎推理予以严密论证,体现了严谨的科学精神.通过引导学生经历针对图形性质、关系、变化确立几何命题的过程,体会数学命题中条件和结论的表述,会借助图形分析条件与结论之间的逻辑联系,感悟数学表达的准确性和严谨性,发展模型观念,会用数学的语言表达现实世界.
中国科学院院士张景中在《走进教育数学》中指出,数学教育工作者应致力于“把数学解题变容易”的研究.因此,尽可能在教学中寻求更通用、更有力的解题方法,以“一般观念”引领,借助现代信息技术,为学生提供有章可循的解决问题的途径,“把数学变容易”,真正实现减负增效.

