一题四法证明“动”线与“定”线垂直

■成都经济技术开发区实验中学校 杜海洋

空间中的垂直关系有:线线垂直、线面垂直、面面垂直。垂直关系始终是立体几何考查的重点,从近些年高考来看,以多面体为载体,重点考查空间垂直的位置关系一直是立体几何命题的热点。一般来讲,线线垂直是主要的也是最基本的情况,在三者转化的过程中穿针引线,无论是线面垂直还是面面垂直,都源于线与线的垂直,这种转化为“低维”垂直的思想方法,在解题时非常重要,尤其涉及动直线与定直线的垂直问题,其思维聚焦点更显特殊。下面,笔者通过一道高考真题来展示线线垂直的证明策略。

真题呈现(2021 年全国甲卷)如图1,已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,|AB|=|BC|=2,E,F分别为AC和CC1的 中 点,D为棱A1B1上的点,BF⊥A1B1。证明:BF⊥DE。

图1

分析：通过已知条件,确定三条互相垂直的直线,可建立合适的空间直角坐标系,借助空间向量证明线线垂直;由于本题涉及“动”直线与“定”直线的垂直关系,解答的思维难度和灵活度较大。

证法1(补形法)

因为BF⊥A1B1,A1B1//AB,所 以BF⊥AB。

因为AB⊥BB1,BF∩BB1=B,所 以AB⊥平面BCC1B1。

|AB|=|BC|=2,构造 正 方 体ABCGA1B1C1G1,如 图2 所 示,过E作AB的平行线分别与AG,BC交于其中点M,N,连接A1M,B1N。

图2

因为E,F分别为AC和CC1的中点,所以N是BC的 中 点,易 证Rt△BCF≅Rt△B1BN,则∠CBF=∠BB1N。

又因为∠BB1N+∠B1NB=90°,所以∠CBF+∠B1NB=90°,BF⊥B1N。

又因为BF⊥A1B1,B1N∩A1B1=B1,所以BF⊥平面A1MNB1。

又因为ED⊂平面A1MNB1,所以BF⊥DE。

点评:要证线线垂直,可转化证线面垂直。因为本题DE为动直线,所以解题目标要将直线DE放在一个平面内,通过证BF垂直此平面从而获得证明。

证法2(几何法)

如图3,取BC的中点N,连接EN,B1N,所以EN//AB,即EN//A1B1,则EN//DB1,即 四 边 形ENB1D为平面四边形。要 证BF⊥DE,即 证BF⊥平面ENB1D。

图3

由证法1 可得BF⊥B1N,BF⊥AB,所 以BF⊥EN。

又因为EN∩B1N=N,所以BF⊥平面ENB1D。

因为ED⊂平面ENB1D,所以BF⊥DE。

点评:此法的实质与证法1一样,依然构造平面,先建立线面垂直,再推出线线垂直。证法1与证法2都是将动直线DE放在一个平面内,通过证BF垂直此平面从而获证。由于直线DE为动直线,构造三角形形成平面行不通,所以构造一组对边平行的四边形是解决问题的关键。

证法3(坐标法)

同证法1,易得BA,BC,BB1两两垂直。则以B为坐标原点,分别以BA,BC,BB1所在直线为x轴,y轴,z轴建立空间直角坐标系,如图4。则B(0,0,0),A(2,0,0),C(0,2,0),B1(0,0,2),A1(2,0,2),C1(0,2,2),E(1,1,0),F(0,2,1)。

图4

由题意,设D(a,0,2)(0≤a≤2)。

点评:由题意得出此几何题属于典型的“墙角模型”,即建立空间直角坐标系,利用坐标运算实现目标数量积为0,从而获得证明。解答涉及“墙角模型”的立体几何试题,建立坐标系是较简便的解法。

证法4(基底法)

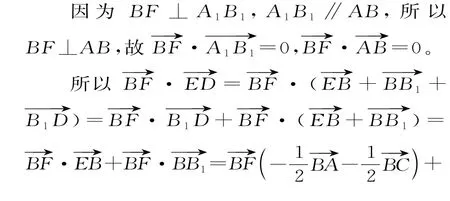
点评:基底法的本质是将所求向量运算关系转化为题中已知模长、夹角的两个向量运算关系,核心是转化思想,能用坐标法就可以用基底法,坐标是建立在特殊的基底之上的,所以由证法3 就应该想到证法4。

总之,由于立体几何中的很多问题都可以通过“化空间为平面”的思想方法来解决,因此通过作图转化为平面几何中证明线线垂直的方法最为常见。常用到的知识有:勾股定理,菱形或正方形的对角线互相垂直,等腰三角形的三线合一,直径所对的圆周角是直角,三角形全等,过切点的半径垂直于切线等等。所以在证明过程中寻找相应的“点”进行连线是解决问题的关键。垂直问题在立体几何中占有重要的地位,是历年高考命题的热点,空间中的垂直关系常转化为证明线线垂直。因此,同学们一定要把证明线线垂直的方法研究透彻。