空间向量与立体几何单元测试（A 卷）答案与提示

一、单项选择题

1.C 2.C

3.B 提示:设圆锥底面的半径为r,则由题意知,而L=2πr,代入得π≈。

4.D 提示:为了便于解题,将正四面体A-BCD放入正方体中,如图1 所示。连接HG,OD。

图1

对于选项A,若E,F分别为AB,CD的中点,则易知EF⊥CD,选项A不正确;

对于选项B,在正方体中,易知CD⊥平面ABHG。因为过点D且与平面ABHG平行的平面不经过点E,所以不存在E,使得DE⊥CD,选项B不正确。

对于选项C,在正方体中,易证OD⊥平面ABC,所以不存在E,使得DE⊥平面ABC,选项C不正确。

对于选项D,设OD与平面ABC的交点为K,连接CK,只要令平面CDK与AB的交点为E即可得平面CDE⊥平面ABF,选项D 正确。

5.C 提示:连接AB,CD。

(1)当点P在CA的延长线上,即点P在平面α与平面β的同侧时,如图2。

图2

因为α//β,平面PCD∩平面α=AB,平面PCD∩平面β=CD,所 以AB//CD,△PAB～△PCD,

因|PA|=6,|AC|=9,|PD|=8,故,解得|BD|=。

(2)当点P在线段CA上,即点P在平面α与平面β之间时,如图3。类似(1)的方法。可得

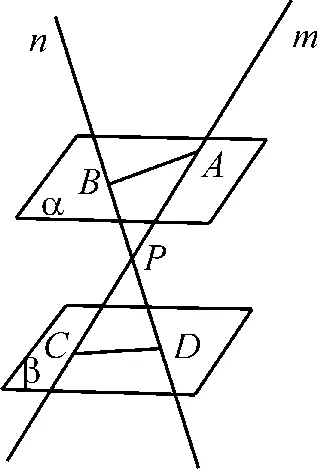
图3

因|PA|=6,|PC|=|AC|-|PA|=9-6=3,|PD|=8,故

,解得|PB|=16,则|BD|=|PB|+|PD|=24。

6.B

图4

8.A

二、多项选择题

9.BD

10.ABCD 提示:以正八面体的中心O为原点,OB,OC,OE分 别 为x轴,y轴,z轴,建立如图5所示空间直角坐标系。

图5

设正八面体的边长为2,则A(0,-,0),E(0,0,),C(0,,0),D(-,0,0)F(0,0,-)。

又AB//CD,AB⊄平面CDF,CD⊂平面CDF,则AB//平面CDF。

由AB∩AE=A,AE,AB⊂平面ABE,所以平面AEB//平面CDF,B正确。

易知平面ACE的一个法向量为n1=(1,0,0),平面BDF的一个法向量为n2=(0,1,0)。

因为n1·n2=0,所以平面ACE⊥平面BDF,D 正确。

因为AP⊥BP,AP⊥CP,所以AP⊥平面BCD。

又AP⊂平面BAD,可得平面BAD⊥平面BCD,C正确。

12.AD 提示:对于A,平面ABC截勒洛四面体所得截面如图6。它的面积为三个半径为4,圆心角为60°的扇形的面积减去两个边长为4的正三角形的面积。

图6

对于B,如图7,取CD中点G,在△ABG中,|AG|=|BG|=,|AB|=4,记该勒洛四面体上以C,D为球心的两球交线为弧AB,则该弧是以CD的中点G为圆心,以为半径的圆弧。

图7

设圆心角为∠AOB=α,则cosα=,可知α·2≠π,所以弧长不等于,B错误。

对于C,如图8,设弧AB的中点是M,线段AB的中点是N,设弧CD的中点是H,线段CD的中点是G,则根据图形的对称性,M,N,G,H四点共线且过正四面体A-

图8

对于D,勒洛四面体能容纳的最大球,与勒洛四面体的弧面相切,如图7,其中点E为该球与勒洛四面体的一个切点,由对称性可知O为该球的球心,内半径为OE,连接BE,易知B、O、E三点共线。设正四面体A-BCD的外接球半径为r,如图9,则由题意得为正四面体A-

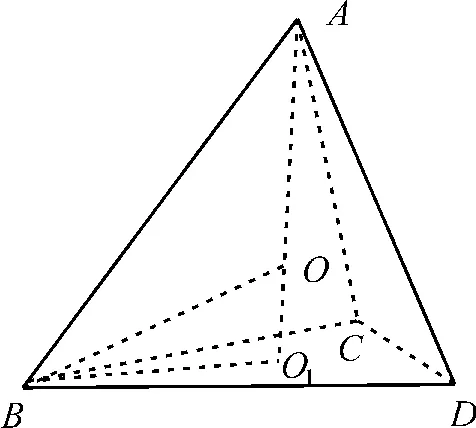
图9

三、填空题

13.3π 提示:如图10,取AB中点O,连接OC,OD。在△ABD中,由|AD|=1,,得|AD|2+|BD|2=|AB|2,则AD⊥BD。又 平 面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,故AD⊥平面BCD,即AD⊥BC。在△BCD中,|BC|=|CD|,|BD|=,即|BC|2+|CD|2=|BD|2,则BC⊥CD。因为AD∩CD=D,所以BC⊥平面ACD,BC⊥AC。则O为三棱锥A-BCD的外接球的球心,外接球的半径。球O的表面积为3π。

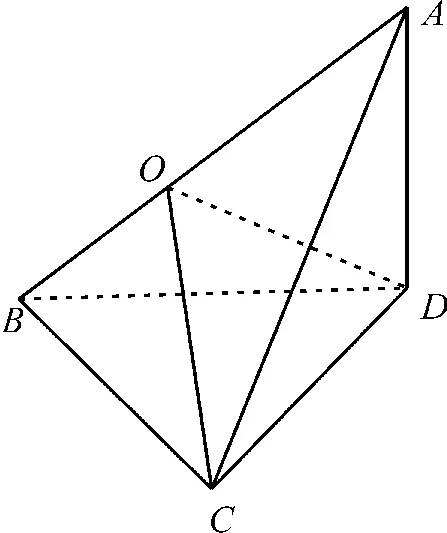
图10

14.4 提示:连接AC,交BD于点O,连接OP。以O为原点,OA所在直线为x轴,OB所在直线为y轴,OP所在直线为z轴,建立空间直角坐标系,如图11。

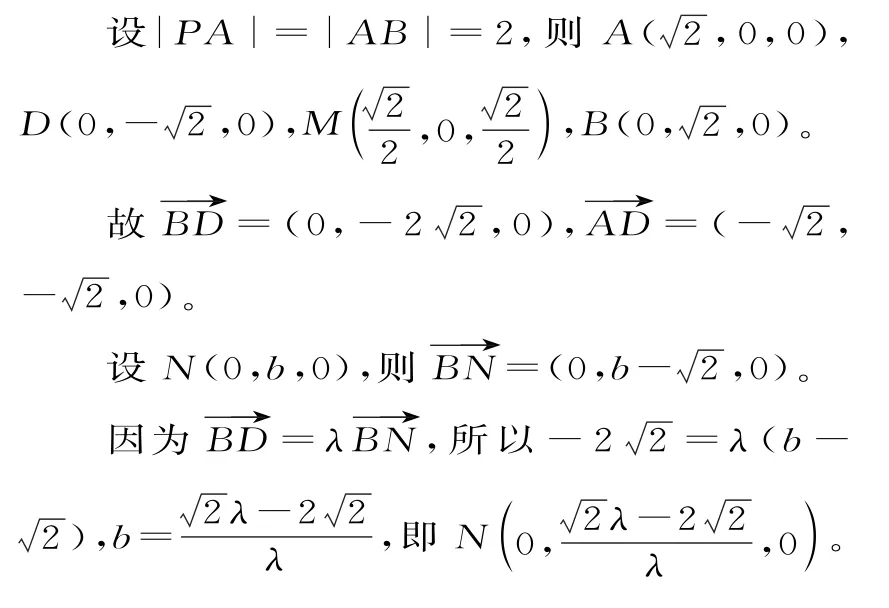
图11

因MN⊥AD,故=0,解得λ=4。

如图12,设正四面体的棱长为a,E为△BCD的中心,故AE⊥平面BCD。

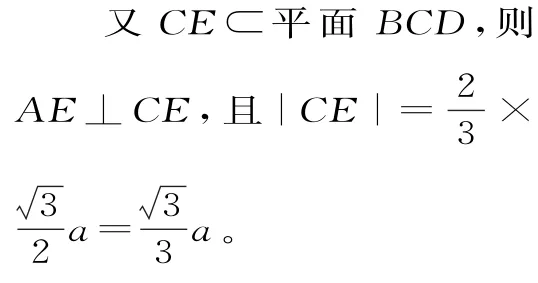
图12

小球半径|OF|=r=1,则OF⊥AC,大球半径|OA|=R,|AC|=a。

16.①③ 提示:对于①,连接AD1,CD1。由正方体的性质知△ACD1为等边三角形,O为底面ABCD的中心,故O为AC的中点,AC⊥D1O,①正确。

对于②,将D1O进行平移到过B1点,使之与B1P具有公共顶点,如图13,根据立体图形判断,无论如何也不可能满足B1H平行或重合于B1P,所以D1O不可能与B1P平行,②错误。

图13

对于③,取B1B的中点E,连接OE,EC,BD,D1E,如图13。易证明D1O⊥平面OEC,所以P在线段EC上运动,当点P到点E位置时,|C1P|最大,△D1C1P的面积最大为,③正确。

对于④,P到直线D1C1的距离为线段PC1的长度,所以|PC1|=|PB|,判定出P点在线段BC1的垂直平分线上,④错误。

四、解答题

17.(1)如图14,作AP⊥CD于点P,分别以AB,AP,AO所在直线为x轴,y轴,z轴建立空间直角坐标系,则A(0,0,0),

图14

设平面OCD的法向量为n=(x,y,z)。

取z=1,解得

又MN⊂平 面OCD,从 而MN//平 面OCD。

18.(1)因 为AA1⊥平 面ABC,AB,AC⊂平面ABC,所 以AA1⊥AB,AA1⊥AC。而AB⊥AC,故建立如图15所示的空间直角坐标系。设|A1M|=a,a∈[0,1],则

图15

A(0,0,0),A1(0,0,1),B(1,0,0),C(0,1,0),B1(1,0,1),M(0,a,1)。

(2)设平面BCM的法向量n=(x,y,z)。

取x=1,得n=(1,1,1-a)。

19.(1)因为PA⊥平面ABCD,CD⊂平面ABCD,所以PA⊥CD。因为AD⊥CD,PA∩AD=A,PA⊂平面PAD,AD⊂平面PAD,所以CD⊥平面PAD。

(2)以A为原点,在平面ABCD内过A作CD的平行线为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,如图16。

图16

则A(0,0,0),E(0,1,1),P(0,0,2),B(2,-1,0)。

平面AEP的一个法向量为n=(1,0,0),平面AEF的一个法向量为m=(x,y,z)。

设二面角F-AE-P的平面角为θ,由图可知θ为锐角,则

故二面角F-AE-P的余弦值为。

(3)存在这样的λ。

若A,E,F,G四点共面,则AG在平面AEF内。

存在这样的λ=,使 得A、E、F、G四点共面。

20.(1)如图17,以O为原点,OA,OB,OP所 在 直 线 分 别 为x轴、y轴、z轴 建 立 空间直角坐标系,不妨设AB=2,则可得B(0,2,0),C(-2,0,0)。

图17

因为BC∩PB=B,A1E⊄平面PBC,所以A1E//平面PBC。

(2) 由 (1) 知 △PBC的 重 心,则

若点O在平面PBC内的投影恰好为△PBC的重心,则:解得k=。

所以当k=时,点O在平面PBC内的投影恰好为△PBC的重心。

21.(1)在图18中,连接CE。

因为DC//AB,CD=AB,E为AB的中点,所以DC//AE,且DC=AE,四边形ADCE为平行四边形,|AD|=|CE|=|CD|=|AE|=2。同理可证|DE|=2。

在图19中,取DE的中点O,连接OA,OC,则|OA|=|OC|=。

图19

因为|AD|=|AE|=|CE|=|CD|,所以DE⊥OA,DE⊥OC。

因 为OA∩OC=O,OA,OC⊂平 面AOC,所以DE⊥平面AOC。

因为AC⊂平面AOC,所以DE⊥AC。

(2)若选择①:由(1)知DE⊥平面AOC,DE⊂平面BCDE,所以平面AOC⊥平面BCDE,且交线为OC。

过点A作AH⊥OC交OC于 点H,则AH⊥平面BCDE。

若选择②:因为DC//EB,所以∠ACD即为异面直线AC与EB所成的角。

在 △ADC中, cos ∠ACD=,所以|AC|=。而|OA|2+|OC|2=|AC|2,即OA⊥OC。

因为DE⊥平 面AOC,DE⊂平 面BCDE,所以平面AOC⊥平面BCDE,且交线为OC。又OA⊂平面AOC,所以AO⊥平面BCDE。

22.(1)如图20,在圆柱O1O2中,AE//CG,AE⊄平面O1CG,CG⊂平面O1CG,故AE//平 面O1CG。

图20

连接DO1,因为等腰梯形ABCD为底面圆O1的内接四边形,|AD|=|DC|=|BC|=1,所以∠AO1D=∠CO1D=∠BO1C=。

则△AO1D为正三角形,故∠O1AD=

因AD⊄平面O1CG,O1C⊂平面O1CG,故AD//平面O1CG。

又AE∩AD=A,AE,AD⊂平 面ADE,故平面ADE//平面O1CG。

(2)如图21,以O1为坐标原点,在底面圆O1内过点O1垂直于平面ABFE作直线为x轴,以O1B,O1O2为y轴,z轴,建立空间直角坐标系。

图21

由于|AD|=|DC|=|BC|=1,|CG|=1,由(1)可知|AO1|=1。