例谈立体几何综合题中的建系策略

■广东省兴宁市第一中学 蓝云波

立体几何综合问题的常见解题方法有两种,即传统方法与空间向量方法。由于传统方法对同学们的空间想象能力要求较高,加之需根据题意作出辅助线,故对不少同学来说具有一定的挑战。因此利用空间向量方法解决立体几何综合问题是很多同学的首选,而空间向量坐标法是空间向量方法中最常使用的方法,解题的基础是要根据题中的条件建立恰当的空间直角坐标系。随着高考对同学们的综合素养的能力要求越来越高,高考涌现出越来越多灵活多变的考题,对大家如何建立空间直角坐标系也提出了更高的要求。因此,如何建系成为同学们成功解决立体几何综合问题必须迈过的一道坎。为帮助同学们彻底解决这个问题,本文探究并总结出建系的四种常见策略,以期对同学们学习有所帮助,从而达到提高大家的数学素养与能力的目的。

一、借助三条两两垂直的直线建系

例1(福建省部分地市2023 届高三第一次质量检测)如图1,在直三棱柱ABC-A1B1C1中,|AC|=,AB⊥BC,E,F分 别 为BB1,CA1的 中 点,且EF⊥平面AA1C1C。

图1

(1)求|AB|的长;

(2)若|AA1|=,求二面角C-A1E-A的余弦值。

解析：(1)因为EF⊥平面AA1CC1,且A1C⊂平面AA1CC1,所以EF⊥A1C。

又因为F为A1C的中点,所以|EA1|=|EC|。

又在Rt△A1B1E、Rt△BEC中,|BE|=|EB1|,易证得△A1B1E≌△CBE,故|A1B1|=|BC|。

因为|AB|=|A1B1|,所以|AB|=|BC|。

又因为AB⊥BC,|AC|=,所以|AB|=1。

(2)以点B1为原点,建立如图2 所示的空间直角坐标系B1-xyz。

图2

不妨设m=(x0,y0,z0)是平面CA1E的一个法向量,那么即

令z0=2,得

又B1C1⊥平面A1B1BA,故1,0)是平面A1B1BA的一个法向量。

设α为二面角C-A1E-A所成的平面角,则,即二面角C-A1E-A的余弦值为。

点评:本题第二问中,由已知条件可知B1B,B1A1,B1C1三条直线两两垂直,故可直接建立空间直角坐标系进行求解。这是立体几何综合题中最容易想到的建系方法,只要同学们基础知识扎实,计算能力过关,即可实现问题的求解。

二、借助线面垂直建系

1.以垂线的垂足为坐标原点建系

例2(山东省青岛市2023届高三一模)如图3,在Rt△PAB中,PA⊥AB,且|PA|=4,|AB|=2,将△PAB绕直角边PA旋转到△PAC处,得到圆锥的一部分,点D是底面圆弧BC(不含端点)上的一个动点。

图3

(1)是否存在点D,使得BC⊥PD? 若存在,求出∠CAD的大小;若不存在,请说明理由。

(2)当四棱锥P-ABDC体积最大时,求平面PCD与平面PBD夹角的余弦值。

解析：(1)当D为圆弧BC的中点,即∠CAD=时,BC⊥PD。

证明如下:因为D为圆弧BC的中点,所以∠CAD=∠BAD=,即AD为∠CAB的平分线。因为|AC|=|AB|,所以AD为等腰△CAB的高线,即AD⊥BC。

因 为PA⊥AB,PA⊥AC,AB∩AC=A,AB,AC⊂平面ABDC,所以PA⊥平面ABDC,故PA⊥BC。

因为PA∩AD=A,所以BC⊥平面PAD,则BC⊥PD。

(2)由(1)得,PA为四棱锥P-ABDC的高。因为|PA|=4,所以当面积S四边形ABDC取最大值时,四棱锥P-ABDC体积最大。设∠CAD=α,则在平面ABDC内过A作直线AE⊥AB,交圆弧BC于点E。由题意知AE,AB,AP两两垂直,则以A为原点,分别以AE,AB,AP所在直线为x轴,y轴,z轴,建 立如图4所示的空间直角坐标系。

图4

则A(0,0,0),P(0,0,4),B(0,2,0),D,1,0),C(,-1,0),则(-,1,0)。

设平面PCD的法向量为n=(x1,y1,z1),则

点评:本题第二问对四棱锥P-ABDC体积最大值的处理是解题的一大障碍,可通过三角形的面积公式与三角恒等变换进行解决,对同学们具有一定的挑战性。在建系时,发现有垂直于平面ABDC的垂线PA,可以点A为原点,PA为z轴,AB为y轴,过点A且与AB垂直的直线为x轴建立空间直角坐标系,这是立体几何综合题中常见的建系方式,应引起大家足够的重视。

2.以底面直角顶点为坐标原点建系

例3(江苏省南通市2023 届高三二模)如图5,在△ABC中,AD是BC边上的高,以AD为折痕,将△ACD折 至△APD的 位 置,使得PB⊥AB。

图5

(1)证明:PB⊥平面ABD;

(2)若|AD|=|PB|=4,|BD|=2,求二面角B-PA-D的正弦值。

解析：(1)因为AD是BC边上的高,所以PD⊥AD,AD⊥BD。

因 为PD∩BD=D,PD,BD⊂平 面PBD,所以AD⊥平面PBD。

因为PB⊂平面PBD,所以AD⊥PB。

又 因 为PB⊥AB,AD,AB⊂平 面ABD,AD∩AB=A,所以PB⊥平面ABD。

(2)如图6,以D为坐标原点,DA所在直线为x轴,DB所在直线为y轴,过点D且与PB平行的直线为z轴,建立空间直角坐标系。|AD|=|PB|=4,|BD|=2,则B(0,2,0),P(0,2,4),A(4,0,0),D(0,0,0)。

图6

点评:本题建系时,由于平面ABD中有两条相互垂直的直线AD,BD,故以点D为坐标原点,DA所在直线为x轴,DB所在直线为y轴,过点D且与PB平行的直线为z轴建系。这是有线面垂直条件的另一种常见的建系方法,值得大家细细品味。

三、借助面面垂直建系

1.利用面面垂直的性质定理得到的垂线为z 轴建系

例4(山东省济南市2023 届高三下学期开学考试)如图7,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB//CD,AB⊥AD,侧 面PAD⊥底 面ABCD,|DP|=|DA|=|DC|=AB。

(1)证明:平面PBC⊥平面PAB;

(2)若|AD|=|AP|,求平面PAC与平面PAB夹角的余弦值。

解析：(1)由题意,取M,N分别为棱PA,PB的中点,连接DM,MN,NC,如图8所示。

图8

则MN//AB,|MN|=|AB|。因为CD//AB,且|CD|=|AB|,所以MN//CD,且|MN|=|CD|,故四边形MNCD为平行四边形,DM//CN。

因为|DP|=|DA|,M为棱PA的中点,所以DM⊥PA。

因为AB⊥AD,平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,所以AB⊥平面PAD。

因为DM⊂平面PAD,所以AB⊥DM。

又AB∩PA=A,且AB,PA都在平面PAB内,所以DM⊥平面PAB。

因为DM//CN,所以CN⊥平面PAB。又因为CN⊂平面PBC,所以平面PBC⊥平面PAB。

(2)由题意及(1)得,取AD的中点O,连 接PO。 因 为△PAD为等边三角形,所 以PO⊥AD。因为平面PAD⊥底面ABCD,所 以PO⊥底面ABCD。过O作OE//AB,交BC于点E,则OE⊥AD。以O为原点,OA,OE,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图9所示。

图9

设|AD|=2,则P(0,0),A(1,0,0),D(-1,0,0),C(-1,2,0)

故平面PAC与平面PAB夹角的余弦值为。

点评:本题建系时,可以根据侧面PAD⊥底面ABCD这个条件,通过逻辑推理得PO⊥平面ABCD,则可以以O为原点,PO所在直线为z轴进行建系。

2.以底面的直角顶点为坐标原点建系

例5(广东省佛山市2022届高三二模)如图10,在以P,A,B,C,D为顶点的五面体中,平面ABCD为等腰梯形,AB//CD,|AD|=|CD|=|AB|,平面PAD⊥平面PAB,PA⊥PB。

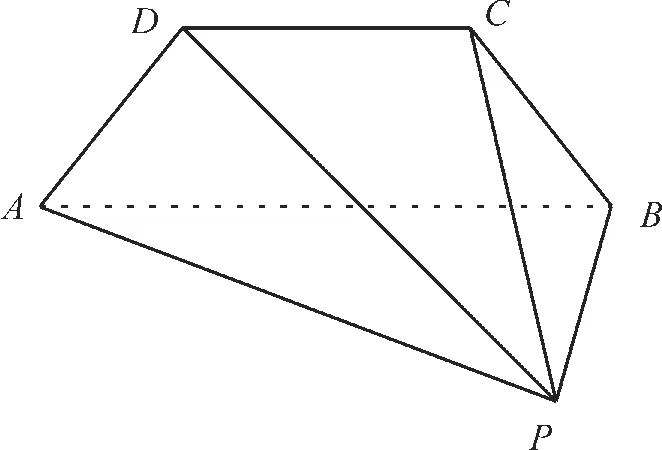
图10

(1)求证:△PAD为直角三角形;

(2)若|AD|=|PB|,求 直 线PD与平面PBC所成角的正弦值。

解析：(1)在等腰梯 形ABCD中,作DH⊥AB于H,连 接BD,如图11。

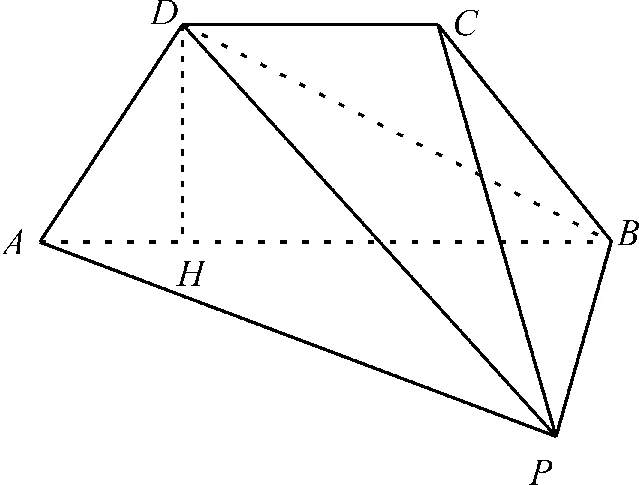
图11

因平面PAD⊥平面PAB,平面PAD∩平面PAB=PA,PB⊂平面PAB,而PA⊥PB,所以PB⊥平面PAD。

又AD⊂平面PAD,于是有AD⊥PB。PB∩BD=B,PB,BD⊂平面PBD,则有AD⊥平面PBD。PD⊂平面PBD,因此,AD⊥PD,△PAD为直角三角形。

(2)在平面PAD内 过 点P作Pz⊥PA。因平面PAD⊥平面PAB,平面PAD∩平面PAB=PA,故Pz⊥平面PAB。因此,PB,PA,Pz两两垂直,以点P为原点,建立如图12所示的空间直角坐标系。

图12

点评:本题也有面与面垂直的条件,由于PA⊥PB,故建系时,为方便得出点的坐标,可以P为原点,PA,PB所在直线分别为x,y轴进行建系。本题的难点是如何得出点D的坐标,实际上可过点D作PA的垂线,结合几何关系得到。

四、借助二面角建系

例6(山东省潍坊市2022 届高三一模)图13 是 由 矩 形ACC1A1、等边△ABC和平行四边形ABB1A2组成的一个平面图形,其中|AB|=2,|AA1|=|AA2|=1,N为A1C1的中点。将其沿AC,AB折起使得AA1与AA2重合,连接B1C1,BN,如图14。

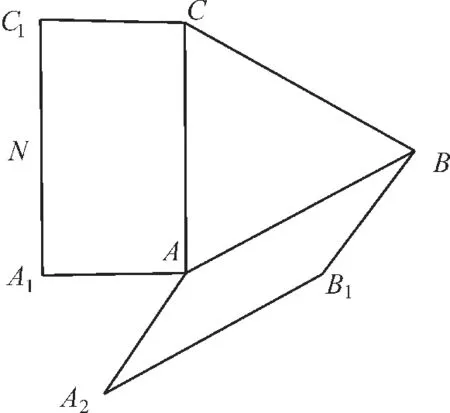
图13

图14

(1)证明:在图14 中,AC⊥BN,且B,C,C1,B1四点共面;

(2)在图14中,若二面角A1-AC-B的大小为θ,且tanθ=-,求直线AB与平面BCC1B1所成角的正弦值。

解析：(1)取AC的中点M,连接NM,BM,如图15。

图15

因ACC1A1为矩形,N为A1C1的中点,故AC⊥MN。

又因△ABC为等边三角形,则AC⊥MB。MN∩MB=M,MN,MB⊂平面BMN,则AC⊥平面BMN。

又BN⊂平 面BMN,所 以AC⊥BN。矩形ACC1A1中,AA1//CC1,平行四边形ABB1A1中,AA1//BB1,因此,BB1//CC1,所以B,C,C1,B1四点共面。

(2)由(1)知MN⊥AC,BM⊥AC,则∠NMB为二面角A1-AC-B的 平 面 角,θ=∠NMB。在平面BMN内 过M作Mz⊥MB,有AC⊥Mz,以M为坐标原点建立如图16所示的空间直角坐标系。

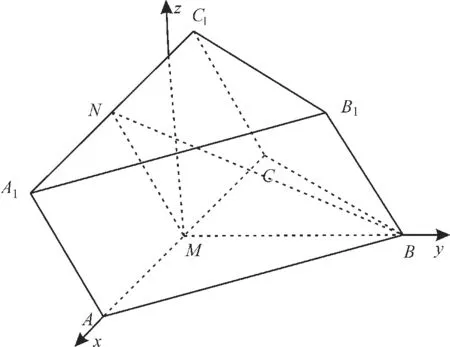
图16

所以直线AB与平面BCC1B1所成角的正弦值是。

点评:本题是一道极具创新的试题,建系也具有一定的难度。结合题意,可作出二面角A1-AC-B的平面角,由于AC⊥平面MNB,故可以以点M为坐标原点,MA,MB所在直线分别为x,y轴,在平面MNB内过点M且与平面ABC垂直所在的直线为z轴建系。当表示点N,C1时,可结合三角函数的定义求出其坐标,对同学们的创新能力提出了较高的要求,这也是新高考喜欢考查的方式,值得大家细细感悟。