面向电力线通信的干扰态检测及极化码设计

马 涛，葛红舞，孙圣武，戴 欣，夏重阳

(1.南京南瑞信息通信科技有限公司，江苏 南京 211106 2.国网江苏省电力有限公司淮安供电分公司，江苏 淮安 223022 3.南京邮电大学 通信与信息工程学院，江苏 南京 210003)

电力线载波通信是指直接利用电力线传输信息的一种通信方式，由于建设成本低、覆盖范围广等优势，在电力信息采集、电力监控以及智能家居等领域得到了广泛应用［1－8］。 鉴于电力线最初是为输送电能设计的，其信道特性相对恶劣。 电力线上脉冲噪声很常见，它是由整流器、开关电源及电源开关瞬时启闭等引起的，其噪声特性与无线通信中的有很大不同［2－3，5，7］。 为此，如何对抗脉冲干扰噪声是电力线载波通信需要解决的关键技术。

信息论的奠基人香农指出，纠错编码是对抗噪声并有效逼近信道容量的主导技术。 Turbo 码、低密度校验（Low-Density Parity-Check，LDPC）码以及极化（Polar）码是目前3 种主流的逼近信道容量纠错编码技术，其中，极化码的提出时间最晚，也是唯一一种理论上被严格证明能达到加性高斯白噪声（Additive White Gaussian Noise，AWGN）信道容量的纠错编码方式［9－11］。

Turbo 码和LDPC 码的主流解码算法是置信度传播算法，而极化码的解码一般采用连续消除（Successive Cancellation，SC）译码算法及其变种SCL（Successive Cancellation List）译码算法［10］。 目前，在中短码长下，极化码及其解码算法得到了广泛应用，如5G 移动通信标准就采用了Polar 短码。

不同于无线通信信道中的高斯白噪声，电力线载波通信中的脉冲干扰噪声通常采用Middleton Class-A Noise（MCAN） 模 型 进 行 建 模［1－5］。 虽 然Turbo、LDPC 以及Polar 码被证明能有效逼近AWGN 信道的容量，但对于MCAN 信道并没有一般性的结论。 为此，文献［12－14］研究了MCAN 信道下的Turbo 码译码问题，通过MCAN 统计特性提出的译码算法，相比常规译码算法能取得显著增益。文献［15］研究了非规则LDPC 码作为外码对MCAN信道进行纠错的设计问题，通过RS 码与LDPC 码的级联，有效提高了电力线载波通信的传输能力。 文献［1，4－5］针对MCAN 信道设计了中短Polar 码，基于SC 译码实现了一定的编码增益。 目前，虽然MCAN 信道的编译码取得了很多进展，但文献所报道的纠错编译码技术方案还缺乏系统性。

文献［16］基于马尔可夫模型将MCAN 信道容量分解为多个干扰态的信道容量与非干扰态信道容量的线性加权叠加，且系统信道容量主要决定于非干扰态信道容量。 本文从该观点出发，较为系统地挖掘信道状态检测对极化码设计以及译码性能的影响，通过对数似然比首次推导了信道状态检测准则，并基于干扰状态的信道删除机理，给出了脉冲干扰信道下极化码的一种设计准则。

1 系统模型

1．1 极化码

极化码是一种线性分组码，对于码长N ＝2n、信息比特长度为K的极化码，其码字c ＝［c1，c2，…，cN］ 生成方式可表示为

极化码编码设计的目标是确定信息比特的位置集合I∈｛1，2，…，N｝，以使得给定信道条件下译码性能最优。 Arikan［10］的研究表明，等效比特信道在式（1）的编码以及SC 译码下有所谓的极化现象：等效比特信道的互信息要么趋于1，要么趋于0。 互信息大的等效比特信道集合正是编码需要确定的集合I。

1．2 脉冲干扰噪声信道模型

本文的电力线脉冲干扰噪声模型采用MCAN模型，假设信息比特在极化码编码后采用BPSK 调制，经过电力线载波信道后的接收基带信号可以表示为

其中，zk表示MCAN 噪声，其由背景AWGN 噪声以及脉冲噪声组成，即

其中

1．3 马尔可夫信道建模及其容量分析

由式（2）和式（3）可知，MCAN 信道可以被建模成马尔可夫模型，在该马尔可夫模型下，信道在k时刻的状态Sk作为一个随机变量，其取值空间为集合｛s0，s1，s2，…｝，其中sm对应Ok ＝m（见式（3））的情形，MCAN 信道处于状态sm的概率为

根据二元MCAN 以上的马尔可夫模型，不难求得其遍历信道容量［15］

其中

表示MCAN 处于状态sm的二元输入信道容量。

以具体二元MCAN 信道为例，在A ＝0．1，Γ＝0．1，Eb／N0＝2 dB 的条件下，经计算可得信道的遍历容量C ＝0．915 4， 各个状态的概率及其对应容量Cm为

π0C0＝0．904 7，已经非常逼近信道的遍历容量C ＝0．915 4，为有效逼近MCAN 信道的传输容量，一个有用的策略是对信道状态进行检测，然后通过纠错编码有效逼近无干扰状态（状态s0） 下的信道容量。

2 接收信号预处理与极化码设计

2．1 接收信号的对数似然比计算

为译码方便起见，一般需要计算信道接收信号的对数似然比。 针对二元MCAN 信道模型（2），该对数似然比可以推导如下

定义如下函数

则式（9）可以改写为

其中，指数求和的对数函数可以通过式（12）进行快速求解。

2．2 信道状态检测与删除信道

通过二元MCAN 容量的分析可知，二元MCAN的信道可以分解为无干扰状态和干扰状态，而干扰状态又可根据干扰强度变量Ok进行细分。 给定一组接收信号矢量y ＝［y1，y2，…，yN］，根据检测与估计理论，信道k时刻的最佳状态估计为最大后验概率估计，即

由于MCAN 的遍历容量主要取决于非干扰态的信道容量，对干扰态进行细分检测的实际意义并不大。 为此，信道状态检测可以采用以下对数似然比进行估计

其中

当LSk ＜0 时，判断该时刻k处于干扰态，即干扰态的判断条件为

如以上条件满足，则相应时刻的接收样本被认为处于干扰态，译码时直接将相应的样本删除，或者直接将该时刻的对数似然比值置0，即ek ＝0；如果处于非干扰态，则ek ＝1。 对一个码字内的接收样本进行状态检测，得到删除矢量

本文假设二元MCAN 的极化码设计是基于接收信号的对数似然比值进行删除后的矢量，即

接收信号在译码前的预处理详细流程如图1所示。

图1 接收信号译码前的预处理

2．3 二元MCAN 信道的极化码设计

设二元MCAN 信道转移函数为

其中，X ＝｛＋1，－1｝ 表示二元输入（BPSK），Y表示信道输出符号集，W（y ｜x），x∈X，y∈Y表示转移概率。 信道W的Bhattacharyya 参数定义为

在极化码的SC 译码下，第i个比特的等效信道定义为

Arikan［10］证明了等效信道W（i）N的Bhattacharyya参数满足如下的迭代计算不等式

鉴于图1 所示的接收信号预处理，二元MCAN信道的接收信号经过预处理后可以用BEC 信道有效逼近，且等效BEC 信道的删除概率为

最终本文针对上述二元BEC 信道进行极化码设计，并用于二元MCAN 信道。 结合图1 的信号预处理，所设计的极化码取得了优异的性能。

3 仿真与分析

3．1 实验设置

实验中采用的二元MCAN 信道的参数设置如下：A ＝0．1，Γ＝0．1。 该 信 道 的 遍历 容量C ＝0．915 4，π0＝0．904 8。 所设计的极化码码率R ＝0．5，码长N＝512。 实验中采用等效BEC 信道设计极化码，其删除概率为∊＝1－ π0＝0．095 2。

3．2 结果比较

文献［1］针对电力载波通信的二元MCAN 信道讨论了几种极化码的构造算法并进行了性能仿真。在以上同等实验设置条件下的仿真性能如图2所示。

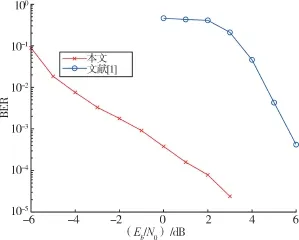
图2 本文与文献［1］的结果比较

文献［1］ 中的构造算法（Heuristic Based Capacity SD）通过MCAN 的噪声分布（4）直接计算Bhattacharyya 参数Z（W），在此基础上构造极化码。不同于文献［1］，本文主要采用了基于对数似然比的预处理，并采用干扰态的概率作为删除概率设计相应BEC 的极化码。 由图2 可知，在BER ＝10－4下本文结果相比文献［1］有4 dB 以上的增益。

3．3 预处理增益

本文提出的信号预处理，是基于MCAN 信道的马尔可夫模型导出的有关信道状态的检测准则，该检测准则结合信道的对数似然比及其删除能有效保留非干扰态的信息。 图3 给出了在相同极化码下采用和不采用预处理（对应于图1 中是否删除）的性能差异。

图3 本文所提预处理的译码增益

如图3 所示，在相同极化码下采用本文提出的预处理方法，在BER ＝10－3处所得到的增益在6 dB以上。

4 结束语

本文面向电力载波通信的脉冲干扰噪声信道，提出了一种极化码编译码解决方案。 该方案基于脉冲干扰噪声信道的马尔可夫模型，提出一种对数似然比的信道状态检测算法，该算法可以有效检测信道是否处于干扰态。 在此基础上，本文基于BEC 等效信道设计出的极化码在采用预处理的译码算法下，相较于文献报道性能大幅提升，在BER ＝10－4下，码率＝1／2、码长＝512 的极化码，相比文献［1］结果提高4 dB 以上。