采用混合多址技术的卫星系统反向链路遍历容量分析

郭 焱，孔槐聪，廖向荣，林 敏，欧阳键

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003 2.中国移动（苏州）软件技术有限公司，江苏 苏州 215009)

卫星通信具有覆盖范围广、通信质量好等优点，不仅可以作为地面移动通信网的有效补充，还可以为偏远和人口稀少地区提供性能最佳和最全面的网络覆盖，为城市环境中的高密度人口区域提供高带宽低成本覆盖，为自然灾害地区用户提供应急通信服务，成为第6 代（6th Generation， 6G）移动通信的一个研究热点，并且被认为是构建空天地海一体化信息网络不可或缺的一种手段，受到了工业界和学术界的高度重视［1－5］。 目前，国内外学者围绕卫星通信领域的各个方面，尤其是性能分析做了很多富有价值的工作。 例如，假设卫星链路服从阴影莱斯（Shadowed-Rician， SR）分布的情况下，文献［6］分析了采用放大转发（Amplify-and-Forward， AF）协议的卫星通信系统中断性能。 文献［7］针对采用译码转发（Decode-and-Forward， DF）协议的卫星通信系统，推导出误码率的精确闭合表达式。 文献［8］研究了采用时分多址（Time Division Multiple Access，TDMA）技术的多用户卫星通信系统，并在卫星采用门限判断AF 协议的条件下分析了系统的中断概率。 文献［9］针对基于最优调度方案的卫星系统，推导了中断概率和遍历容量的闭合表达式。 需要指出的是，上述研究仅考虑正交多址接入（Orthogonal Multiple Access， OMA）的场景，在这种情况下，系统正交地分配通信资源，存在资源利用率低的问题，难以为大量用户提供接入服务［10－11］。 因此，如何进一步提高频谱效率是卫星通信领域的一个技术难题。

非正交多址接入（ Non-orthogonal Multiple Access， NOMA）技术通过引入非正交频谱资源和多用户干扰，借助接收端的连续干扰消除（Successive Interference Cancellation， SIC）技术，可以实现在同一个资源块中对多个用户的同时接入，从而显著提高频谱效率和用户的公平性［12］。 国内外很多学者已经将NOMA 方案应用于卫星通信领域，并从中断概率、遍历容量等方面证实理论分析的可行性。 文献［13］在卫星接收机进行连续干扰消除或联合解码的情况下，对采用上行NOMA 的卫星通信系统的性能进行了详细分析，并说明了NOMA 技术在卫星上行通信网络中具有更优的资源利用率和能量效率。 文献［14］在考虑非完美SIC 的情况下，分析了下行NOMA 卫星通信系统的中断概率，并进一步推导了高信噪比条件下系统的高阶中断概率表达式。文献［15］考虑了具有多个地面中继的卫星通信系统，并分析了基于中继选择以及非完美SIC 的中断概率和遍历容量。 文献［16］在用户随机分布的假设下，推导了采用上行NOMA 技术的卫星通信系统遍历容量的闭合表达式。

尽管上述工作都对卫星通信系统中的NOMA技术进行了深入研究，但文献［13－16］只考虑了上行链路或下行链路的传输过程。 在实际应用场景中，卫星通常作为一个空中中继站转发信号，因此对其系统进行精确的分析就需要同时考虑上行和下行链路。 此外，在大规模用户接入场景中，执行SIC 的计算复杂度将随用户数量的增加呈指数增长［17］，将NOMA 技术与传统正交多址技术结合不仅可以有效地降低SIC 解码复杂度，同时还可以通过对功率域与时域、频域或空域等资源的联合利用，进一步提升系统的性能［18－19］。 在这种情况下，本文提出一种采用联合时域-功率域的混合多址接入技术的多用户卫星通信反向链路传输方案，该方案能够充分利用NOMA 技术带来的系统公平性和资源利用率的提高，以及TDMA 技术带来的简单无干扰传输特性［19］，可以进一步提升卫星通信网络的性能。 具体而言，考虑异构用户通信场景，首先将卫星覆盖范围内的多个异构用户分为若干个组，组内用户采用NOMA 技术实现多用户同时传输，组间用户采用TDMA 技术，每个时隙内服务一组用户，通过联合利用时域和频率域资源提升系统性能，相较于现有调度方案［8－9］可以获得更高的频谱效率。 其次，在卫星采用AF 协议的情况下，得到输出信干噪比（Signal-to-Interference-Plus-Noise Ratio， SINR）的表达式；进一步地，在卫星链路服从阴影莱斯分布的条件下，推导出所提混合多址接入技术的卫星系统反向链路遍历容量的闭合表达式；最后，计算机仿真验证了本文所提方案的有效性和优越性，并分析了用户数和信道衰落等参数对系统性能的影响，从而为实际的方案设计和工程应用提供参考。

1 系统模型

本文考虑一个采用混合多址接入技术的卫星通信系统的反向链路传输场景。 如图1 所示，在卫星波束覆盖范围内的2K个异构用户通过卫星R与地球站D进行通信。 由于在NOMA 系统中，多用户信号检测的复杂度随着用户数的增加而极大提高，因此兼顾系统负载和实现复杂性，本文考虑每两个用户一组执行NOMA 传输方案［20］。 根据用户信道差异性将异构用户两两配对，每两个异构用户组成一个用户组，从而将所有用户划分为K个用户组。 组内用户采用NOMA 技术实现多用户同时传输，组间用户采用TDMA 技术，在每个时隙内服务一组用户。 卫星采用AF 协议将接收到的信号转发到地球站D，地球站D采用SIC 技术对各用户信号进行解码，以实现多用户接入和更高的频谱效率。

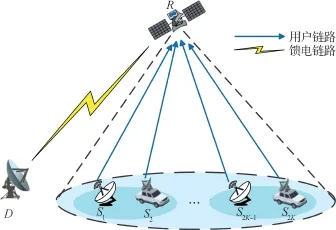
图1 采用混合多址接入技术的卫星通信系统反向链路传输模型

1．1 信道模型

在对卫星信道进行建模时，需要考虑无线信道的衰落特性，以及卫星点波束增益和卫星链路损耗等实际参数的影响［8］，因此信道模型可写成

其中，i∈｛1，2，…，2K，d｝；hi表示卫星链路的信道增益；表示卫星链路的小尺度衰落；Li表示卫星链路的路径损耗，由Friss 传输公式计算得到，即

其中，λ表示载波的波长；di表示卫星与地面用户之间的距离；Gi表示卫星点波束增益，可表示为［21］

与Loo 模型以及Corazza 模型相比，阴影莱斯衰落模型对卫星信道描述的准确性更高，且概率密度函数（Probability Density Function， PDF）的表达式更简单、计算复杂度更低，被广泛用于卫星通信信道建模［16］。 因此，假设用户链路和馈电链路均服从SR 分布的情况下，的PDF 表示为［21］

其 中，，Ωi表示直达径分量的平均功率，2bi表示多径分量的平均功率，mi为Nakagami-m分布的衰落参数，1F1（a；b；z） 为合流超几何参数。 在实际应用时，通常考虑mi取整数的情况，使得性能分析更加简单［23］。 参考文献［24］，可以得到

1．2 信号模型

如图1 所示，在卫星波束覆盖范围内的2K个异构用户被划分为K个用户组，通过卫星R与地球站D进行通信。 组内用户采用NOMA 技术接入卫星，组间用户采用TDMA 技术，每个时隙服务一组用户。 每个时隙内的通信过程包含用户链路和馈电链路两部分。 对于第k个时隙内的NOMA 用户组，在用户链路中，固定终端s1和移动终端s2分别通过信道h1和h2以一定的发射功率［16］将信号x1和x2发送给通信卫星R。 由式（1）至式（4）可知，由于固定终端配备口径更大的反射面天线，相应拥有更高的天线增益，因此信道增益满足｜h1｜2＞｜h2｜2， 卫星R收到的信号表示为

其中，P1和P2表示两用户的发射功率。 在上行NOMA 系统中，倾向于将功率分配给具有较高信道增益的用户，因此两用户的发射功率满足P1＞P2。nR为服从均值为0、方差为的加性高斯白噪声。

在馈电链路中，通信卫星R采用AF 协议，可以保持不同NOMA 用户功率水平之间的差异，以便在地球站进行连续干扰消除检测。 卫星对收到的信号乘 以 一 个 固 定 的 增 益 因 子G ＝后转发给地球站D，地球站的接收信号可表示为

其中，PR为卫星发射功率，hd为卫星R到地球站D的链路信道增益。 地球站在接收到叠加信号之后，根据NOMA 的解码顺序，首先对信道质量更好的用户s1的信号x1进行解码，此时将用户s2的信号x2视为干扰，因此地球站D解码信号x1的输出SINR 表达式为

其次采用SIC 将信号x1从叠加的信号中减去，从而解得信号x2的输出信噪比为

进一步地，地球站D解码信号x1的可达速率表示为

地球站D解码信号x2的可达速率可表示为

由式（12）和式（13）可知，在第k个时隙内，系统的速率表示为

由于卫星共采用K个时隙服务所有的用户，因此系统和速率可表示为

2 遍历容量分析

遍历容量作为衡量一个无线通信系统性能的重要指标，在卫星通信中得到了广泛应用。 基于式（14），本文研究的采用混合多址传输方案的卫星通信系统反向链路的遍历容量可以表示为

首先推导C0的闭合表达式。 由于γ0的PDF 非常复杂，难以直接求得C0的闭合表达式。 因此，首先计算Z ＝z条件下C0｜z的表达式，再取其关于Z的数学期望以求解C0的表达式。 利用矩生成函数（Moment Generating Function，MGF）方法［25］，C0｜z表示为

其中，γ0的条件MGF 可由式（19）计算。

因此，可将C0表示为

为求解式（20）的积分，首先需要得到Z的PDF和Y的累积分布函数（Cumulative Distribution Function， CDF），由定理1 给出。

定理1Z的PDF 表示为

Y的CDF 表示为

其中

A.若A是大气中含量最多的气体,C、D是氧化物且会造成光化学污染,则D转化成C的反应化学方程式为3NO2+H2O==2HNO3+NO

证明：见附录A。

根据Z的PDF 和Y的CDF 求解式（18）中Ι1和Ι2的表达式，由定理2 给出。

定理2Ι1和Ι2的闭合表达式分别为

证明：见附录B。

将式（27）代入式（20）中，C0可表示为

接着将fZ（z） 的计算公式代入式（28），并利用Meijer-G函数的积分公式［26］可得到C0为

接着根据期望的定义，将CZ表示为

根据文献［27］求解式（30）中的积分，可得到CZ的表达式为

最后，将式（17）、式（29）和式（31）代入式（16），即可求出整个卫星通信系统反向链路的遍历容量闭合表达式。

3 计算机仿真与分析

本节通过计算机仿真验证推导出的遍历容量表达式的正确性，并进一步分析用户数和信道衰落等关键参数对系统性能的影响。 同时，为了体现本文所提方案的优越性，与文献［8－9］的传统最优调度和轮询调度方案进行比较。 在卫星链路中，考虑SR分布的两种衰落，分别为轻度阴影衰落（Light Shadowing， LS） 和 平 均 阴 影 衰 落（ Average Shadowing， AS）。 在仿真过程中假设κBT，其中，κ ＝1．38×10－23J／m 表示玻尔兹曼常数。 其他相关仿真参数设置如表1 所示。

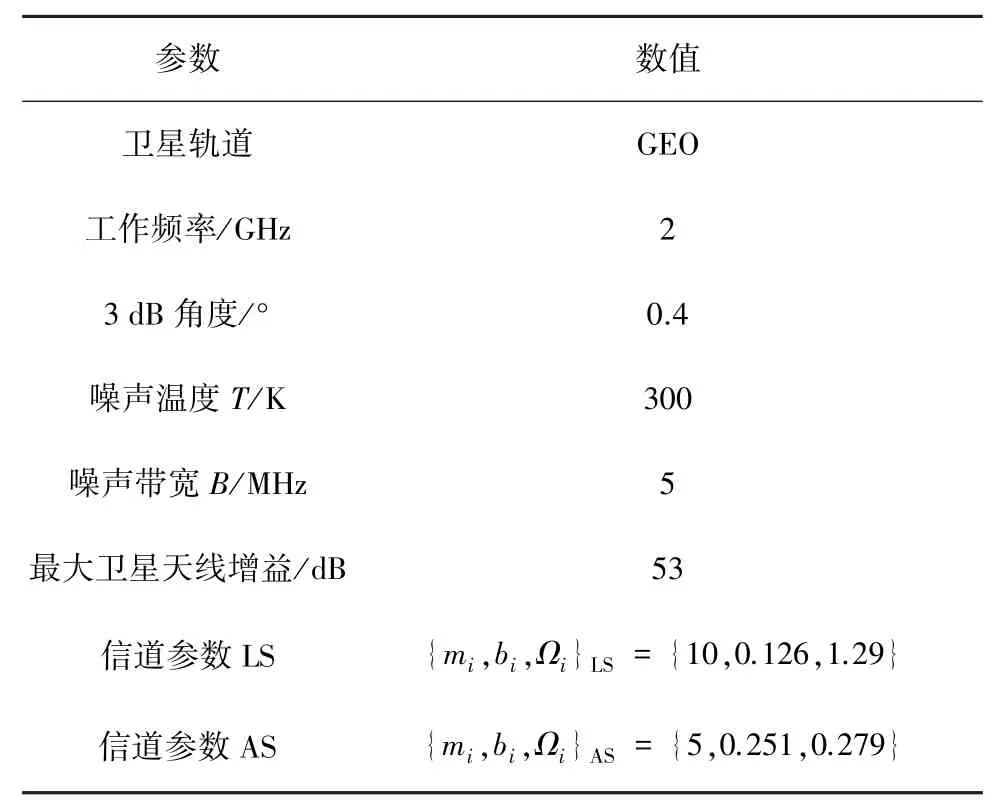
表1 仿真参数设置

图2 给出了遍历容量随用户发射功率的变化曲线，其中卫星发射功率分别取PR ＝40 dBm 和PR ＝50 dBm。 可以看出，闭合表达式得到的结果与蒙特卡罗仿真高度吻合，从而验证了性能分析的正确性。 此外，由图2 还不难发现，当用户链路经历LS 衰落时，系统的遍历容量明显优于经历AS 衰落的情况，这是因为阴影衰落的增加会导致信道质量变差，从而导致系统性能随之恶化。

图2 不同阴影衰落和卫星发射功率下遍历容量随用户发射功率的变化曲线

假设用户最大发射功率分别为PS ＝10 dBm 和PS ＝20 dBm，图3 给出了遍历容量随卫星发射功率变化情况的仿真曲线。 从图3 中可以看出，在用户功率一定的条件下，随着卫星发射功率的增加，系统的遍历容量逐渐增大并最终趋于一个固定的值，这是因为在卫星发射功率增大到一定程度时，系统遍历容量取决于用户链路遍历容量。

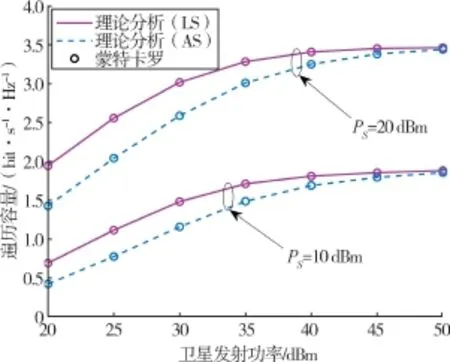
图3 不同阴影衰落和用户发射功率下遍历容量随卫星发射功率的变化曲线

图4 对比了分别采用两种不同传输方案下的系统遍历容量随用户发射功率的变化情况。 可以看出，系统遍历容量均随着发射功率的增加而增大，但本文所提出的混合多址接入方案明显优于文献［8－9］中采用传统轮询调度和最优调度的方案，从而验证了本文提出的传输方案在卫星通信系统中的优越性。

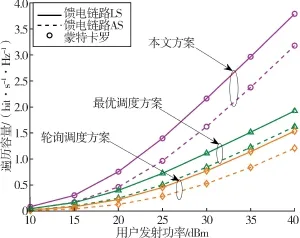
图4 不同阴影衰落和用户调度方案下遍历容量随用户发射功率的变化曲线

图5 分析了在采用不同的传输方案下，用户数对系统遍历容量的影响。 可以看出，在3 种传输方案中，随着用户数的增多，系统遍历容量均有所提高，而本文所提出的方案始终优于文献［8－9］中采用传统轮询调度和最优调度的方案。

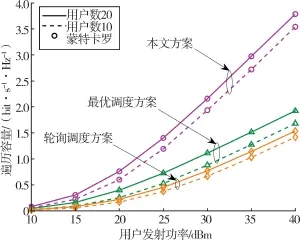
图5 不同用户数和用户调度方案下遍历容量随用户发射功率的变化曲线

4 结束语

本文提出了一种采用联合时域-功率域的混合多址接入技术的卫星系统传输方案，并对其反向链路的遍历容量进行分析。 首先对卫星波束覆盖范围内的所有异构用户进行用户分组，组内用户采用NOMA 技术接入卫星，组间用户采用TDMA 技术，每个时隙内服务一组用户，并在卫星采用AF 协议的条件下得到输出信干噪比的表达式；其次，假设卫星链路服从阴影莱斯分布，推导整个卫星通信系统反向链路的遍历容量的闭合表达式；最后，通过计算机仿真验证了理论分析的正确性以及本文所提出传输方案相比现有方案的优越性，并分析了用户数和信道衰落等关键参数对系统性能的影响，可以为实际卫星通信系统的设计和工程应用提供参考。

附录A

在用户链路和馈电链路中，利用式（7），γi ＝的PDF 可表示为

其中，1F1（a，b，z） 为合流超几何函数，将其展开后得［26］

其中

已知

将式（附A5）代入式（附A6）并积分，可得到关于Λ的最终表达式为

其中

附录B

根据式（20），C0中的积分Ι1表示为

参考文献［26］，可得Ι1为

接下来，将Ι1的表达式代入C1的计算公式中，可将C1中的积分Ι2表示为

可将式（附B3）转换为包含Meijer-G函数积分的形式［28］

参考文献［26］，可得Ι2为